发帖
雷达卡
在锂电池中，锂枝晶的生长行为如同难以驯服的野草，一旦失控便可能穿透隔膜引发短路。为了精准捕捉这种复杂晶体的演化过程，相场模型成为研究者手中的核心工具——它无需显式追踪界面变化，而是通过相场变量与离子浓度场之间的耦合关系，即可再现分形结构的动态生长。
相场模拟的核心在于两个关键方程的协同作用：一个是描述相界面演化的相场变量φ方程，另一个是反映锂离子扩散行为的浓度c方程。其中，φ的演化方程可表示为：
% 相场演化方程（伪代码）
epsilon^2 * laplacian(phi) + phi*(1-phi)*(phi-0.5 + m*delta_c) = tau * dphi_dt该公式中的epsilon参数控制着界面过渡区的宽度，tau代表弛豫时间，而delta_c则体现浓度差异带来的驱动力。虽然整体形式类似标准双阱势函数的扩展版本，但引入驱动项后对数值稳定性要求极高。若epsilon取值过大，界面将变得模糊不清；过小则会导致计算量剧增，求解耗时显著上升。
在COMSOL软件中实施此类模型时，首先需通过“模型向导”选择合适的PDE物理场模块。随后进入自定义偏微分方程设置环节：
% COMSOL PDE系数形式设置（节选）
c_coeff = epsilon^2
f = phi*(1-phi)*(phi-0.5 + m*(c - c_eq))
da_coeff = tau这里存在一个关键技巧：应将非线性项置于f项而非源项位置，以便软件自动构建雅可比矩阵，提升收敛效率。然而许多初学者常忽略启用“非线性求解器”，导致仿真结果异常——例如生成出笔直如线的假性枝晶，完全丧失真实分形特征，造成严重误判。
边界条件的设定同样至关重要。在电极表面通常采用通量型边界条件：
n·grad(c) = -J0 * exp(alpha*F*eta/(R*T)) % 巴特勒-福尔默动力学该表达式中的指数项极易引发数值不稳定。曾有案例显示，当交换电流密度J0被误设高出两个数量级时，浓度场迅速发散，最终可视化结果呈现出类似抽象艺术的画面，实为计算崩溃的表现。
关于网格划分，推荐使用自适应网格策略。由于枝晶尖端曲率半径可低至纳米尺度，固定网格难以兼顾精度与效率。一种高效做法是：先在较粗网格下完成初步演化，获得大致形态后，将其作为初始场导入精细网格继续计算，此方法可节省约30%的总体算力消耗。
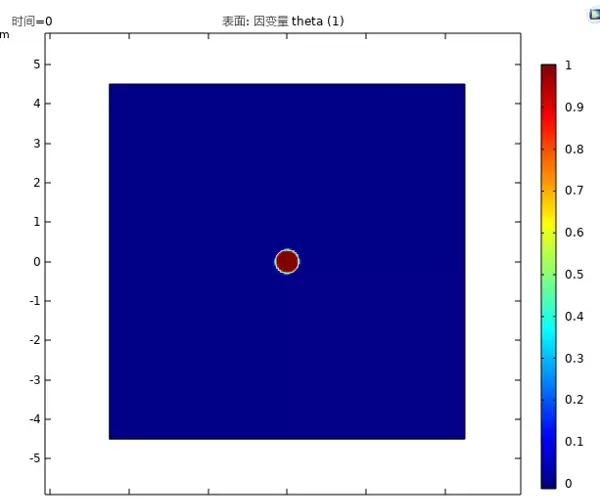
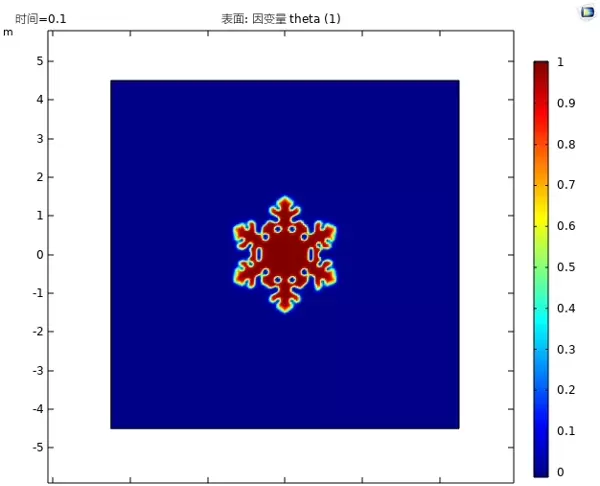
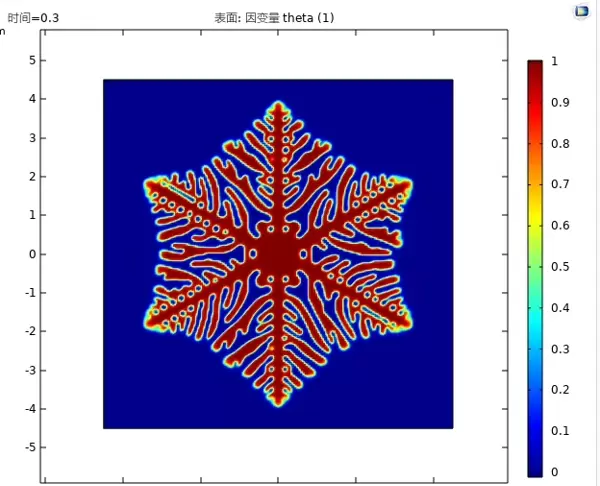
以下展示一组典型仿真输出（配图示意）：枝晶呈现海藻状多级分叉结构，其尖端区域伴随明显的电场集中现象，以红色高亮标识。此类模拟能够清晰揭示不同电流密度下的生长模式差异——低电流条件下形成羽毛状分形结构，而在高电流下则转变为密集针状突起，与实验中观测到的SEM图像高度吻合。
调试此类模型的过程犹如照料电子宠物，必须持续监控求解器的收敛状态。经验丰富的用户往往会在日志文件中设置预警机制：一旦残差曲线出现高频振荡，提示界面参数可能需要重新调整；若浓度场出现负值，则极有可能是通量边界的符号输入错误，需立即核查修正。
京公网安备 11010802022788号
