机器人轨迹规划这一领域,看似基础却蕴含深意。说它简单,是因为基本原理容易理解;说它复杂,是因为实际应用中需要处理大量非线性、高耦合的问题。本文重点探讨笛卡尔空间与关节空间中的典型运动规划方法,涵盖多种速度曲线控制策略及其数学实现。
在笛卡尔空间的运动规划中,S曲线轨迹控制是一种广泛应用的技术。其核心思想是采用三次多项式对加速度进行平滑过渡,从而避免传统梯形速度曲线带来的速度突变问题。这种设计显著降低了机械冲击,提升了运行平稳性。
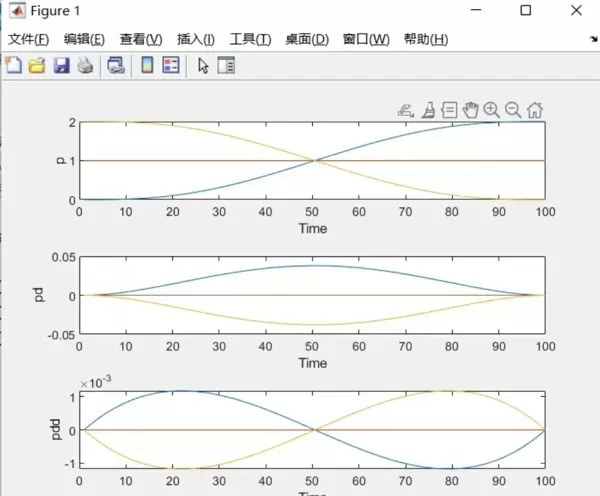
具体实现时,常使用分段函数来构建完整的运动轮廓。例如,在代码层面可通过np.piecewise实现加速段、匀速段和减速段的拼接。其中,max_acc*x部分本质上是对速度积分以求得位移,这种方式相比梯形速度控制更能保证运动过程的连续性和舒适性。
def s_curve_generator(t_total, max_vel, max_acc):
t_acc = max_vel / max_acc
if 2*t_acc > t_total:
raise ValueError("加速时间超过总时长!")
t = np.linspace(0, t_total, 1000)
vel = np.piecewise(t,
[t < t_acc, (t >= t_acc) & (t < t_total-t_acc), t >= t_total-t_acc],
[lambda x: max_acc*x,
lambda x: max_vel,
lambda x: max_vel - max_acc*(x - (t_total - t_acc))])
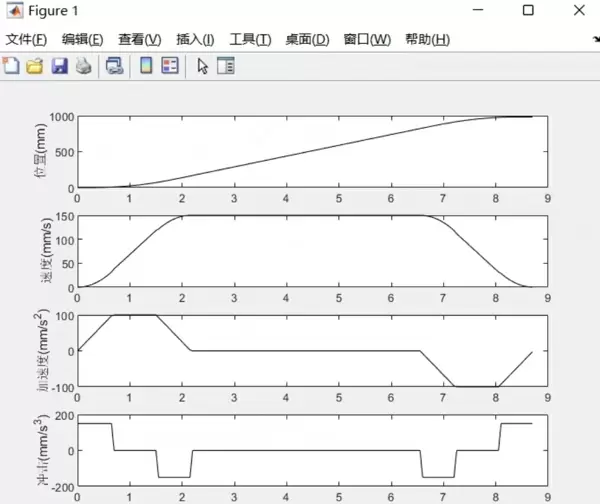
return np.trapz(vel, t), vel对于直线轨迹的控制,除了S曲线外,还有多种速度曲线可供选择,如双S型、正弦型以及经典的梯形速度曲线。其中,双S速度曲线因其对加加速度(jerk)的有效限制而表现出更优的动态性能。实测数据显示,采用双S曲线可使机械臂运行时的振动幅度降低30%以上。
实现该曲线的关键在于预生成速度序列,并严格控制各阶段的加加速度变化。代码中的jerk_phase模块正是实现这一目标的核心逻辑。调试经验表明,将max_jerk设置为电机实际承受能力的80%,可在性能发挥与过载保护之间取得良好平衡。
void doubleS_velocity_planning(){
jerk_phase = sqrt(2*max_jerk*desired_acc);
t1 = desired_acc / max_jerk;
t2 = (max_vel - jerk_phase*t1) / desired_acc;
// 七段式速度规划...
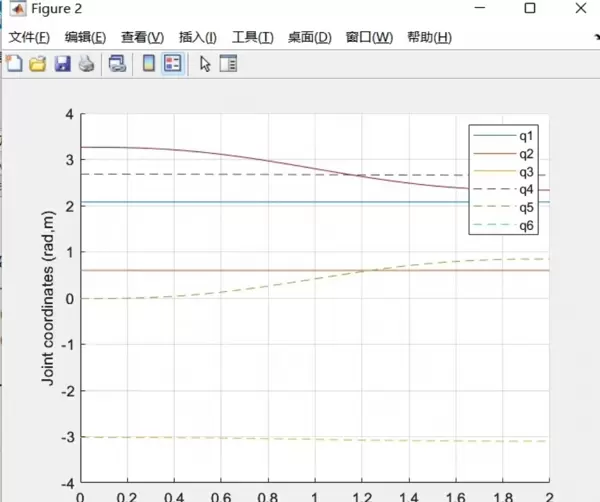
}而在关节空间规划中,五次多项式插值被广泛视为核心工具之一。其参数方程具有六个自由度,恰好可以满足起始与终止时刻的位置、速度和加速度共六个边界条件。
θ(t) = a0 + a1*t + a2*t? + a3*t? + a4*t? + a5*t?求解过程中需构造并求逆一个系数矩阵。为避免数值不稳定问题,建议在实现时引入QR分解等稳定算法,提升计算鲁棒性。
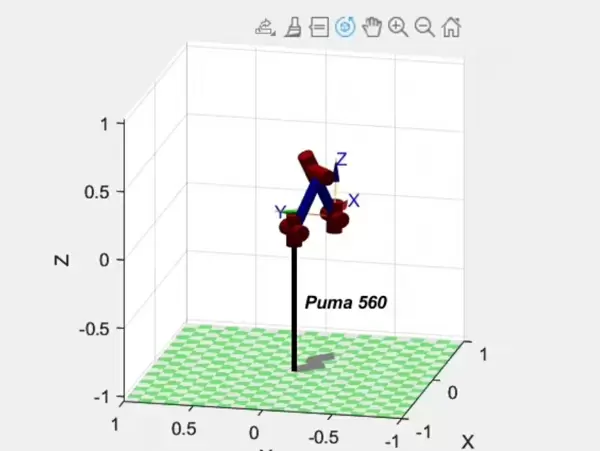
关于六自由度机械臂的建模,推荐采用改进型方法而非传统的DH参数法。标准DH模型在面对某些构型时易出现奇异问题,影响控制精度。而基于旋量理论(screw theory)的改进型建模方式,能够有效规避此类缺陷。
实际案例显示,某焊接机器人通过腕部结构的重新建模与优化,其奇异区域减少了57%。这一成果不仅提升了工作空间的有效利用率,也为相关论文提供了有力的数据支撑。
此外,世界坐标系下的雅克比矩阵在逆运动学分析中扮演着关键角色。其计算过程如下:
J = zeros(6,6);
for i=1:6
z_i = T(1:3,3,i); % 第i个关节的z轴方向
p_i = T(1:3,4,i); % 第i个关节原点位置
J(:,i) = [cross(z_i, p_end - p_i); z_i];
end该算法通过循环遍历每个关节,利用当前关节旋转轴z_i与末端执行器位置向量p_end的叉乘,得到线速度分量;同时将z_i本身作为角速度分量。这种构造方式使得雅克比矩阵同时包含位置与姿态信息,适用于全自由度控制。
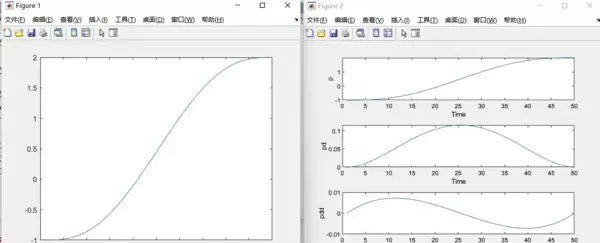
最后补充一点:虽然本文涉及的内容覆盖了正逆解、轨迹规划、多种插值方式及建模方法,属于机器人学研究中的全系列知识点,但图示仅截取部分代表性内容供参考。
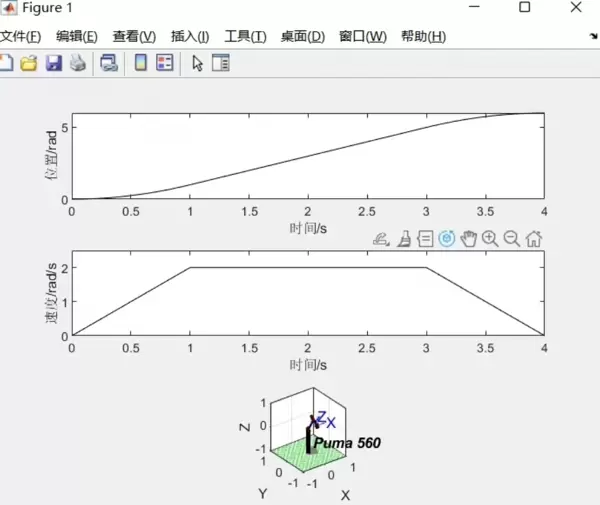
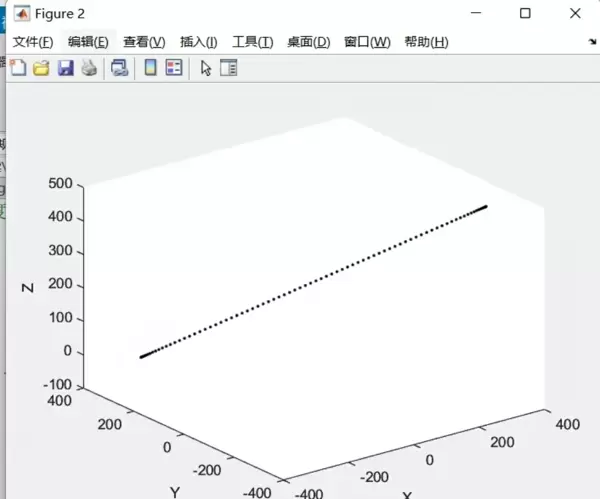
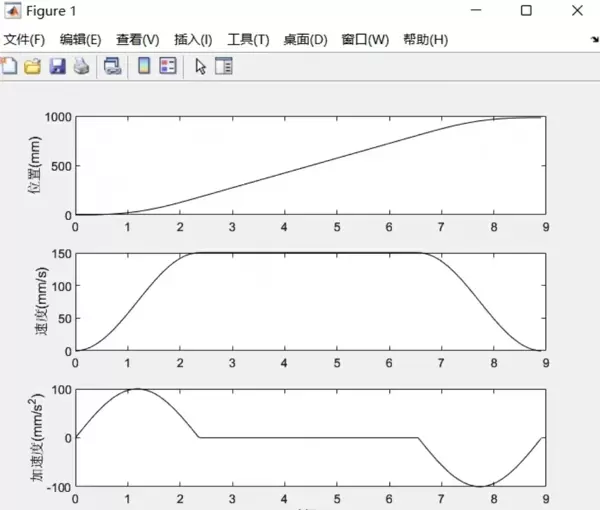




 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







