数据挖掘之决策树、ID3算法

是 否 +2 论坛币

k人 参与回答

经管之家送您一份

应届毕业生专属福利!

求职就业群

赵安豆老师微信：zhaoandou666

经管之家联合CDA

送您一个全额奖学金名额~ !

立即领取

感谢您参与论坛问题回答

经管之家送您两个论坛币！

+2 论坛币

一、决策树

1. 基本概念

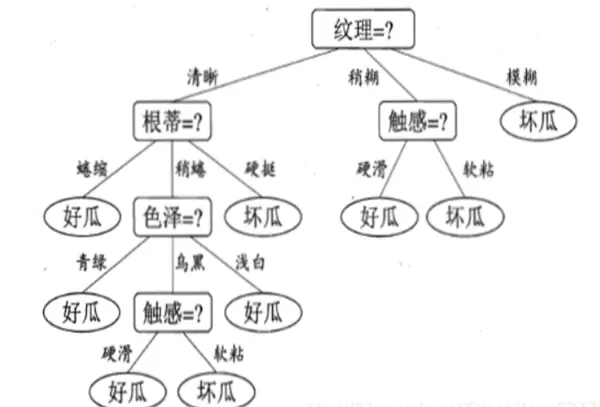
决策树是一种基于树形结构的机器学习模型，用于分类或回归任务。它通过从根节点到叶节点的路径表达一系列决策规则。其中，根节点通常代表对分类结果影响最大的特征，而叶节点则表示最终的分类输出。

其核心目标是：在每一次分裂过程中，选择能够使子节点比父节点“更纯”的特征进行划分，从而逐步提升分类的准确性。

2. 纯度与信息熵

纯度 指的是一个数据集合中类别一致的程度。例如，若某个集合中的所有样本都属于同一类别（如全部为“苹果”），则该集合具有很高的纯度。

信息熵 是衡量集合不确定性的指标，反映了为了确定样本类别所需要的平均信息量。熵值越低，说明集合越纯净。

信息增益 则定义为划分前的信息熵减去划分后各子集加权平均的信息熵。该值越大，说明此次划分带来的纯度提升越明显。

3. ID3 算法原理

ID3算法利用信息增益作为特征选择的标准。具体做法是：计算每个特征的信息增益，选择增益最大者作为当前节点的分裂属性，递归地构建整棵决策树。

其核心公式如下：

该公式的含义是：用父节点的熵减去其所有子节点熵的加权和，权重为子集占父集的比例。所得差值即为信息增益。

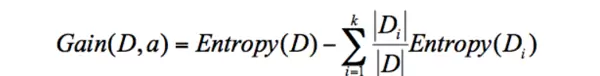
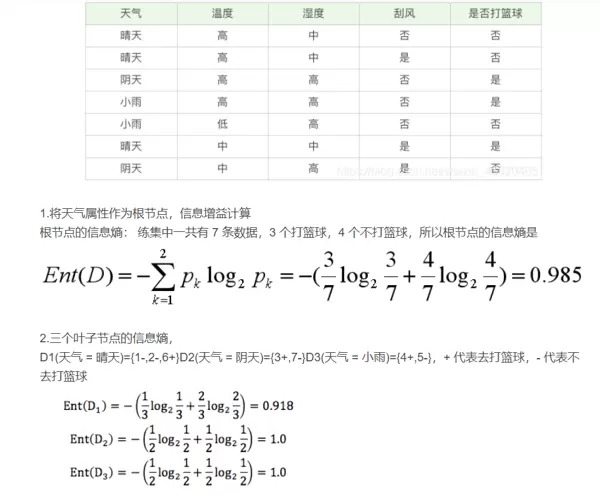
案例说明

通过实际数据示例可以更直观理解ID3的工作方式：

算法局限性分析

ID3算法存在一个显著缺陷：它倾向于选择取值较多的特征作为分裂节点。这可能导致生成的树结构不合理，甚至过拟合。

举例来说，假设使用“身份证号”这一属性进行分类。由于每个人的身份证号唯一，每个子集往往只包含单一样本：

姓名	身份证	是否考研
张三	123345678	是
李四	456789094	否
张三	345678900	否

以身份证号“123345678”为例，对应的子集仅含一个结果：“是”。此时，p(是)=1，p(否)=0，代入信息熵公式：

熵 = -(1×log1 + 0×log0) = 0（此为简化示例，忽略0×log0的极限处理）

由于每个子集的熵接近于0，整体加权熵极小，导致信息增益异常高，从而使身份证号可能被误选为根节点，显然不具备泛化能力。

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

分享0 收藏0 回帖

关键词：数据挖掘 决策树 身份证号 举例来说 机器学习