# 导入核心数据处理库
import numpy as np # 用于数值计算(对数变换、数组操作、误差计算)
import pandas as pd # 用于数据读取、清洗、特征工程
# 读取保险数据集(CSV格式,默认逗号分隔)
# 数据集包含:年龄(age)、性别(sex)、BMI指数(bmi)、子女数(children)、是否吸烟(smoker)、地区(region)、保险费用(charges)
data = pd.read_csv('./data/insurance.csv')
# 查看前5行数据,快速了解数据结构(列名、数据类型、样本取值)
print("原始数据集前5行:")
print(data.head())
print("-" * 50)
# # EDA(探索性数据分析):分析目标变量分布及各特征对保费的影响
# 导入绘图库
import matplotlib.pyplot as plt
import seaborn as sns # 基于matplotlib的高级绘图库,更适合统计可视化
# 设置中文显示(解决图表中文乱码问题,适配PyCharm)
plt.rcParams['font.sans-serif'] = ['SimHei'] # Windows系统
# plt.rcParams['font.sans-serif'] = ['Arial Unicode MS'] # Mac系统
plt.rcParams['axes.unicode_minus'] = False # 解决负号显示异常
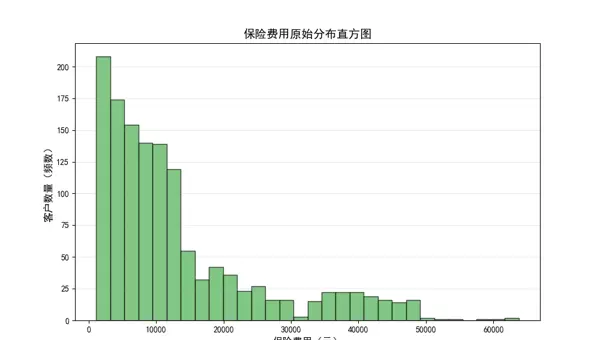
# -------------------------- 1. 目标变量(保险费用)原始分布 --------------------------
plt.figure(figsize=(10, 6))
plt.hist(data['charges'], bins=30, edgecolor='black', alpha=0.7, color='#4CAF50')
plt.title('保险费用原始分布直方图', fontsize=14, fontweight='bold')
plt.xlabel('保险费用(元)', fontsize=12)
plt.ylabel('客户数量(频数)', fontsize=12)
plt.grid(axis='y', alpha=0.3) # 添加水平网格线,提升可读性
plt.show() # PyCharm中需调用show()显示图表
# 观察结论:保费呈明显右偏分布(多数客户保费较低,少数高风险客户保费极高)
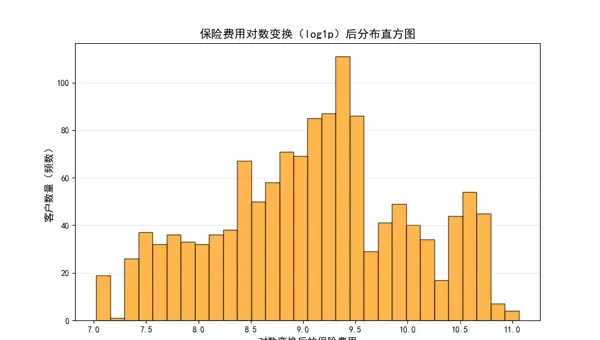
# -------------------------- 2. 目标变量对数变换后分布 --------------------------
plt.figure(figsize=(10, 6))
# np.log1p = log(1+x),避免x=0时log(0)的无穷大问题,且逆变换可逆(expm1)
plt.hist(np.log1p(data['charges']), bins=30, edgecolor='black', alpha=0.7, color='#FF9800')
plt.title('保险费用对数变换(log1p)后分布直方图', fontsize=14, fontweight='bold')
plt.xlabel('对数变换后的保险费用', fontsize=12)
plt.ylabel('客户数量(频数)', fontsize=12)
plt.grid(axis='y', alpha=0.3)
plt.show()
# 观察结论:对数变换后分布更接近正态分布,可提升模型预测精度
# -------------------------- 3. 性别(sex)对保费的影响 --------------------------
plt.figure(figsize=(10, 6))
# 核密度图(KDE):展示不同性别的保费概率分布
sns.kdeplot(data.loc[data.sex == 'male', 'charges'], shade=True, label='男性', color='#2196F3')
sns.kdeplot(data.loc[data.sex == 'female', 'charges'], shade=True, label='女性', color='#E91E63')
plt.title('不同性别的保险费用分布对比', fontsize=14, fontweight='bold')
plt.xlabel('保险费用(元)', fontsize=12)
plt.ylabel('概率密度', fontsize=12)
plt.legend(fontsize=11)
plt.grid(alpha=0.3)
plt.show()
# 观察结论:男女保费分布差异极小,性别对保费影响不显著
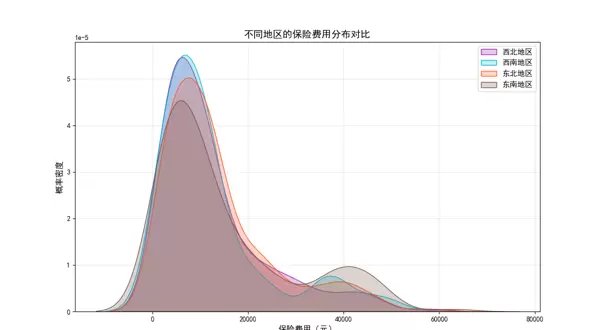
# -------------------------- 4. 地区(region)对保费的影响 --------------------------
plt.figure(figsize=(12, 7))
sns.kdeplot(data.loc[data.region == 'northwest', 'charges'], shade=True, label='西北地区', color='#9C27B0')
sns.kdeplot(data.loc[data.region == 'southwest', 'charges'], shade=True, label='西南地区', color='#00BCD4')
sns.kdeplot(data.loc[data.region == 'northeast', 'charges'], shade=True, label='东北地区', color='#FF5722')
sns.kdeplot(data.loc[data.region == 'southeast', 'charges'], shade=True, label='东南地区', color='#795548')
plt.title('不同地区的保险费用分布对比', fontsize=14, fontweight='bold')
plt.xlabel('保险费用(元)', fontsize=12)
plt.ylabel('概率密度', fontsize=12)
plt.legend(fontsize=11)
plt.grid(alpha=0.3)
plt.show()
# 观察结论:四个地区的保费分布重叠度高,地区对保费影响较弱
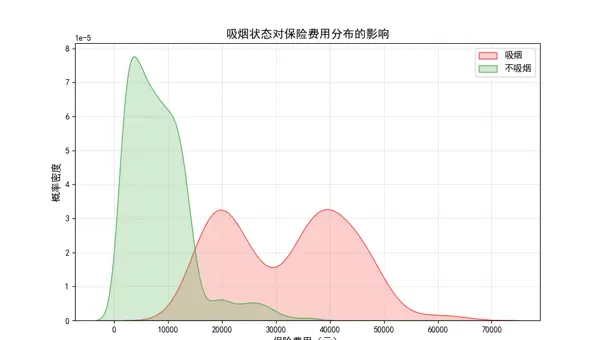
# -------------------------- 5. 是否吸烟(smoker)对保费的影响 --------------------------
plt.figure(figsize=(10, 6))
sns.kdeplot(data.loc[data.smoker == 'yes', 'charges'], shade=True, label='吸烟', color='#F44336')
sns.kdeplot(data.loc[data.smoker == 'no', 'charges'], shade=True, label='不吸烟', color='#4CAF50')
plt.title('吸烟状态对保险费用分布的影响', fontsize=14, fontweight='bold')
plt.xlabel('保险费用(元)', fontsize=12)
plt.ylabel('概率密度', fontsize=12)
plt.legend(fontsize=11)
plt.grid(alpha=0.3)
plt.show()
# 观察结论:吸烟客户的保费显著高于不吸烟客户,是保费的关键影响因素
# -------------------------- 6. 子女数(children)对保费的影响 --------------------------
plt.figure(figsize=(12, 7))
# 分别绘制0-5个子女的保费分布
sns.kdeplot(data.loc[data.children == 0, 'charges'], shade=True, label='0个子女', color='#3F51B5')
sns.kdeplot(data.loc[data.children == 1, 'charges'], shade=True, label='1个子女', color='#2196F3')
sns.kdeplot(data.loc[data.children == 2, 'charges'], shade=True, label='2个子女', color='#00BCD4')
sns.kdeplot(data.loc[data.children == 3, 'charges'], shade=True, label='3个子女', color='#4CAF50')
sns.kdeplot(data.loc[data.children == 4, 'charges'], shade=True, label='4个子女', color='#FFC107')
sns.kdeplot(data.loc[data.children == 5, 'charges'], shade=True, label='5个子女', color='#FF9800')
plt.title('不同子女数的保险费用分布对比', fontsize=14, fontweight='bold')
plt.xlabel('保险费用(元)', fontsize=12)
plt.ylabel('概率密度', fontsize=12)
plt.legend(fontsize=10)
plt.grid(alpha=0.3)
plt.show()
# 观察结论:子女数对保费有一定影响,但差异不如吸烟状态显著
# # 特征工程:简化特征维度、转换特征类型、编码分类变量
# -------------------------- 1. 删除弱影响特征 --------------------------
# 基于EDA结论:性别(sex)和地区(region)对保费影响极小,删除以简化模型
data = data.drop(['region', 'sex'], axis=1)
print("删除弱影响特征后的数据集前5行:")
print(data.head())
print("-" * 50)
# -------------------------- 2. 特征离散化:连续/多分类特征转为二分类 --------------------------
def feature_discretize(df, bmi_threshold, child_threshold):
"""
自定义函数:将连续特征BMI和多分类特征子女数离散化为二分类
参数:
df: 每行数据(apply按行处理)
bmi_threshold: BMI分类阈值(这里30是肥胖标准)
child_threshold: 子女数分类阈值(这里0区分"无子女"和"有子女")
返回:
处理后的单行数据
"""
# BMI≥30标记为"over"(肥胖),否则为"under"(非肥胖)
df['bmi'] = 'over' if df['bmi'] >= bmi_threshold else 'under'
# 子女数==0标记为"no"(无子女),否则为"yes"(有子女)
df['children'] = 'no' if df['children'] == child_threshold else 'yes'
return df
# 按行应用离散化函数,指定BMI阈值30、子女数阈值0
data = data.apply(feature_discretize, axis=1, args=(30, 0))
print("特征离散化后的数据集前5行:")
print(data.head())
print("-" * 50)
# -------------------------- 3. 分类变量独热编码(One-Hot Encoding) --------------------------
# 离散化后的特征(bmi、children、smoker)均为分类变量,需编码为模型可识别的数值
data = pd.get_dummies(data, drop_first=False) # drop_first=False:保留所有分类(避免信息丢失)
print("独热编码后的数据集前5行:")
print(data.head())
print("-" * 50)
# -------------------------- 4. 分离特征矩阵(X)和目标变量(y) --------------------------
X = data.drop('charges', axis=1) # X:所有输入特征(排除目标变量)
y = data['charges'] # y:目标变量(需预测的保险费用)
# -------------------------- 5. 缺失值填充 --------------------------
# 假设缺失值为"无该特征",用0填充(实际项目可根据特征含义优化,如均值/中位数)
X.fillna(0, inplace=True)
y.fillna(0, inplace=True)
print("最终特征矩阵前5行:")
print(X.head())
print("-" * 50)
# # 模型训练:划分数据集、构造多项式特征、训练三种回归模型
# -------------------------- 1. 划分训练集和测试集 --------------------------
from sklearn.model_selection import train_test_split
# test_size=0.3:30%数据为测试集(评估泛化能力),70%为训练集(训练参数)
# random_state=42:固定随机种子,保证结果可复现(原代码未设置,补充优化)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# -------------------------- 2. 构造多项式特征(捕捉非线性关系) --------------------------
from sklearn.preprocessing import PolynomialFeatures
# degree=2:构造二次多项式特征(含特征平方项和交叉项)
# include_bias=False:不添加偏置项(模型会自动处理截距)
poly_features = PolynomialFeatures(degree=2, include_bias=False)
X_train_poly = poly_features.fit_transform(X_train) # 训练集:拟合+转换(仅用训练集数据,避免泄露)
# 原代码错误:测试集用了fit_transform(会重新拟合测试集数据,导致数据泄露),修正为transform
X_test_poly = poly_features.transform(X_test) # 测试集:仅转换(复用训练集的多项式规则)
print(f"多项式特征构造后:训练集维度 {X_train_poly.shape},测试集维度 {X_test_poly.shape}")
print("-" * 50)
# -------------------------- 3. 导入三种回归模型 --------------------------
from sklearn.linear_model import LinearRegression # 普通线性回归(基准模型)
from sklearn.linear_model import Ridge # 岭回归(L2正则化,缓解过拟合)
from sklearn.ensemble import GradientBoostingRegressor # 梯度提升回归(集成学习,捕捉复杂关系)
# -------------------------- 4. 训练普通线性回归 --------------------------
reg = LinearRegression()
# 用对数变换后的目标变量训练(修正右偏分布,提升模型效果)
reg.fit(X_train_poly, np.log1p(y_train))
# 补充原代码缺失的测试集预测(原代码未定义y_predict,导致评估报错)
y_predict = reg.predict(X_test_poly)
# -------------------------- 5. 训练岭回归 --------------------------
ridge = Ridge(alpha=1.0) # alpha:正则化强度(默认1.0,可通过调参优化)
ridge.fit(X_train_poly, np.log1p(y_train))
y_predict_ridge = ridge.predict(X_test_poly)
# -------------------------- 6. 训练梯度提升回归 --------------------------
booster = GradientBoostingRegressor(random_state=42) # random_state保证可复现
booster.fit(X_train_poly, np.log1p(y_train))
y_predict_boost = booster.predict(X_test_poly)
# # 模型评估:使用RMSE(均方根误差)评估性能
# RMSE越小,预测精度越高;对比训练集/测试集RMSE,判断过拟合/欠拟合
from sklearn.metrics import mean_squared_error
# 定义评估函数:统一计算对数尺度和原始尺度的RMSE(避免重复代码)
def evaluate_model(model_name, y_train_true, y_train_pred, y_test_true, y_test_pred):
"""
计算模型的RMSE评估指标
参数:
model_name: 模型名称(用于打印)
y_train_true: 训练集真实值(原始尺度)
y_train_pred: 训练集预测值(对数尺度)
y_test_true: 测试集真实值(原始尺度)
y_test_pred: 测试集预测值(对数尺度)
返回:
对数尺度训练/测试RMSE、原始尺度训练/测试RMSE
"""
# 对数尺度RMSE(反映相对误差,不受数据尺度影响)
log_rmse_train = np.sqrt(mean_squared_error(y_true=np.log1p(y_train_true), y_pred=y_train_pred))
log_rmse_test = np.sqrt(mean_squared_error(y_true=np.log1p(y_test_true), y_pred=y_test_pred))
# 原始尺度RMSE(反映绝对误差,单位为元,更直观)
# 用expm1逆转log1p变换(避免直接exp导致的误差:exp(log1p(x))=x+1)
rmse_train = np.sqrt(mean_squared_error(y_true=y_train_true, y_pred=np.expm1(y_train_pred)))
rmse_test = np.sqrt(mean_squared_error(y_true=y_test_true, y_pred=np.expm1(y_test_pred)))
# 格式化输出结果
print("=" * 60)
print(f"{model_name} 评估结果:")
print(f"对数尺度 - 训练集RMSE:{log_rmse_train:.4f} | 测试集RMSE:{log_rmse_test:.4f}")
print(f"原始尺度 - 训练集RMSE:{rmse_train:.2f} 元 | 测试集RMSE:{rmse_test:.2f} 元")
print("=" * 60 + "\n")
return log_rmse_train, log_rmse_test, rmse_train, rmse_test
# -------------------------- 1. 评估普通线性回归 --------------------------
evaluate_model(
model_name="普通线性回归(二次多项式特征)",
y_train_true=y_train,
y_train_pred=reg.predict(X_train_poly),
y_test_true=y_test,
y_test_pred=y_predict
)
# -------------------------- 2. 评估岭回归 --------------------------
evaluate_model(
model_name="岭回归(L2正则化+二次多项式特征)",
y_train_true=y_train,
y_train_pred=ridge.predict(X_train_poly),
y_test_true=y_test,
y_test_pred=y_predict_ridge
)
# -------------------------- 3. 评估梯度提升回归 --------------------------
evaluate_model(
model_name="梯度提升回归(集成学习+二次多项式特征)",
y_train_true=y_train,
y_train_pred=booster.predict(X_train_poly),
y_test_true=y_test,
y_test_pred=y_predict_boost
)
运行结果:


'''
原始数据集前5行:
age sex bmi children smoker region charges
0 19 female 27.900 0 yes southwest 16884.92400
1 18 male 33.770 1 no southeast 1725.55230
2 28 male 33.000 3 no southeast 4449.46200
3 33 male 22.705 0 no northwest 21984.47061
4 32 male 28.880 0 no northwest 3866.85520
--------------------------------------------------
删除弱影响特征后的数据集前5行:
age bmi children smoker charges
0 19 27.900 0 yes 16884.92400
1 18 33.770 1 no 1725.55230
2 28 33.000 3 no 4449.46200
3 33 22.705 0 no 21984.47061
4 32 28.880 0 no 3866.85520
--------------------------------------------------
特征离散化后的数据集前5行:
age bmi children smoker charges
0 19 under no yes 16884.92400
1 18 over yes no 1725.55230
2 28 over yes no 4449.46200
3 33 under no no 21984.47061
4 32 under no no 3866.85520
--------------------------------------------------
独热编码后的数据集前5行:
age charges bmi_over ... children_yes smoker_no smoker_yes
0 19 16884.92400 0 ... 0 0 1
1 18 1725.55230 1 ... 1 1 0
2 28 4449.46200 1 ... 1 1 0
3 33 21984.47061 0 ... 0 1 0
4 32 3866.85520 0 ... 0 1 0
[5 rows x 8 columns]
--------------------------------------------------
最终特征矩阵前5行:
age bmi_over bmi_under children_no children_yes smoker_no smoker_yes
0 19 0 1 1 0 0 1
1 18 1 0 0 1 1 0
2 28 1 0 0 1 1 0
3 33 0 1 1 0 1 0
4 32 0 1 1 0 1 0
--------------------------------------------------
多项式特征构造后:训练集维度 (936, 35),测试集维度 (402, 35)
--------------------------------------------------
============================================================
普通线性回归(二次多项式特征) 评估结果:
对数尺度 - 训练集RMSE:0.3825 | 测试集RMSE:0.3740
原始尺度 - 训练集RMSE:4707.56 元 | 测试集RMSE:4523.22 元
============================================================
============================================================
岭回归(L2正则化+二次多项式特征) 评估结果:
对数尺度 - 训练集RMSE:0.3825 | 测试集RMSE:0.3740
原始尺度 - 训练集RMSE:4710.78 元 | 测试集RMSE:4523.84 元
============================================================
============================================================
梯度提升回归(集成学习+二次多项式特征) 评估结果:
对数尺度 - 训练集RMSE:0.3506 | 测试集RMSE:0.3988
原始尺度 - 训练集RMSE:4279.33 元 | 测试集RMSE:4599.79 元
============================================================
进程已结束,退出代码为 0
'''










 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







