发帖
雷达卡
在计算机科学中，“图”是一个常见的概念，尤其在数据结构领域有着广泛的应用。提到图，自然离不开图论（Graph Theory），它是数学的一个分支，专门研究以图为对象的结构与性质。图论中的“图”由若干个点以及连接这些点的线组成，用于描述事物之间的特定关系——其中点代表实体，线则表示两个实体之间存在某种关联。
你可能会好奇：这和线性代数、矩阵有什么联系？接下来我们就通过具体的数学定义和实际应用来揭示它们之间的紧密关系。
图的数学定义
从数学角度出发，一个图 $ G $ 被定义为一个有序三元组 $ (V, E, \phi) $：
- $ V $ 是非空的顶点集合；
- $ E $ 是边的集合，且不与 $ V $ 相交；
- $ \phi $ 是关联函数，将每条边映射到一对无序的顶点上。
若边 $ e $ 满足 $ \phi(e) = uv $，则称 $ e $ 连接顶点 $ u $ 和 $ v $，而 $ u $、$ v $ 即为该边的端点。这一定义为我们后续结合矩阵工具分析图结构打下了理论基础。
邻接矩阵的实际应用
为了将图转化为可计算的形式，我们可以使用邻接矩阵（Adjacency Matrix）来表示顶点间的连接关系。设图 $ G $ 有 $ n $ 个顶点 $ v_1, v_2, \ldots, v_n $，其邻接矩阵 $ A = (a_{ij})_{n×n} $ 定义如下：
当顶点 $ i $ 与顶点 $ j $ 之间存在边时，$ a_{ij} = 1 $；否则为 0。若允许自环（即节点连接自身），则对角线元素也可能为1。
下面我们通过一个经典案例来看如何运用邻接矩阵解决现实问题——源自1994年全国大学生数学建模竞赛B题的锁具设计问题。
某厂生产的弹子锁具，每把钥匙有5个槽，每个槽的高度可在集合 {1,2,3,4,5,6} 中选取。但由于工艺限制，需满足以下两个条件：
- 五个槽的高度中至少出现3个不同的数值；
- 相邻两槽的高度差不能等于5（即不能出现1与6相邻的情况）。
符合上述条件的所有不同锁具构成一批产品。销售时，每60个随机选取的锁具装成一箱出售。问题是：每批共有多少个锁具？能装多少箱？
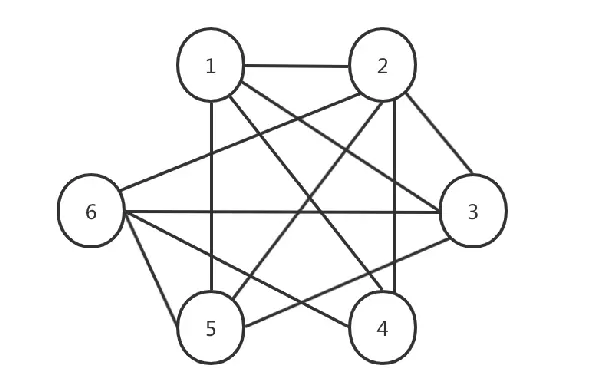
要解答这个问题，直接枚举所有组合会非常繁琐。但借助图论和邻接矩阵的方法，可以大大简化计算过程。
我们构建一个包含6个节点的图，分别代表高度值1至6。如果两个数字可以相邻（即差值不为5），就在对应的节点间添加一条边，并允许每个节点有自环（表示同一高度连续出现）。由此得到反映槽高允许相邻关系的图结构。
基于此图建立邻接矩阵 $ A $：若节点 $ i $ 与 $ j $ 可相邻，则 $ a_{ij} = 1 $，否则为0。例如，1与2可相邻，故 $ a_{12} = a_{21} = 1 $；但1与6不可相邻，因此 $ a_{16} = a_{61} = 0 $。同时，由于允许相同高度连续出现，所有对角线元素均为1。
此时，矩阵 $ A $ 的元素总和表示长度为2、满足相邻约束的槽高组合数。更一般地，$ A^k $ 中所有元素之和表示长度为 $ k+1 $ 的合法序列数量。对于本题中的5个槽，相当于寻找长度为5的路径数，也就是经过4次转移，因此需要计算 $ A^4 $。
计算得 $ A^4 $ 的所有元素之和为6306，这意味着满足“相邻高度差不为5”的5槽锁具共有6306种。
然而题目还要求“至少有3个不同的高度”。因此还需从中剔除仅含1种或2种高度的非法情况：
- 仅含1种高度的组合：共6种（全为1、全为2……全为6）；
- 仅含2种高度的组合：需进一步排除那些虽有两种但违反差值限制或未达到多样性要求的情形，经分析此类有效组合总数为若干（具体依规则推导）。
最终合法锁具总数为：6306 减去仅含1种和2种高度的组合数，得出符合条件的一批锁具总数。再以此总数除以60，即可确定可装箱的数量。
通过这个例子可以看出，原本复杂的组合问题，借助图的建模与邻接矩阵的幂运算，被有效地转化为线性代数中的矩阵操作，实现了化繁为简的目标。
我们通过图论中的邻接矩阵方法，成功计算出一批锁具的数量。具体推导如下： 经过计算可得： \[ 6306 - \left(6 + \left(C_6^2 - 1\right)\left(2^5 - 2\right)\right) = 5880 \] 因此，这批锁具的总数为5880个。若每箱可装60个，则总共需要装 $ 5880 / 60 = 98 $ 箱。 相比其他解法，该方法借助邻接矩阵这一图论工具，使问题的求解过程更加清晰简洁。其中涉及的 $ A^k $ 在图论中的含义，参考了刘亚国在《图论中邻接矩阵的应用》一文中的相关论述。关联矩阵的实际应用
在邻接矩阵的基础上进一步拓展，我们将无向边升级为有向边，从而引入另一种重要的矩阵结构——关联矩阵。这种矩阵常用于描述图中边与顶点之间的连接关系。以下是一个包含4个节点和6条边的有向图示例：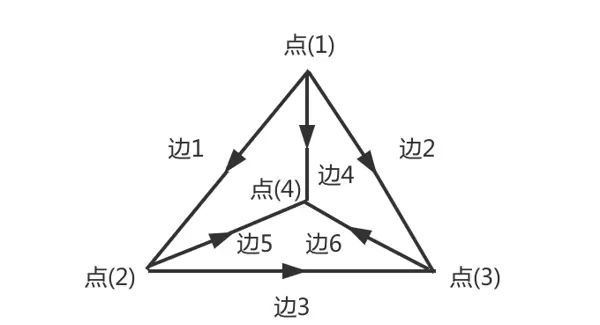
为了描述该图的结构，我们构建一个6×4的矩阵，其中列对应节点（1）至（4），行对应边1至边6：
$$
A =
\begin{bmatrix}
-1 & 1 & 0 & 0 \\
-1 & 0 & 1 & 0 \\
-1 & 0 & 0 & 1 \\
0 & -1 & 1 & 0 \\
0 & -1 & 0 & 1 \\
0 & 0 & -1 & 1 \\
\end{bmatrix}
$$
矩阵中的元素仅由 -1、1 和 0 构成：-1 表示该边从此节点出发（出度），1 表示该边指向此节点（入度），0 则表示该边与此节点无关。例如，第一行为 [-1, 1, 0, 0]，说明边1从节点(1)指向节点(2)，而与节点(3)和(4)无关联。
应用于电路分析
关联矩阵在现实中有广泛应用，尤其在电子电路拓扑结构分析中表现突出。结合基尔霍夫定律，可用于复杂电路的建模与求解。设 $ x_1, x_2, x_3, x_4 $ 分别代表四个节点的电压值，考虑矩阵乘积 $ Ax $ 的结果： $$ Ax = \begin{bmatrix} x_2 - x_1 \\ x_3 - x_1 \\ x_4 - x_1 \\ x_3 - x_2 \\ x_4 - x_2 \\ x_4 - x_3 \\ \end{bmatrix} $$ 可以看出，结果向量表示的是各条边上对应的电势差。只要有电势差存在，就可能产生电流。那么当 $ Ax = 0 $ 时意味着什么？此时所有边上的电势差均为零，即所有节点电压相等。这表明系统处于平衡状态，没有电流流动。 同理，若将电压替换为温度，该模型也可用于热传导系统的分析，判断是否存在热量传递。 进一步地，回顾线性代数中“零空间”的概念（如第八篇所述），它指的是满足 $ Ax = 0 $ 的所有向量 $ x $ 所构成的空间，记作 $ \mathrm{ker}(\phi) $，其维度称为零化度（nullity），表示为 $ \dim(\mathrm{ker}(\phi)) $。 在当前电路例子中，$ Ax = 0 $ 的解集表示所有六个电势差为零的情况，这意味着四个节点的电压相同。因此，每一个满足条件的 $ x $ 都是形如 $ (c, c, c, c) $ 的常向量。由此可见，矩阵 $ A $ 的零空间是一条直线。无论整体电压如何同步升降（改变常数 $ c $），都不会影响电势差为零的状态。关联矩阵与基尔霍夫电流定律
接下来，我们探讨关联矩阵在基尔霍夫电流定律中的应用。考虑一个具有4个节点和5条边的新图结构：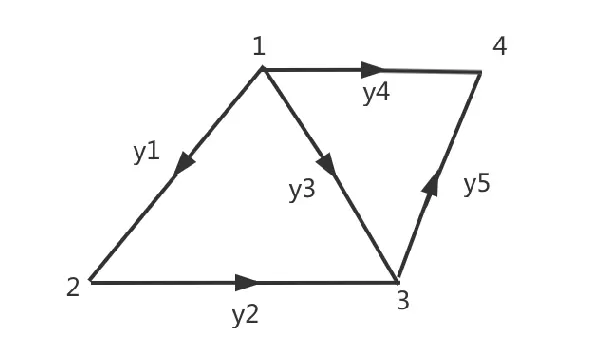
根据基尔霍夫电流定律，流入任一节点的电流总和等于流出的电流总和，数学表达为：
$$ A^T y = 0 $$
其中 $ y = (y_1, y_2, y_3, y_4, y_5)^T $ 是边上的电流向量。
将上述图结构写成关联矩阵形式：
$$
A =
\begin{bmatrix}
-1 & 0 & 0 & -1 & 0 \\
1 & -1 & 0 & 0 & 0 \\
0 & 1 & -1 & 0 & -1 \\
0 & 0 & 1 & 1 & 1 \\
\end{bmatrix}
$$
这里每一行对应一个节点，每一列对应一条边。以第一个节点为例，对应第一行为 $[-1, 0, 0, -1, 0]$，与 $ y $ 相乘后得到：
$$ -y_1 - y_4 = 0 $$
即流入节点(1)的电流之和为零，符合基尔霍夫电流守恒原则。
综上所述，关联矩阵不仅能够刻画图的结构特征，还能有效支持物理系统的建模，广泛应用于电路、网络流、热传导等领域。首先，第一行与向量 y 相乘后结果为：
y - y = 0，这表明从节点1流出的总电流为零，符合基尔霍夫电流定律中的守恒原则；
接着看第二行，与 y 向量相乘后同样得到：
y - y = 0，说明流入节点2的电流与流出该节点的电流大小相等，保持平衡；
随后的第三行与 y 向量进行运算后得出：
y + y - y = 0，反映出在对应节点上电流的流入与流出依然满足守恒关系；
第四行与 y 向量相乘的结果为：
y + y = 0，这一等式也与电路图中所示的电流分布情况完全一致，均遵循电流守恒规律。
至此，关于简单电路背后的数学原理——即关联矩阵的基本概念，已经介绍完毕。当面对更为复杂的电路结构时，例如在某些支路（边）上存在电流源的情况下，原本的齐次方程组 ATy = 0 将不再适用，此时需要将其推广为非齐次形式：ATy = f，其中 f 表示各节点上的外部电流注入情况。
京公网安备 11010802022788号
