结构方程模型(Structural Equation Modeling, SEM)是多元统计分析中的核心方法之一,广泛应用于心理学、管理学及社会科学等领域。该方法不仅能同时处理多个因变量,还可对潜在变量之间的因果关系进行建模与验证,为理论假设的实证检验提供了强有力的工具。本文将围绕SEM的基本原理、分析流程以及在SPSSAU平台上的实际操作展开系统阐述。
1. 结构方程模型的核心构成
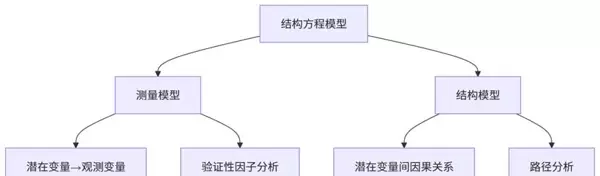
结构方程模型由两个关键部分组成:测量模型和结构模型。其中,测量模型用于刻画潜在变量与其对应的观测指标之间的关系;而结构模型则聚焦于潜在变量之间设定的因果路径。
相较于传统的回归或因子分析方法,SEM具备多项显著优势:
- 可同时分析多个因变量:支持构建复杂的多变量因果网络;
- 允许测量误差的存在:明确纳入观测变量的测量不精确性;
- 整体模型拟合评估:不仅关注单个参数的显著性,还从全局角度判断模型与数据的匹配程度;
- 理论驱动建模能力:提供量化手段来验证预设的理论框架是否成立。
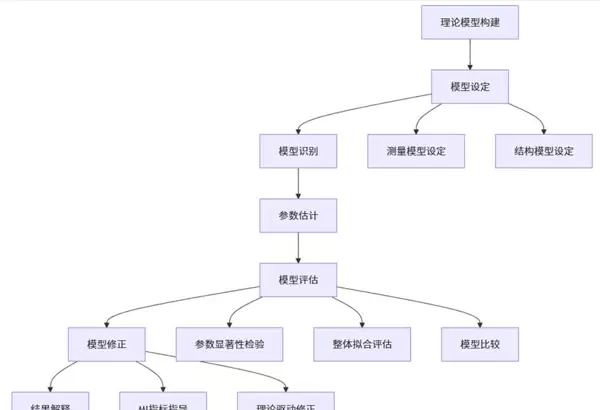
2. SEM分析的标准流程(基于SPSSAU平台)
在SPSSAU中执行结构方程模型遵循一套逻辑清晰且具有迭代特征的步骤:
- 理论模型构建
- 模型设定(包括模型识别、测量模型定义、结构路径设计)
- 参数估计
- 模型评估(涵盖参数显著性、整体拟合优度、模型比较等)
- 模型修正(依据MI建议与理论指导)
- 结果解释与报告输出
这一过程体现了SEM分析的系统性和动态调整特性。SPSSAU通过高度自动化的设计,显著降低了用户在技术实现层面的操作难度。
下图为SPSSAU软件中进行SEM建模的实际操作界面示例:
3. 测量模型与结构模型的双层架构
结构方程模型本质上是一个包含双重子系统的复合体系。
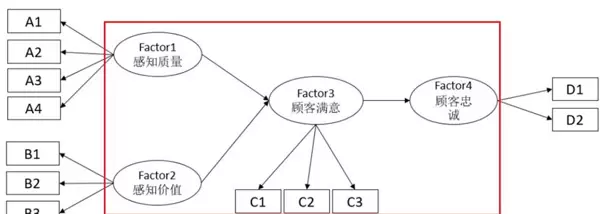
(1)测量模型(Measurement Model)
其作用是利用可观测的问卷题项来反映不可直接测量的潜在构念(潜变量)。例如:
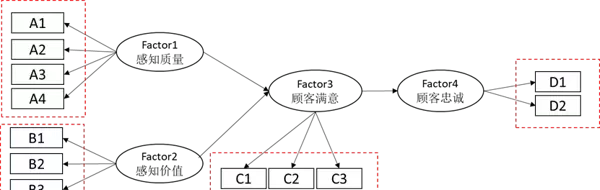
图中每个“Factor → 题项”的箭头表示一条测量路径,对应一个标准化回归系数(即因子载荷),用以衡量该题项对潜变量的代表性强弱。
从理论角度看:
- 高系数值意味着题项能有效代表该潜变量;
- 低系数可能表明题项解释力不足;
- 若未通过显著性检验,则提示存在测量偏差或理论设定需重新审视。
(2)结构模型(Structural Model)
该部分描绘的是潜变量之间的因果关系网络,每条路径(Factor→Factor)代表一项理论假设,说明前因潜变量对后果潜变量的影响方向与强度。这些路径共同构成了整个模型的理论骨架。
4. SPSSAU输出结果的关键指标解读
SPSSAU生成的SEM报告包含多类重要统计量,以下按逻辑顺序划分为五个维度进行解析。
(一)路径系数类指标:揭示影响的方向与强度
| 指标 | 理论意义 | 说明 |
|---|---|---|
| 非标准化系数 | 反映原始尺度下的影响大小 | 用于模型估计,但不便于跨变量比较 |
| 标准化系数(β) | 不同路径间的相对影响强度 | 可用于比较各潜变量间的作用力度 |
| SE(标准误) | 参数估计的稳定性 | 数值越小,估计越可靠 |
| z 值 / CR 值 | 用于检验路径是否显著异于零 | 通常结合p值判断显著性 |
| p 值 | 统计显著性判定依据 | <0.05 表示该路径具有统计意义 |
理想情况下,主要路径应具有统计显著性,标准化系数符号应符合理论预期,且测量项的载荷值较高,以确保潜变量定义的有效性。
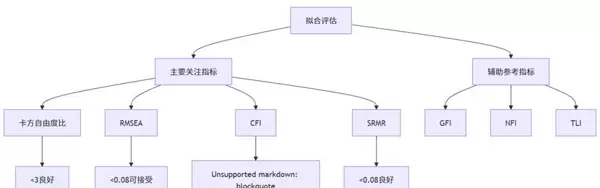
(二)模型拟合指标:评估整体适配程度
模型拟合是SEM区别于其他方法的重要特征。SPSSAU自动计算多种常用拟合指数,并提供解读建议。
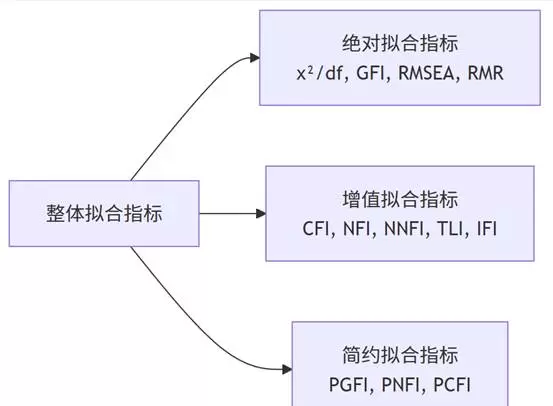
主要拟合指标及其含义如下:
- χ/df:卡方自由度比,越接近1越好,反映模型残差水平;
- GFI(拟合优度指数):表示模型对样本协方差矩阵的还原能力;
- RMSEA(近似误差均方根):衡量模型复杂度与拟合误差的平衡;
- RMR/SRMR:标准化残差均值,数值越小越好;
- CFI/NFI/TLI/IFI:增量拟合指数,体现相对于基准模型的改进程度;
- PGFI/PNFI/PCFI:考虑简约原则的拟合调整指标。
需要注意的是,不可能所有指标都达到最优,因此应强调“整体合理”原则——多数关键指标达标即可接受模型。SPSSAU内置了智能判断机制,在“分析建议”中会自动提示模型质量。
(三)R 决定系数表:衡量解释力分布
SPSSAU会输出每个潜变量和观测变量的 R 值,表示其被前置变量所解释的方差比例。
- 潜变量R:反映结构模型中变量的预测能力;
- 测量项R:体现题项受潜变量影响的程度;
- 若多个R偏低,可能提示模型遗漏重要路径或测量效度存在问题。
(四)MI(Modification Index)修正指数:辅助模型优化
MI值用于识别模型中可能被忽略但具有潜在共变关系的变量组合。SPSSAU自动生成“协方差关系建议表”,用户可选择查看MI结果。
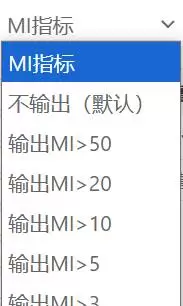
理论提醒:
- 较高的MI值提示两变量间可能存在未设定的关联;
- 但任何修正都必须基于理论合理性,避免仅凭数值机械添加路径;
- SPSSAU在报告中特别指出:“不应完全依赖MI进行模型调整”。
(五)残差项与协方差:检视模型稳健性
除主路径外,SPSSAU还提供残差项估计及相关协方差参数,帮助研究者进一步评估模型的稳定性和误差结构,为深入诊断模型问题提供支持。
残差(Error term)用于表示模型中未能被解释的部分,体现了观测值与预测值之间的差异。通常情况下,残差越小,说明模型对数据的拟合程度越高,整体稳定性也更强。
协方差矩阵则用来刻画外生变量之间的相互关系,揭示它们在模型中的相关结构,是评估模型设定合理性的重要依据之一。
借助SPSSAU平台,结构方程模型(SEM)的分析过程得以极大简化。用户仅需通过“拖拽变量 → 自动拟合 → 一键输出 → 可视化解释”的操作流程,即可完成复杂的建模任务。该工具将原本具有较高专业门槛的统计方法转化为可重复使用的标准化模型,显著降低了学习与应用难度。
更重要的是,SPSSAU能够直接生成模型结果图,帮助研究者在可视化路径图中直观把握变量间的理论关系,使抽象的因果机制变得“看得见,算得清”。如下图所示:
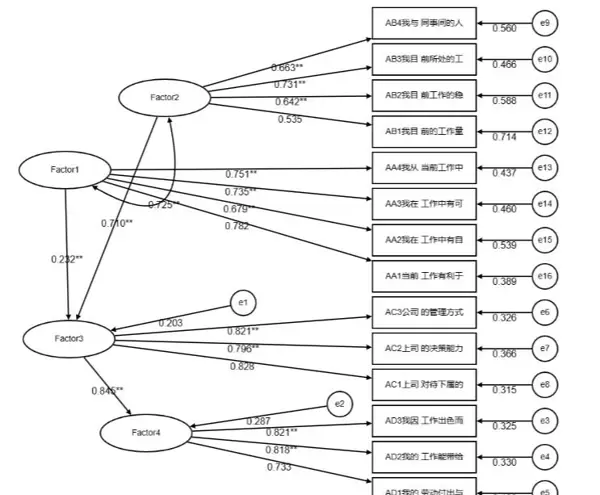
综上所述,结构方程模型不仅能够有效表达潜在的理论架构,还能精确量化测量效度,是一种兼具理论性与实证性的强大分析方法。




 雷达卡
雷达卡







 京公网安备 11010802022788号
京公网安备 11010802022788号







