MATLAB实现:基于二阶锥松弛的主动配电网故障重构与可视化分析
关键词:配电网、故障重构、二阶锥松弛、可视化
参考文献包括《基于禁忌克隆遗传算法的配电网故障恢复重构_张利民》中的故障重构建模方法,以及《二阶锥松弛在配电网最优潮流计算中的应用_陈怀毅》中关于SOCP松弛的技术思路。
仿真环境采用MATLAB平台,结合yalmip工具箱进行模型构建,并调用cplex求解器完成优化计算。整体代码设计围绕一个核心目标展开:建立一种基于二阶锥松弛(SOCP)的主动配电网故障重构模型,有效解决传统非线性潮流方程难以高效求解的问题。
模型核心:二阶锥松弛技术的应用
配电网中的潮流约束本质上是非凸且非线性的,直接求解存在收敛困难和计算效率低下的问题。为此,本方案引入二阶锥松弛方法,将原始的非线性潮流方程转化为可高效处理的二次约束形式。
关键转化步骤体现在以下代码段中:
% 支路潮流约束
for k=1:nbranch
i = branch(k,1); j = branch(k,2);
Pij = sdpvar(1); Qij = sdpvar(1);
constraints = [constraints,
P(k) == Pij - r(k)*(I(k)^2),
Q(k) == Qij - x(k)*(I(k)^2),
u(j) == u(i) - 2*(r(k)*Pij + x(k)*Qij) + (r(k)^2 + x(k)^2)*I(k)^2,
norm([2*Pij; 2*Qij; u(i)-I(k)^2)],2) <= u(i)+I(k)^2]; % SOC约束
end通过使用norm函数对电压与功率关系进行数学重构,原本复杂的非凸表达被转换为满足二阶锥条件的等价形式。特别值得注意的是末尾添加的SOC约束项,它在保证模型可行性的同时,显著提升了松弛精度,是整个建模过程的关键所在。
故障设置与拓扑优化机制
系统支持自定义任意线路作为故障对象,只需调整相应的线路状态矩阵即可触发重构流程。例如,在指定支路发生跳闸时,可通过修改开关状态参数快速模拟实际运行场景:
fault_branch = 15; % 指定故障线路
branch_status(fault_branch) = 0; % 断开故障线路随后启动改进型禁忌克隆遗传算法进行最优网络结构搜索。该算法融合了禁忌搜索的记忆特性与克隆选择的全局探索能力,能够在复杂可行域中高效寻优。
其种群进化策略的设计尤为关键:
while gen < max_gen
% 克隆扩增
clones = repmat(pop(top_indices,:), clone_num, 1);
% 自适应变异
mutation_strength = 0.1*(1 - gen/max_gen);
clones = clones + mutation_strength.*randn(size(clones));
% 禁忌筛选
feasible_clones = check_radial(clones);
% 精英保留
new_pop = [pop(top_indices,:); feasible_clones];
end该机制模拟生物进化过程,在解空间中不断探索新的拓扑组合。其中,禁忌列表避免重复访问已评估结构,提升搜索效率;而自适应变异操作则根据迭代进度动态调节扰动强度,实现局部开发与全局探索之间的良好平衡。
可视化展示:电网状态的直观呈现
为了增强结果可读性与决策支持能力,系统集成了图形化展示模块,能够实时反映网络拓扑变化与运行状态分布。
借助颜色编码与线条样式区分不同元件状态,可视化界面呈现出清晰的空间逻辑关系:
function plot_grid(status)
hold on;
% 绘制正常线路
plot_normal_lines(branch(status==1,:));
% 高亮故障线路
plot(branch(fault_branch,1:2), 'r--', 'LineWidth',3);
% 标记重构线路
scatter(new_nodes(:,1), new_nodes(:,2), 100, 'g', 'filled');
% 拓扑校验
if check_radial(status)
title('辐射状拓扑校验通过');
end
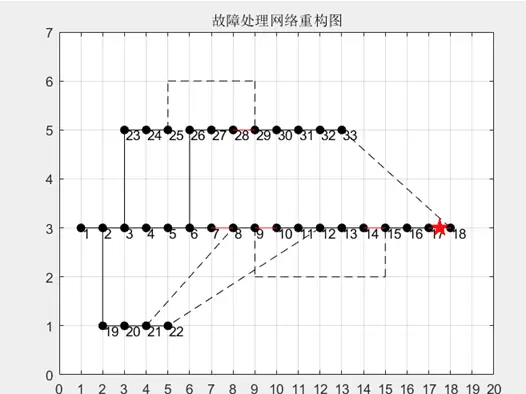
end图中红色虚线代表发生故障并断开的线路,绿色节点标识新投入运行的联络开关位置,其余正常运行部分以实线连接显示。这种“上帝视角”式的展示方式,使运维人员能迅速掌握供电恢复路径与孤岛划分情况,极大提升了应急响应效率。
工程实用性与扩展潜力
该代码不仅具备严谨的数学基础,更注重实际应用场景的适配性。例如,当负荷出现突变或分布式电源出力波动时,仅需更新对应节点的注入功率参数,系统即可自动重新计算最优运行方式。
以往需要数小时人工校验是否满足辐射状结构的工作,如今通过调用check_radial()函数便可实现秒级判断,大幅缩短了决策周期。
总体而言,该方案将高深的数学优化理论转化为稳定可靠的工程实现工具,体现了理论研究与实践需求的高度融合。对于从事配电网自动化、智能调度或故障恢复研究的技术人员来说,这是一套极具参考价值的完整实现范例。
面对电网突发故障,这套方法提供了一种高效、精准的应对思路——无需慌乱,让二阶锥来搞定。




 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







