[图行天下] COMSOL在铌酸锂波导物理模型中的光学模式分析：群速度色散与有效模式面积的探究 [推广有奖]

0关注
0粉丝

等待验证会员

学前班

40%

还不是VIP/贵宾

威望: 0 级
论坛币: 0 个
通用积分: 0.0417
学术水平: 0 点
热心指数: 0 点
信用等级: 0 点
经验: 20 点
帖子: 1
精华: 0
在线时间: 0 小时
注册时间: 2018-11-15
最后登录: 2018-11-15

楼主

海水梦悠悠 发表于 2025-12-12 11:22:42 |AI写论文

是否 +2 论坛币

k人参与回答

经管之家送您一份

应届毕业生专属福利!

求职就业群

赵安豆老师微信：zhaoandou666

经管之家联合CDA

送您一个全额奖学金名额~ !

立即领取

感谢您参与论坛问题回答

经管之家送您两个论坛币！

+2 论坛币

COMSOL光学模式分析：铌酸锂波导群速度色散与有效模式面积物理模型

近年来，铌酸锂波导在光子芯片领域迅速走红，成为研究热点。这种材料究竟有何独特之处？对于从事集成光学器件开发的研究者而言，理解其群速度色散特性至关重要——它直接影响光脉冲的展宽行为；而有效模式面积则决定了光场与材料之间的相互作用强度，即“光-物质”耦合的紧密程度。本文将借助COMSOL Multiphysics平台，深入剖析这两项关键参数背后的物理机制。

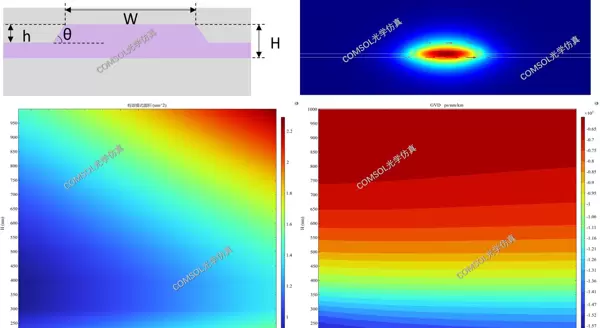
首先构建基本几何结构是仿真的起点。以下模型采用典型的波导尺寸：横截面宽度为2.5μm，厚度为0.5μm。

model = ModelUtil.create('LiNbO3_Waveguide');
model.geom.create('geom1', 3);
model.geom('geom1').create('wp1', 'WorkPlane');
model.geom('geom1').feature('wp1').set('planetype', 'xy');
model.geom('geom1').feature('wp1').create('r1', 'Rectangle');
model.geom('geom1').feature('wp1').feature('r1').set('size', {'2.5[um]' '0.5[um]'});

代码中使用[um]作为单位标注，COMSOL会自动将其转换为国际单位制中的米，从而避免因手动换算导致的数值错误，提升建模效率和准确性。

材料属性的设定是整个仿真过程的核心环节。铌酸锂作为一种各向异性晶体，其介电张量需精确描述：

model.material.create('mat1', 'Commonly_Used_Materials', 'lithium_niobate');
model.material('mat1').propertyGroup('def').set('epsilonr', {'nx^2' '0' '0'; '0' 'ny^2' '0'; '0' '0' 'nz^2'});
model.material('mat1').propertyGroup('def').set('electricconductivity', 0);

其中折射率分量分别为 nx = 2.14、ny = 2.14、nz = 2.21，体现出明显的双折射特性。这种各向异性将导致TE模与TM模在传播过程中表现出不同的色散行为，进而影响偏振相关器件的设计。

在边界条件设置方面，存在一个常见误区需要特别注意：

model.physics.create('emw', 'ElectromagneticWaves', 'geom1');
model.physics('emw').create('pc1', 'PerfectConductor', 2);
model.physics('emw').feature('pc1').selection.set([3 4]);

虽然将上下表面设为完美电导体（PEC）看似简化计算，但可能引入非物理的寄生模式，干扰真实模式的提取。推荐使用散射边界条件（SBC）或完美匹配层（PML），尤其是在分析泄漏模或宽带响应时更为可靠。需要注意的是，采用此类吸收边界时，仿真区域应足够大以减少反射干扰。

接下来是有效模式面积的计算，该参数反映了光场在波导中的局域化程度：

E_field = mphgetexpressions(model, 'emw.E');
int_exp = real(dot(E_field, E_field));
A_eff = (integrate(int_exp))^2 / integrate(int_exp^2);

公式中分子部分为电场幅值平均值的平方，分母为电场幅值平方的平均值。当光场越集中于波导核心区域时，所得A_eff越小，意味着更强的非线性效应。这一特性正是铌酸锂微环谐振器能够实现高效二阶非线性频率转换（如倍频）的重要原因。

至于群速度色散（GVD）的提取，则依赖于对传播常数β的数值微分处理：

lambda = linspace(1.5,1.6,20)*1e-6; % 扫描1500-1600nm
beta = zeros(size(lambda));
for i = 1:length(lambda)
    model.param.set('lambda0', lambda(i));
    model.study('std1').run;
    beta(i) = real(model.solution('sol1').getNodalData('beta'));
end
D = - (lambda.^2/(2*pi*3e8)) .* gradient(gradient(beta,lambda),lambda);

具体流程为：在一定波长范围内进行参数扫描，获取对应的β值序列；随后通过二次数值微分计算得到色散参数D。注意公式中的负号不可忽略，它决定了色散类型的正负——正值对应正常色散，负值则为反常色散。实验模拟发现，当波导横向尺寸减小至1μm以下时，色散曲线可能出现异常震荡，这通常源于高阶导模的参与或模式耦合效应。

最后提出一个关键问题：为何相比硅基波导，铌酸锂体系更易于实现色散调控？答案隐藏在其优异的电光性能之中——铌酸锂具有显著的Pockels效应，外加电场可动态调节局部折射率分布，相当于为色散曲线配备了实时可调的“方向盘”。这项能力使其在可重构光子电路中具备巨大潜力，相关内容值得后续专题探讨。