作为机器学习初学阶段的重要算法之一,朴素贝叶斯分类器凭借其清晰的理论基础和高效的运算能力,广泛应用于各类分类任务中。本实验以经典的西瓜数据集为基础,构建并实现一个朴素贝叶斯分类模型,完成对“好瓜”与“坏瓜”的预测任务,从而深入掌握贝叶斯定理及特征条件独立假设的实际应用。
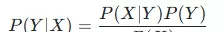 为了进行分类决策,采用后验概率最大化原则:
为了进行分类决策,采用后验概率最大化原则:
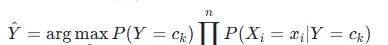 针对离散特征可能出现的概率为零问题,引入拉普拉斯平滑处理:
针对离散特征可能出现的概率为零问题,引入拉普拉斯平滑处理:
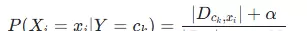 对于连续型特征(如密度、含糖率),使用高斯分布建模其概率密度函数:
对于连续型特征(如密度、含糖率),使用高斯分布建模其概率密度函数:


一、实验原理说明
1. 基本思想
该分类器的核心依据是贝叶斯定理,通过计算每个类别的后验概率,并选择概率最大的类别作为最终预测结果。所谓“朴素”,即假设所有特征之间相互独立,这一简化显著降低了联合概率的计算难度,使得模型在有限样本下仍能高效运行。2. 关键公式表达
贝叶斯定理用于计算后验概率: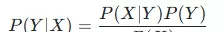 为了进行分类决策,采用后验概率最大化原则:
为了进行分类决策,采用后验概率最大化原则:
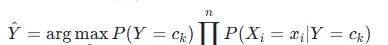 针对离散特征可能出现的概率为零问题,引入拉普拉斯平滑处理:
针对离散特征可能出现的概率为零问题,引入拉普拉斯平滑处理:
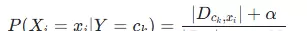 对于连续型特征(如密度、含糖率),使用高斯分布建模其概率密度函数:
对于连续型特征(如密度、含糖率),使用高斯分布建模其概率密度函数:

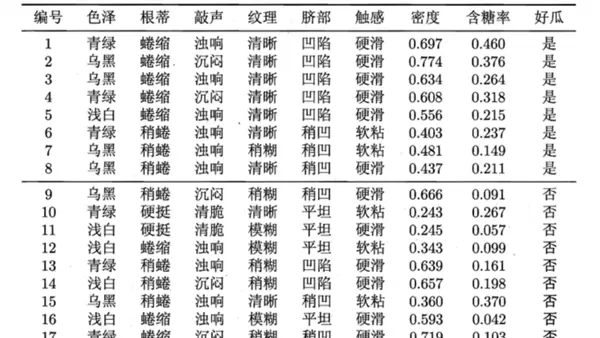
3. 数据集描述
实验所用西瓜数据集共包含17个训练样本,每个样本具有8个属性特征:其中6个为离散变量——色泽、根蒂、敲声、纹理、脐部、触感;2个为连续变量——密度和含糖率。分类标签为“好瓜”或“坏瓜”。测试样本选取自训练集中第一个标记为“好瓜”的实例,用以验证模型的准确性。二、代码实现过程
1. 数据预处理
首先整理原始训练数据与测试样本,明确各特征的数据类型及其取值范围,同时标注目标类别:

import numpy as np?
from collections import defaultdict?
("浅白", "蜷缩", "浊响", "清晰", "凹陷", "硬滑", 0.556, 0.215, "是"),?
("青绿", "稍蜷", "浊响", "清晰", "稍凹", "软粘", 0.403, 0.237, "是"),?
("乌黑", "稍蜷", "浊响", "稍糊", "稍凹", "软粘", 0.481, 0.149, "是"),?
("乌黑", "稍蜷", "浊响", "清晰", "稍凹", "硬滑", 0.437, 0.211, "是"),?
# 坏瓜(否)?
("乌黑", "稍蜷", "沉闷", "稍糊", "稍凹", "硬滑", 0.666, 0.091, "否"),?
("青绿", "硬挺", "清脆", "清晰", "平坦", "软粘", 0.243, 0.267, "否"),?
("浅白", "硬挺", "清脆", "模糊", "平坦", "硬滑", 0.245, 0.057, "否"),?
("浅白", "蜷缩", "浊响", "模糊", "平坦", "软粘", 0.343, 0.099, "否"),?
("青绿", "稍蜷", "浊响", "稍糊", "凹陷", "硬滑", 0.639, 0.161, "否"),?
("浅白", "稍蜷", "沉闷", "稍糊", "凹陷", "硬滑", 0.657, 0.198, "否"),?
("乌黑", "稍蜷", "浊响", "清晰", "稍凹", "软粘", 0.360, 0.370, "否"),?
("浅白", "蜷缩", "浊响", "模糊", "平坦", "硬滑", 0.593, 0.042, "否"),?
("青绿", "蜷缩", "沉闷", "稍糊", "稍凹", "硬滑", 0.719, 0.103, "否"),?
]?
?
# 测试样本?
test_sample = ("青绿", "蜷缩", "浊响", "清晰", "凹陷", "硬滑", 0.697, 0.460)2. 分类器结构设计
采用面向对象编程方式封装朴素贝叶斯分类器,包含训练模块、概率估计模块以及预测功能模块:class NaiveBayesClassifier:
def __init__(self, alpha=1):
self.alpha = alpha # 拉普拉斯平滑系数
self.class_count = defaultdict(int) # 类别计数
self.discrete_feat_stats = defaultdict(lambda: defaultdict(lambda: defaultdict(int))) # 离散特征统计
self.continuous_feat_stats = defaultdict(lambda: defaultdict(dict)) # 连续特征统计(均值、方差)
self.discrete_feat_names = ["色泽", "根蒂", "敲声", "纹理", "脐部", "触感"]
self.continuous_feat_names = ["密度", "含糖率"]
self.total_samples = 0
def fit(self, data):
"""训练模型,统计各类别和特征的概率分布"""
self.total_samples = len(data)
for sample in data:
label = sample[-1]
self.class_count[label] += 1
# 统计离散特征(前6个)
for i in range(6):
feat_val = sample[i]
self.discrete_feat_stats[label][self.discrete_feat_names[i]][feat_val] += 1
# 收集并计算连续特征的均值和方差
density_data = [s[6] for s in data if s[-1] == label]
sugar_data = [s[7] for s in data if s[-1] == label]
self.continuous_feat_stats[label]["密度"] = {
"mean": np.mean(density_data),
"var": np.var(density_data) if np.var(density_data) != 0 else 1e-6
}
self.continuous_feat_stats[label]["含糖率"] = {
"mean": np.mean(sugar_data),
"var": np.var(sugar_data) if np.var(sugar_data) != 0 else 1e-6
}
def _laplace_smooth(self, label, feat_name, feat_val):
"""拉普拉斯平滑计算离散特征的条件概率 P(feat=val | label)"""
count = self.discrete_feat_stats[label][feat_name].get(feat_val, 0)
class_total = self.class_count[label]
feat_vals = set([s[self.discrete_feat_names.index(feat_name)] for s in train_data])
feat_size = len(feat_vals)
return (count + self.alpha) / (class_total + self.alpha * feat_size)
def _gaussian_prob(self, label, feat_name, feat_val):
"""高斯分布计算连续特征的条件概率 P(feat=val | label)"""
stats = self.continuous_feat_stats[label][feat_name]
mean, var = stats["mean"], stats["var"]
exponent = np.exp(-(feat_val - mean) ** 2 / (2 * var))
return (1 / np.sqrt(2 * np.pi * var)) * exponent
def predict(self, sample):
"""预测样本类别,返回结果和概率详情"""
posteriors = {}
prob_details = {} # 存储各特征的条件概率详情
for label in self.class_count.keys():
# 先验概率 P(label)
prior = self.class_count[label] / self.total_samples
prob_details[label] = {"先验概率": prior}
current_prob = prior
# 离散特征条件概率(累乘)
for i in range(6):
feat_name = self.discrete_feat_names[i]
feat_val = sample[i]
cond_prob = self._laplace_smooth(label, feat_name, feat_val)
prob_details[label][f"{feat_name}={feat_val}"] = cond_prob
current_prob *= cond_prob
# 连续特征条件概率(累乘)
for i, feat_name in enumerate(self.continuous_feat_names):
feat_val = sample[6 + i]
cond_prob = self._gaussian_prob(label, feat_name, feat_val)
prob_details[label][f"{feat_name}={feat_val}"] = cond_prob
current_prob *= cond_prob
posteriors[label] = current_prob
# 取后验概率最大的类别
pred_label = max(posteriors, key=posteriors.get)
return pred_label, posteriors, prob_details3. 模型训练与分类预测
执行训练流程,统计先验概率与各类别下的特征条件概率,并基于测试样本输入完成分类推理:if __name__ == "__main__":
# 初始化并训练模型
nb = NaiveBayesClassifier(alpha=1)
nb.fit(train_data)
# 预测测试样本
pred_label, posteriors, prob_details = nb.predict(test_sample)
# 格式化输出结果
print("=" * 60)
print("朴素贝叶斯分类预测结果(西瓜数据集)")
print("=" * 60)
# 输出各类别概率详情
for label in ["是", "否"]:
print(f"\n【{label}(好瓜={label})】")
for feat, prob in prob_details[label].items():
if "先验概率" in feat:
print(f" {feat}: {prob:.6f}")
else:
print(f" P({feat}|好瓜={label}): {prob:.6f}")
post_prob = posteriors[label]
print(f" 后验联合概率: {post_prob:.10f}")
print("\n" + "=" * 60)
print(f"最终分类结果:该样本是【{pred_label}】好瓜")
print("=" * 60)三、实验结果分析
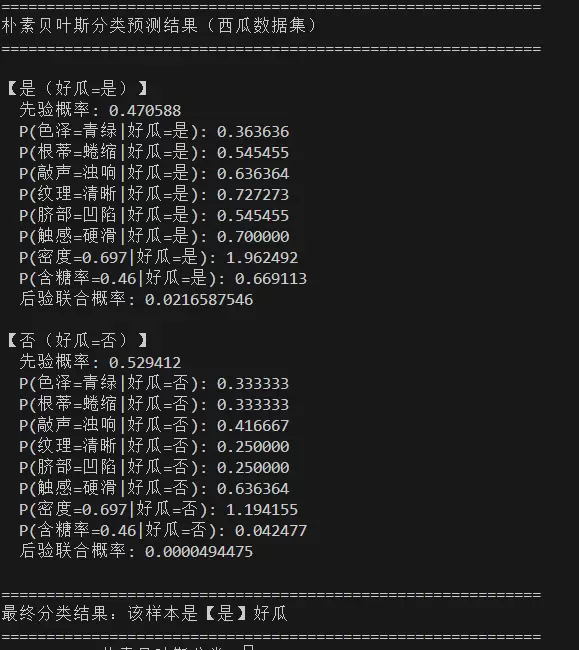
1. 输出展示
模型输出如下所示:




 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







