机器学习——贝叶斯分类

是 否 +2 论坛币

k人 参与回答

经管之家送您一份

应届毕业生专属福利!

求职就业群

赵安豆老师微信：zhaoandou666

经管之家联合CDA

送您一个全额奖学金名额~ !

立即领取

感谢您参与论坛问题回答

经管之家送您两个论坛币！

+2 论坛币

一、理论根基：深入理解贝叶斯定理

贝叶斯分类的全部逻辑都建立在贝叶斯定理之上。该定理的核心思想是——“利用新出现的信息，动态调整对某一事件发生概率的判断”，而不是凭空推测结果。为了更好地理解这一定理，我们先明确三个关键的概率概念，并结合生活中的例子进行说明：

• 先验概率 P(A)：在没有任何额外信息的情况下，事件A发生的初始概率。例如，“随机抽取一名成年人，其患有糖尿病”的概率，仅依据整体人群的患病比例得出，不涉及任何个体体检数据。
• 似然概率 P(B|A)：在已知事件A已经发生的前提下，观察到事件B出现的概率。例如，“已知某人患有糖尿病（A），其空腹血糖超标（B）”的概率。
• 后验概率 P(A|B)：在观测到事件B之后，反推事件A发生的更新后概率。这是我们真正关心的结果，比如“已知某人空腹血糖超标（B），判断其是否患有糖尿病（A）”的概率。本质上，这是用“血糖超标”这一新证据来修正原有的疾病判断。

贝叶斯定理通过如下数学公式清晰表达了三者之间的关系：

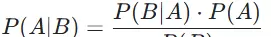
其中，P(B) 是边际概率，表示事件B在所有可能情况下发生的总概率。它的作用是对计算结果进行归一化处理，确保后验概率值落在0到1之间。在实际分类任务中，由于P(B)对于所有类别都是相同的常数，在比较不同类别的后验概率大小时，可以忽略此项，只需关注分子部分即可完成分类决策。

二、模型实现：剖析朴素贝叶斯分类器

将贝叶斯理论应用于实际分类问题的关键工具是“朴素贝叶斯分类器”（Naive Bayes Classifier）。这里的“朴素”并非贬义，而是源于一个核心假设——在给定类别标签的前提下，所有特征彼此独立。正是这个简化假设，使得复杂的概率计算变得可行，推动了贝叶斯方法从理论走向广泛应用。

2.1 条件独立性假设的意义

在现实分类任务中，样本通常包含多个特征（如使用“年龄、血压、血糖”等指标判断是否患病）。若不引入任何假设，直接计算联合概率 P(特征1, 特征2, ..., 特征n | 类别)，会面临严重的“维度灾难”：随着特征数量增加，所需计算量呈指数级上升，导致模型难以训练和部署。

条件独立性假设则提出：在已知类别的情况下，各个特征之间互不影响。例如，“已知某人患病”，那么他的“年龄”与“血压”之间没有关联。尽管这一假设在现实中往往并不完全成立，但它能将高维联合概率分解为各特征条件概率的乘积形式，极大降低计算复杂度。实践证明，即使存在一定程度的特征相关性，该模型在多数场景下仍具备良好的分类性能。

2.2 分类逻辑推导（简化公式版）

分类的目标是：给定一个样本的特征向量 X = (x, x, ..., x)，判断它最可能属于哪一个类别 C（类别集合为 {C, C, ..., C}）。结合贝叶斯定理与条件独立性假设，可得朴素贝叶斯的核心判别规则如下：

最终选择使该表达式最大的类别作为预测输出。

三、实战流程：朴素贝叶斯在西瓜数据集上的应用

“西瓜数据集”是机器学习入门阶段的经典教学案例，广泛用于演示基本分类算法的工作流程。该数据集通过多个特征描述西瓜的外观与内在品质，目标是判断其是否为“好瓜”。以下是基于此数据集的完整实现步骤：

1. 数据准备

首先通过 load_data 函数加载原始数据，并将其划分为特征矩阵和标签向量两部分。西瓜数据集中前6个特征为离散型变量（如色泽、根蒂、敲声等），后两个为连续型变量（密度、含糖率）。

2. 先验概率计算

先验概率 P(Y) 表示每个类别在训练集中出现的基础频率，即在无其他信息条件下某类样本出现的可能性。该步骤由 calc_prior 函数实现：

def calc_prior(labels):
? ? total = len(labels)
? ? priors = defaultdict(float)
? ? for label in labels:
? ? ? ? priors[label] += 1
? ? for k in priors:
? ? ? ? priors[k] /= total
? ? print("先验概率:", dict(priors))
? ? return priors

3. 条件概率估计

针对不同类型特征采用不同的概率估计策略：

• 离散特征：计算 P(Xi|Y)，即在给定类别Y下，某个特征取特定值的概率。实现过程如下：

calc_discrete_probs实现：

def calc_discrete_probs(separated, idx):
? ? probs = {}
? ? for label, items in separated.items():
? ? ? ? freq = defaultdict(int)
? ? ? ? for item in items:
? ? ? ? ? ? freq[item[idx]] += 1
? ? ? ? total = len(items)
? ? ? ? probs[label] = {k: (v / total) for k, v in freq.items()}
? ? return probs

• 连续特征：通常假设其服从高斯分布，通过计算每类样本中该特征的均值与方差来进行建模。对应代码如下：

calc_continuous_probs实现：

def calc_continuous_probs(separated, idx):
? ? stats = {}
? ? for label, items in separated.items():
? ? ? ? values = [item[idx] for item in items]
? ? ? ? mean = sum(values) / len(values)
? ? ? ? var = sum((x - mean) ** 2 for x in values) / len(values)
? ? ? ? stats[label] = (mean, var)
? ? return stats

4. 高斯概率密度函数的应用

对于连续型特征，使用高斯概率密度函数来估算其在某一类别下的出现概率：

def gaussian_prob(x, mean, var):
? ? if var == 0: var = 1e-6 ?# 防止除零
? ? exponent = math.exp(-((x - mean) ** 2) / (2 * var))
? ? return (1 / math.sqrt(2 * math.pi * var)) * exponent

5. 分类预测执行

综合以上各项概率，运用贝叶斯定理计算各类别的后验概率，并选取概率最高的类别作为最终预测结果：

results = {}
for label in priors:
? ? prob = math.log(priors[label]) ?# 使用对数防止下溢
? ? # 乘以各个属性的条件概率
? ? for idx in discrete_idxs:
? ? ? ? val = test_sample[idx]
? ? ? ? prob_dict = discrete_probs[idx].get(label, {})
? ? ? ? p = prob_dict.get(val, 1e-6) ?# 使用小概率值防止零概率
? ? ? ? prob += math.log(p)
? ? for idx in continuous_idxs:
? ? ? ? val = test_sample[idx]
? ? ? ? mean, var = continuous_probs[idx][label]
? ? ? ? p = gaussian_prob(val, mean, var)
? ? ? ? prob += math.log(p)
? ? results[label] = prob

6. 完整代码展示

整合上述所有模块后的完整实现代码如下：

import math
from collections import defaultdict
?
?
def load_data(file_path):
? ? train_data = []
? ? labels = []
? ? with open(file_path, 'r', encoding='utf-8') as f:
? ? ? ? for line in f:
? ? ? ? ? ? parts = line.strip().split()
? ? ? ? ? ? features = parts[:6] + [float(x) for x in parts[6:8]]
? ? ? ? ? ? label = parts[8]
? ? ? ? ? ? train_data.append(features)
? ? ? ? ? ? labels.append(label)
? ? return train_data, labels
?
?
def calc_prior(labels):
? ? total = len(labels)
? ? priors = defaultdict(float)
? ? for label in labels:
? ? ? ? priors[label] += 1
? ? for k in priors:
? ? ? ? priors[k] /= total
? ? print("先验概率:", dict(priors))
? ? return priors
?
?
def separate_by_class(data, labels):
? ? separated = defaultdict(list)
? ? for i in range(len(data)):
? ? ? ? separated[labels[i]].append(data[i])
? ? return separated
?
?
def calc_discrete_probs(separated, idx):
? ? probs = {}
? ? for label, items in separated.items():
? ? ? ? freq = defaultdict(int)
? ? ? ? for item in items:
? ? ? ? ? ? freq[item[idx]] += 1
? ? ? ? total = len(items)
? ? ? ? probs[label] = {k: (v / total) for k, v in freq.items()}
? ? return probs
?
?
def calc_continuous_probs(separated, idx):
? ? stats = {}
? ? for label, items in separated.items():
? ? ? ? values = [item[idx] for item in items]
? ? ? ? mean = sum(values) / len(values)
? ? ? ? var = sum((x - mean) ** 2 for x in values) / len(values)
? ? ? ? stats[label] = (mean, var)
? ? return stats
?
?
def gaussian_prob(x, mean, var):
? ? if var == 0: var = 1e-6 ?
? ? exponent = math.exp(-((x - mean) ** 2) / (2 * var))
? ? return (1 / math.sqrt(2 * math.pi * var)) * exponent
?
?
def classify_naive_bayes(train_data, labels, test_sample):
? ? priors = calc_prior(labels)
? ? separated = separate_by_class(train_data, labels)
?
? ? discrete_idxs = list(range(6))
? ? continuous_idxs = [6, 7]
?
? ? discrete_probs = {}
? ? for idx in discrete_idxs:
? ? ? ? discrete_probs[idx] = calc_discrete_probs(separated, idx)
?
? ? continuous_probs = {}
? ? for idx in continuous_idxs:
? ? ? ? continuous_probs[idx] = calc_continuous_probs(separated, idx)
?
? ? results = {}
? ? for label in priors:
? ? ? ? prob = math.log(priors[label]) ?
? ? ? ? for idx in discrete_idxs:
? ? ? ? ? ? val = test_sample[idx]
? ? ? ? ? ? prob_dict = discrete_probs[idx].get(label, {})
? ? ? ? ? ? p = prob_dict.get(val, 1e-6)?
? ? ? ? ? ? prob += math.log(p)
? ? ? ? for idx in continuous_idxs:
? ? ? ? ? ? val = test_sample[idx]
? ? ? ? ? ? mean, var = continuous_probs[idx][label]
? ? ? ? ? ? p = gaussian_prob(val, mean, var)
? ? ? ? ? ? prob += math.log(p)
? ? ? ? results[label] = prob
?
? ? print("对数后验概率:", results)
?
? ? pred_label = max(results, key=results.get)
? ? print(f"\n预测结果: '{pred_label}' 的概率最大，该瓜为{'好瓜' if pred_label == '是' else '坏瓜'}")
?
?
if __name__ == "__main__":
? ? file_path = "E:/pythonProject/train.txt"
? ? train_data, labels = load_data(file_path)
? ? test_sample = ['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', 0.697, 0.460]
? ? classify_naive_bayes(train_data, labels, test_sample)

7. 实验结果输出

模型运行完成后得到的分类结果如下所示：

四、综合分析：优势、局限与典型应用场景

每种算法都有其适用范围，朴素贝叶斯也不例外。全面认识其优缺点，有助于在实际项目中做出合理的技术选型。

4.1 主要优势

• 计算效率极高：无需迭代优化过程，仅依赖统计计数即可完成模型构建，特别适合处理大规模数据集（如千万级文本分类任务）；
• 实现简单直观：核心逻辑仅涉及基础概率运算，代码简洁，开发门槛低，易于维护和调试；
• 适用于小样本场景：即使训练数据较少，也能通过合理的概率估计获得稳定的分类效果，不易发生过拟合；
• 鲁棒性强：对缺失值和异常点具有较强容忍能力，少量噪声不会显著影响整体分类性能。

4.2 存在的局限性

• 条件独立性假设过强：现实中许多特征存在相关性（如“身高”与“体重”），违背该假设会导致模型估计偏差，影响准确率；
• 对特征分布敏感：若实际特征分布偏离模型预设（如假设为高斯分布但实际非正态），分类效果会明显下降；
• 难以应对高维复杂结构：当特征维度极高（如百万级别）或存在严重多重共线性时，模型性能会显著退化。

4.3 典型适用领域

结合其特性，朴素贝叶斯在以下场景中表现尤为突出：

• 文本分类：包括垃圾邮件识别、新闻主题分类、情感倾向分析、恶意评论过滤等——这也是该算法最为经典且广泛应用的领域。

在小规模数据集的分类任务中，当面临数据量有限、特征维度较低且对模型推理速度有较高要求时，朴素贝叶斯算法常被视为最优方案之一。该方法基于概率统计原理，能够在资源受限的情况下快速完成分类预测，适用于对实时性要求较高的场景。

在医疗领域的辅助诊断应用中，朴素贝叶斯可用于初步判断疾病类型。通过输入患者的生理指标数据，如体温、血压及血常规结果等，模型可依据已有医学数据进行概率推断，辅助医生进行早期筛查与判断。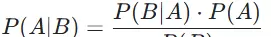

此外，在构建轻量级推荐系统时，若推荐逻辑相对简单、用户行为数据不复杂，该算法也表现出良好的适应性。通过融合用户的基础属性（如年龄、性别）和行为轨迹（如点击记录、收藏偏好），系统能够实现基础个性化推荐，满足低复杂度场景下的推荐需求。

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

分享0 收藏0 回帖

关键词：贝叶斯分类 机器学习 贝叶斯 collections Continuous