机器学习之分类算法之朴素贝叶斯分类——CDA网校

是 否 +2 论坛币

k人 参与回答

经管之家送您一份

应届毕业生专属福利!

求职就业群

赵安豆老师微信：zhaoandou666

经管之家联合CDA

送您一个全额奖学金名额~ !

立即领取

感谢您参与论坛问题回答

经管之家送您两个论坛币！

+2 论坛币

CDA网校致力于以优质的人工智能在线教育资源助力学员的DT职业梦想！课程内容涵盖数据分析、机器学习、深度学习、人工智能、tensorFlow、PyTorch、知识图谱等众多核心技术及行业案例，让每一个学员都可以在线灵活学习，快速掌握AI时代的前沿技术。PS：私信我即可获取CDA会员1个月免费试听机会

最近自己对机器学习比较感兴趣，做个笔记，还请大牛不喜轻喷，多多指教。
朴素贝叶斯分类基于概率论中的贝叶斯原理：
P(A|B) = P(B|A)*P(A)/P(B)
所谓朴素即是特征属性之间相互独立的对分类结果发生影响。
所以对应的概率公式可改写为P(c|x) = P(x|c)|p(c) / P(x)
其中:
    P(c) 是类‘先验概率’
    P(x|c) 是样本x对于类标记c的类条件概率（或称似然）
    P(x)叫做证据因子
由于朴素贝叶斯假定所有特征属性独立，所以
    P(x|c)= P(x1,x2,…xn|c) = P(x1|c)P(x2|c) …P(xn|c)
    P(x) = P(x1) * P(x2) * … * P(xn)
所以
    P(c|x) = P(x1,x2,…xn|c) = P(x1|c)P(x2|c) …P(xn|c) * P(c) /
    p(x)。 因为 P(c) / p(x)是固定值，所以我们一般只需要计算P(x|c)，找出最大似然即可
Ps:
    对于离散属性而言，P(x1|c) = 训练集中属性为x1且分类为c的数目|训练集中分类c的数目
   

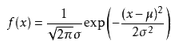
对于离散属性而言，一般假定其概率分布为高斯分布
取个例1：
    症状　　职业　　　疾病
　　打喷嚏　护士　　　感冒
　　打喷嚏　农夫　　　过敏
　　头痛　　建筑工人　脑震荡
　　头痛　　建筑工人　感冒
　　打喷嚏　教师　　　感冒
　　头痛　　教师　　　脑震荡
现在又来了是一个打喷嚏的建筑工人。请问他患上感冒的概率有多大？
由上可知
求P(感冒|打喷嚏建筑工人) = P(建筑工人|感冒) P(打喷嚏|感冒) * P(感冒) / P(建筑工人) * P(打喷嚏)
    P(建筑工人|感冒) = 1/3
    P(打喷嚏|感冒) = 2/3
    P(感冒) = 3/6 = 1/2
    P(建筑工人) = 2/6 = 1/3
    P(打喷嚏) = 3/6 = 1/2

所以

    P(感冒|打喷嚏*建筑工人) = （1/3 * 2/3 * 1/2 ） / （1/3 * 1/2） = 2/3

再取个例2（来自机器学习（周志华））：

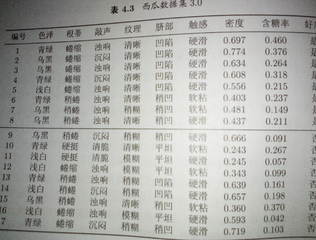
我们要求一个:

根据朴素贝叶斯定理:
我们有
P(好瓜=是|色泽=青绿，根蒂=蜷缩，敲声=浊响，纹理=清晰，脐部=凹陷，触感=硬滑，密度=0.697，含糖率=0.46) =
P(色泽=青绿|好瓜=是) * P(根蒂=蜷缩|好瓜=是) * P(敲声=浊响|好瓜=是) * P(纹理=清晰|好瓜=是) * P(脐部=凹陷|好瓜=是) * P(触感=硬滑|好瓜=是) * P(密度=0.697|好瓜=是) * P(含糖率=0.46|好瓜=是) * P(好瓜=是) / （P(色泽=青绿) * P(根蒂=蜷缩) * P(敲声=浊响) * P(纹理=清晰) * P(脐部=凹陷) * P(触感=硬滑) * P(密度=0.697) * P(含糖率=0.46)）

P(好瓜=是) = 8/17
P(色泽=青绿|好瓜=是) = 3/8
…
（好瓜=是的瓜密度均值为0.574， 方差 = 0.129）
P(色泽=青绿|好瓜=是) = exp(-(0.697-0.574)^2 / 2*0.129)) / sqrt((2*π)*0.129) ≈ 1.959
…

结果P(好瓜=是|色泽=青绿，根蒂=蜷缩，敲声=浊响，纹理=清晰，脐部=凹陷，触感=硬滑，密度=0.697，含糖率=0.46) = 0.038
同理
P(好瓜=否|色泽=青绿，根蒂=蜷缩，敲声=浊响，纹理=清晰，脐部=凹陷，触感=硬滑，密度=0.697，含糖率=0.46) =0.000068

所以分类到好瓜中。

---

拉普拉斯修正(laplace correction)

特别的，如果样本中有，但是训练集中没有，这样就有可能导致分类不合理。
例如在例1 中 如果样本中出现职业一个打喷嚏的学生，那么最后算出来的结果，P(感冒|打喷嚏*学生) = 0,很明显是不对的。

拉普拉斯修正修正原理很简单：设Ni对于分类为c第i个特征属性的可能取到的类别数目
，那么:
P(xi|c) =（ |Dc,xi|+1） / （|Dc|+Ni ）
其中 |Dc,xi| 表示训练集中分类为c的特征属性为xi的数目， |Dc| 表示训练集中分类为c的数目。

在例1 经过修正后

P(建筑工人|感冒) = （1+1）/（3+4） = 2/7

P(打喷嚏|感冒) = （2+1）/（3+2） =3/5

P(感冒) = 3/6 = 1/2

P(建筑工人) = 2/6 =1/3

P(打喷嚏) = 3/6 = 1/2

P(感冒|打喷嚏建筑工人) = P(建筑工人|感冒)P(打喷嚏|感冒) * P(感冒) / P(建筑工人) * P(打喷嚏) = （2/7 * 3/71/2） / （1/31/2） = 2/35

扫码下载CDA数据分析师APP，更多免费精彩内容等你来学！题库

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

分享0 收藏0 回帖

关键词：贝叶斯分类 朴素贝叶斯 机器学习 分类算法 贝叶斯