R in action读书笔记（13）第十章 功效分析

是 否 +2 论坛币

k人 参与回答

经管之家送您一份

应届毕业生专属福利!

求职就业群

赵安豆老师微信：zhaoandou666

经管之家联合CDA

送您一个全额奖学金名额~ !

立即领取

感谢您参与论坛问题回答

经管之家送您两个论坛币！

+2 论坛币

功效分析

功效分析可以帮助在给定置信度的情况下，判断检测到给定效应值时所需的样本量。反过来，它也可以帮助你在给定置信度水平情况下，计算在某样本量内能检测到给定效应值的概率。如果概率低得难以接受，修改或者放弃这个实验将是一个明智的选择。

10.1假设检验速览

在研究过程时，研究者通常关注四个量：样本大小、显著性水平、功效和效应值。样本大小指的是实验设计中每种条件/组中观测的数目。显著性水平（也称为alpha）由I型错误的概率来定义。也可以把它看做是发现效应不发生的概率。功效通过1减去II型错误的概率来定义。我们可以把它看做是真实效应发生的概率。效应值指的是在备择或研究假设下效应的量。效应值的表达式依赖于假设检验中使用的统计方法。

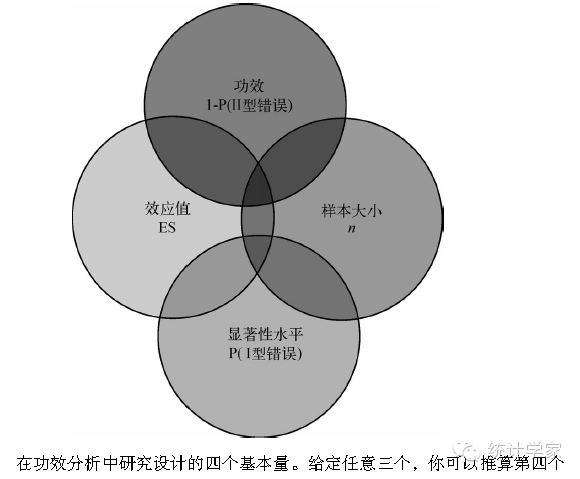
10.2 用pwr 包做功效分析

函 数                 功效计算的对象

pwr.2p.test()     两比例（n相等）

pwr.2p2n.test()   两比例（n不相等）

pwr.anova.test()  平衡的单因素ANOVA

pwr.chisq.test()  卡方检验

pwr.f2.test()     广义线性模型

pwr.p.test()      比例（单样本）

pwr.r.test()      相关系数

pwr.t.test()      t检验（单样本、两样本、配对）

pwr.t2n.test()    t检验（n不相等的两样本）

10.2.1 t 检验

对于t检验，pwr.t.test()函数提供了许多有用的功效分析选项，格式为：

function (n = NULL, d = NULL, sig.level = 0.05, power = NULL,

    type = c("two.sample","one.sample", "paired"), alternative =c("two.sided", "less", "greater"))

n为样本大小。

d为效应值，即标准化的均值之差。d =(m1-m2)/s

sig.level表示显著性水平（默认为0.05）。

power为功效水平。

type指检验类型：双样本t检验（two.sample）、单样本t检验（one.sample）或相依样本t检验（paired）。默认为双样本t检验。

alternative指统计检验是双侧检验（two.sided）还是单侧检验（less或greater）。默认为双侧检验。

>library(pwr)

>pwr.t.test(d=.8,sig.level=.05,power=.9,type="two.sample",alternative="two.sided")

     Two-samplet test power calculation

              n =33.82554

              d =0.8

      sig.level =0.05

          power=0.9

    alternative = two.sided

NOTE: n is number in*each* group

10.2.2 方差分析

pwr.anova.test()函数可以对平衡单因素方差分析进行功效分析。格式为：

function (k = NULL, n = NULL, f = NULL, sig.level =0.05, power = NULL)其中，k是组的个数，n是各组中的样本大小

对于单因素方差分析，效应值可通过f来衡量:

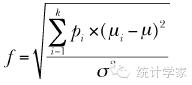
其中，pi = ni/N，

ni = 组i的观测数目

N = 总观测数目

μi

= 组i均值

μ= 总体均值

σ2 = 组内误差方差

> pwr.anova.test(k=5,f=.25,sig.level=.05,power=.8)

     Balancedone-way analysis of variance power calculation

              k= 5 #结果表明，总样本大小为5 × 39，即195

              n= 39.1534

              f= 0.25

      sig.level= 0.05

          power= 0.8

NOTE: n is number in each group

10.2.3 相关性

pwr.r.test()函数可以对相关性分析进行功效分析

function (n = NULL, r = NULL, sig.level = 0.05, power = NULL, alternative = c("two.sided", "less", "greater"))

n是观测数目，r是效应值（通过线性相关系数衡量），sig.level是显著性水平，power是功

效水平，alternative指定显著性检验是双边检验（tow.sided）还是单边检验（less或greater）。

>pwr.r.test(r=.25,sig.level=.05,power=.90,alternative="greater")

    approximate correlation power calculation (arctangh transformation)

              n= 133.2803

              r= 0.25

      sig.level= 0.05

          power= 0.9

alternative= greater

10.2.4 线性模型

对于线性模型（比如多元回归），pwr.f2.test()函数可以完成相应的功效分析，格式为:

function (u = NULL, v = NULL, f2 = NULL, sig.level = 0.05, power = NULL) ，u和v分别是分子自由度和分母自由度，f2是效应值。

当要评价一组预测变量对结果的影响程度时，适宜用第一个公式来计算f2；当要评价一组预测变量对结果的影响超过第二组变量（协变量）多少时，适宜用第二个公式。

> pwr.f2.test(u=3,f2=.0769,sig.level=.05,power=.90)     Multiple regression power calculation               u = 3              v = 184.2426             f2 = 0.0769      sig.level = 0.05          power = 0.9

在多元回归中，分母的自由度等于N - k - 1，N是总观测数，k是预测变量数。本例中，N - 7

- 1 = 185，即需要样本大小N = 185 + 7 + 1 = 193。

10.2.5 比例检验

当比较两个比例时，可使用pwr.2p.test()函数进行功效分析。格式为：

function (h = NULL, n = NULL, sig.level = 0.05, power = NULL,     alternative = c("two.sided", "less", "greater"))

其中，h是效应值，n是各组相同的样本量。效应值h定义如下：

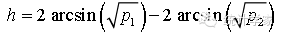
可用ES.h(p1, p2)函数进行计算。

当各组中n不相同时，则使用函数：

function (h = NULL, n1 = NULL, n2 = NULL, sig.level = 0.05, power = NULL, alternative = c("two.sided", "less", "greater")) > pwr.2p.test(h=ES.h(.65,.6),sig.level=.05,power=.9,alternative="greater")     Difference of proportion power calculation for binomial distribution (arcsine transformation)               h = 0.1033347              n = 1604.007      sig.level = 0.05          power = 0.9    alternative = greaterNOTE: same sample sizes

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

分享0 收藏3 回帖

关键词：Action 读书笔记 CTI ACT TIO 读书笔记 action

10.2.6 卡方检验
pwr.chisq.test()函数可以评估卡方检验的功效、效应值和所需的样本大小。格式为：
function (w = NULL, N = NULL, df = NULL, sig.level = 0.05, power = NULL)
其中，w是效应值，N是总样本大小，df是自由度。此处，效应值w如下定义：

p0i = H0时第i单元格中的概率
p1i = H1时第i单元格中的概率
> prob<-matrix(c(.42,.28,.03,.07,.10,.10),byrow=TRUE,nrow=3)
> ES.w2(prob)
[1] 0.1853198
> pwr.chisq.test(w=.1853198,df=2,sig.level=.05,power=.9)
     Chi squared power calculation
              w = 0.1853198
              N = 368.4529
             df = 2
      sig.level = 0.05
          power = 0.9
NOTE: N is the number of observations
10.2.7 在新情况中选择合适的效应值
功效分析中，预期效应值是最难决定的参数。

单因素ANOVA中检测显著效应所需的样本大小
> library(pwr)
> es<-seq(.1,.5,.01)
> nes<-length(es)
> samsize<-NULL
> for(i in 1:nes){
+ result<-pwr.anova.test(k=5,f=es[i],sig.level=.05,power=.9)
+ samsize[i]<-ceiling(result$n)
+ }
> plot(samsize,es,type="l",lwd=2,col="red",
+ ylab="effect size",
+ xlab="sample size (per cell)",
+ main="one way anova with power=.90 and alpha=.05")

10.3 绘制功效分析图形
假设对于相关系数统计显著性的检验，计算一系列效应值和功效水平下所需的样本量，此时可用pwr.r.test()函数和for循环来完成任务检验各种效应值下的相关性所需的样本量曲线
library(pwr)
r<-seq(.1,.5,.01)
nr<-length(r)

p<-seq(.4,.9,.1)
np<-length(p)

samsize<-array(numeric(nr*np),dim=c(nr,np))
for(i in 1:np){
  for(j in 1:nr){
   result<-pwr.r.test(n=NULL,r=r[j],
    sig.level=.05,power=p[i],
   alternative="two.sided")
   samsize[j,i]<-ceiling(result$n)
  }

xrange<-range(r)
yrange<-round(range(samsize))
colors<-rainbow(length(p))
plot(xrange,yrange,type="n",
       xlab="correlationcoefficient (r)",
       ylab="sample size(n)")

for(i in 1:np){
   lines(r,samsize[,1],type="l",lwd=2,col=colors[i])
  }

abline(v=0,h=seq(0,yrange[2],50),lty=2,col="grey89")
abline(h=0,v=seq(xrange[1],xrange[2],.02),lty=2,col="grey89")
title("sanple size ")
legend("topright",title="power",as.character(p),fill=colors)

10.4 其他软件包
asypow 通过渐进似然比方法计算功效
PwrGSD 组序列设计的功效分析
pamm 混合模型中随机效应的功效分析
powerSurvEpi 流行病研究的生存分析中功效和样本量的计算
powerpkg 患病同胞配对法和TDT（TransmissionDisequilibrium Test，传送不均衡检验）设
计的功效分析
powerGWASinteractionGWAS交互作用的功效计算
pedantics 一些有助于种群基因研究功效分析的函数
gap 一些病例队列研究设计中计算功效和样本量的函数
ssize.fdr 微阵列实验中样本量的计算

xie xie

xie xie