虽然几乎每个策略在回测过程中允许犯一些独有的错误,但是有些错误是普遍,适用于所有的市场,有些只与具体的策略有关。
前视偏差
顾名思义,前视偏差意味着你在回测程序里用了明天价格来决定今天的交易信号,或者从更一般的意义上,回测的过程中使用了未来信息来预测当前情况。举一个常见的例子,在回测当天数据时,我们用一天的最高价或最低价作为入场信号。(在结束一天的交易之前,我们是无法确定当天的最高价和最低价的。)前视偏差犯了一个基本的编程错误,它只能影响回测程序而不是实盘程序,因为在实盘过程中是没有办法获取未来信息的。回测和实盘程序的区别为我们指向了避免前视偏差的方法,如果回测和实盘程序是同一个,那么它们之前的区别就只有数据的不同了(历史数据放在前面,实时市场数据放在后面),这样在程序里就不会出现前视偏差了。在本章的后面,我们会了解到哪些平台是允许在回测和实盘上采用相同的代码。
数据透视偏差和线性美
数据透视偏差是由于有太多的自由参数,这些参数过度拟合过去的市场模式,使得策略的历史表现看起来很好。但是这些随机市场模式将来不太可能会重新出现,这造成了过拟合的模式不太可能有太多的预测能力。
总所周知,解决数据透视偏差的方法如下:我们应该用样本外的数据对模型进行检验,然后丢弃掉在表现不好的模型。但这说起来容易做起来难,我们真的愿意放弃可能花费了数周而完成的模型,并且把它扔进垃圾桶?几乎没有多少人会如此的果断。大多数人会使用这种方法或那种方法去调整模型,最后使得模型在样本内和样本外数据都表现良好。但是你瞧,我们刚刚只是把测试数据编程了样本外数据变成了样本内数据!
如果你不愿意扔掉一个模型,仅仅因为它在一个固定的样本外数据集表现不好(毕竟,在样本外数据表现不好可能是正好是运气差)。或者你的数据集比较小,你在调整模型的时候几乎需要用到所有的数据,此时你可以考虑交叉验证的想法。也就是说,你可以选择一些不同的数据子集用来训练和调整模型,更重要的是,要确保模型在这些不同的子集里表现良好。为什么我们偏好于夏普比率较高和最大回撤时间较短的模型,一个原因是这几乎可以确保模型将通过交叉验证检验:模型在唯一的子集检验失败,正好是发生罕见的回撤时间。
有一种普遍的方法去最小化建立交易策略所产生的数据透视偏差:使模型尽可能的简单,尽可能少的参数。许多交易者喜欢第二条原则,但是没有意识到模型只有少量参数但是却有很多复杂的交易规则一样容易受到数据透视偏差的影响。通过两个原则可以得出如下结论:非线性模型比线性模型更容易受到数据透视偏差的影响,因为相比于线性模型,非线性模型不仅更加复杂,而且通常含有更多的独立参数。
假设我们试图通过历史价格序列简单的推断来预测价格,非线性模型肯定更适合这个历史数据,但是这也不能保证它可以更好预测未来。即使我们在非线性模型和线性模型中固定一样的参数个数,我们必须要记住一条,我们通常可以用泰勒展开,类似于微积分,去近似于非线性模型,也是就说一个简单的,线性的模型通常可以近似对应一个非线性模型,以上是一个很好的理由为什么这类线性模型也是不能用的(这些较低阶项消失的奇异情况下的除外,但是这种情况很少用来描述现实中的金融时间序列)。
本文中还有一个同等重要的推论,就是收益率的概率分布,我们经常听到的是高斯分布,但是它未能捕捉金融市场的极端事件。但是除了高斯分布,我们面临着如何在众多的其他分布选择的问题,收益率应该是学生t-分布,可以让我们捕捉到它的偏度和峰度,或者是帕累托分布,完全地分配有限的二次矩?任何选择都有一些武断的因素,这些决定都只是基于有限收益率的观察样本。因此,由奥卡姆剃刀原理表明,如何没有强有力的理论和实证去支持非高斯分布,收益率的概率分布应该假设成高斯形式。
线性模型不仅意味着线性价格预测公式,而且包含线性资本分配公式。假设均值回归模型应用在价格序列,价格的变化dy在下一个时间段dt里,是与均值价格和当前价格之差成正比的:
dy(t)=(λy(t−1)+μ)dt + dε.
这就是所谓的奥恩斯坦-乌伦贝克公式(Ornstein-Uhlenbeck),在第二章我们会详细地说明和展开。通常情况下,交易员会用布林带从价格序列里,通过均值回归来获取利润,也就是超过(低于)某个阈值时,发出卖(买)的指令。然而,如果我们被要求坚持用线性模型,当价格上涨时,我们将被迫发出卖的指令,这样总市值与价格和均值之差成反比。用交易员的专业术语,这叫着“均线回归”或“规模回归”,我们将在第三章讨论这种技术。
细心的你会发现本书的一些例子都是线性模型,因为简单的技术让我们阐明以下这点:利润并非来源于精细的、复杂的聪明策略,而是来自于市场的内在无效性,这种无效性是具有隐蔽性,并非一览无余。不耐心的读者可以直接去看例子4.2,它表示一个线性的均值回归模型,用于交易所指数基金和其组成的一篮子股票;或者例子4.3和4,4,表示的是两个应用于股票的线性多空统计套利策略。
最极端的线性预测模型之一是所以的系数在不同量级都相等(但不一定)。例如,假设你确定一些要素能够有效的预测明天股票指数是上涨的。一个要素可能是今天的收益,今天的收益为正就预测明天的收益也为正。另一个要素可能是今天的波动率指数(VIX)变化情况,VIX减少就预测明天收益为正。你可能有数个这样的要素。如果你通过Z-scores方法标准化这些要素(用在样本数据上):
z(i) = ( f(i) − mean( f ))/std( f ), (1.1)
其中f(i)表示第i个要素,你可以预测明天的收益R,依据如下公式:
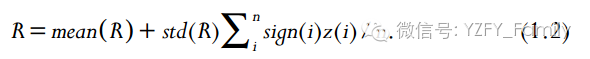
其中mean( f ) 和 std( f )的值分别是历史数据f(i) 的均值和标准方差,sign(i)是f(i)和R的相关性的符号函数,mean(R)和std(R)每日收益率的均值和标准方差。丹尼尔·卡内曼(Daniel Kahneman),诺贝尔经济学奖获得者,在他的畅销书《Thinking, Fast and Slow》写到“分配给所有的预测要素以相等权重的公式是最好的,因为这样不会受到有意外事件的样本的影响”(Kahneman,2011)。等式1.2是一个简化版的用于预测股票回报的一般因子模型。但是它预测股票的绝对收益的时,可能误差很大,也可能非常准确,它预测相对收益时,通常结果都足够好。这意味着,如果我们用来排序股票,然后形成一个多空头组合策略,买入前10%的股票,卖出后10%的股票,投资组合的平均回报率一般都是正期望的。
实际上,如果你的目标只是排名股票而不是达到一个预期回报,有一个比等式1.1和1.2更简单的方法区综合各个因子f 's。我们可以先基于一个因子f(i)计算股票的排名rank(i),然后利用f(i)和预期收益的相关性的符号函数,我们乘以这些排名。最后,我们把这些带有正负号的排名相加:
作为一个例子,Joel Greenblatt 曾用双因子模型去排序股票而闻名,被称为“魔术公式”:f(1)=资本回报率和f(2)=净收益率(Greenblatt, 2006)。假设我们买入前30名的股票,然后持有期为一年,此策略的年化收益率(APR)从1988到2004年为30.8%,相比之下,S&P500的年化收益率为12.4%。这真是线性的胜利!
最后,无论你多么小心地试图阻止数据透视偏差出现在测试过程中,它会莫名其妙地爬进你的模型。
所以最后我们必须执行一个向前走的测试,真正的样本外数据测试。这向前走测试可以以模拟交易的形式进行,但是最好,该模型应该用于实盘交易(即使用最小的杠杆),这样策略的每个方面,甚至在模拟盘都躲避掉的方面都能测试。如果发现实盘交易产生的夏普比率比回测一半还好,对于大部分的交易者都是心满意足的。
![]()
欢迎加入“量化投资宽客”,这里会分享量化策略和最新观点,欢迎您的留言!




 雷达卡
雷达卡





 京公网安备 11010802022788号
京公网安备 11010802022788号







