发帖
雷达卡
阅读原文：http://t.cn/R6tUUJ6
如今,大数据（Big Data）和数据挖掘(Data Mining)成为了一个热门话题和学术研究课题，但很多人对于它们的定义却只停留在数据量庞大而造成计算困难的层面。实际上，大数据往往代表的是大量的、不完全的、有噪声的、模糊的数据，而数据挖掘是指从大数据中提取隐含的、事先不知道的、但又是潜在有用的信息和知识的过程。
决策树算法作为数据挖掘其中一种判定数据所属类别的算法，数学模型简单，编程有程序包，极易上手，适合大家研究使用。具体应用常常是针对股票的高频数据算出VWAP后对股票涨跌进行预测，VWAP数据我注意到京东平台提供了，用get_vwap(intervals, frequency='day')语句在策略里就可以。需要前期的训练数据集进行学习。通常使用Python中的Scikit-learn学习包（简称sk-learn）。
首先我们需要了解一种衡量信息含量的指标：信息熵，以及决策树的几种经典的基于信息熵的算法：ID3算法,C4.5算法和CART算法。
上世纪40年代末，香农提出了“信息熵”的概念，他用信息熵的概念来描述信源的不确定度。信息熵越大代表信息越混乱，而我们需要的是由从大数据混乱的信息获得稳定的信息，因此我们预想的是在提取信息过程中看到信息熵由大变小。定义式中，P+代表正向事件发生概率，P-代表负向事件发生概率，比如:正向事件代表股票上涨，负向代表股票下跌。
由于我们希望提取的信息越来越趋于稳定，越来越明确，我们需要定义“信息的增益”的计算方式：
举个例子：天气中的很多因素（如：湿度、风力）可能影响能不能在该天气下进行网球比赛，如下图所示。
Outlook代表天气的大体状况，比如晴天、阴天、下雨等，Humidity代表空气湿度，Wind代表风力强度等等。
原始信息为：在观测数据的14天中，9天可以进行网球比赛，5天不能，记为：S=[9+,5-]。计算原始信息熵为：
风力信息中有两类，strong（风力大）和weak（风力小）。
风力为Strong的6天中，3天可以打球,3天不可以，记为S(strong)=[3+,3-]。
同理记为：S(weak)=[6+,2-]
计算添加风力的信息后的信息熵为：
最终计算风力的信息增益：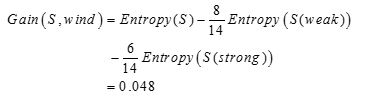
同理，计算温度、湿度、天气大体情况的信息增益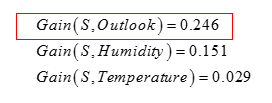
依照熵增益的大小，我们优先用Outlook（天气大体情况）对当天所有的天气信息进行能不能进行网球比赛的类别判断，其次用Humidity（湿度）高低，再来用Wind（风力强弱），最后用Temperature（天气温度高低）。我们可以用如下的示意图表示这个决策树（图中省略了天气温度这一影响）：
ID3算法
ID3算法的核心是在决策树的各个结点上应用信息增益准则进行特征选择。具体做法是：
从根节点开始，对结点计算所有可能特征的信息增益，选择信息增益最大的特征作为结点的特征，并由该特征的不同取值构建子节点；
对子节点递归地调用以上方法，构建决策树；
直到所有特征的信息增益均很小或者没有特征可选时为止。
想了解关于C4.5算法跟CART 算法请点击阅读原文同时附上算法的源代码图
阅读原文：http://t.cn/R6tUUJ6
京公网安备 11010802022788号
