发帖
雷达卡
相信大家都会求导吧，给定一个f(x)，都可以唯一确定一个导函数f '(x)，导函数给出了原函数的变化情况。
比如
导函数为
但是，倒过来就不行了，一个导函数对应原函数为，
，
………无穷多个。
写成积分形式就是
具体求导过程很多，自己看，为什么呢，因为在求导的过程中，我们虽然得到的函数今后的变化情况，但损失了一部分信息，就是原函数的初始值。概括一下，
原函数的信息=导函数的信息+初始值信息，
初始值信息没了，一个导函数就对应多个原函数了。
知道了原因，我们就可以去掉上面那个恼人的C了，加入初始值信息就好了。
那个f（0）就是初始信息。当然初始信息可以从任意位置开始，不一定从0开始
这时候我们得到了
(原函数的信息=导函数的信息+初始值信息)
继续这个过程
代入得
再接着做下去
无限做下去，前面是余项，整个是泰勒展开式
泰勒公式
公式描述：泰勒公式可以用若干项连加式来表示一个函数，这些相加的项由函数在某一点的导数求得。
在泰勒公式中，取x0=0，得到的级数
称为麦克劳林级数。函数
的麦克劳林级数是x的幂级数，那么这种展开是唯一的，且必然与
的麦克劳林级数一致。
也就是：泰勒公式：
常见的麦克劳林级数下面给出几个常见函数在x=0处的泰勒级数，即麦克劳林级数。
指数函数：
自然对数：
几何级数：
正弦函数：
余弦函数：
正切函数:
更多内容参考：https://www.zhihu.com/question/21149770
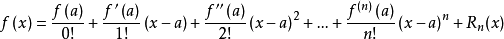
京公网安备 11010802022788号
