谈点哲学

相似文件 换一批

是 否 +2 论坛币

k人 参与回答

经管之家送您一份

应届毕业生专属福利!

求职就业群

赵安豆老师微信：zhaoandou666

经管之家联合CDA

送您一个全额奖学金名额~ !

立即领取

感谢您参与论坛问题回答

经管之家送您两个论坛币！

+2 论坛币

近代哲学有两个派别——英国经验主义和欧陆理性主义。各自用一句口号来代表的话，一个是“一切知识都要从经验中得出”，另一个是“理性高于经验”。前一句口号好理解，后一句口号怎么理解？

譬如平面三角形内角和等于180°，这个知识无需任何经验就可以通过推理得出来。假如你拿着个量角器测量平面三角形的内角，然后加总起来发现不等于180°，那么肯定是你的测量实践错了，而不可能是几何定理错了。这么说起来，难道真理是检验实践的标准？

莱布尼茨把真理分成两种，一种叫推理的真理，或者叫逻辑真理，例如几何定理，是必真的。另一种叫事实真理，是从经验中得来，仅仅有可能是真的，所以叫或然真理。例如“所有的天鹅都是白的。”

但是且慢，几何定理是从几何公理推理出来的，几何公理打哪来？穆勒认为，几何公理也是从经验中总结出来的。假如穆勒是对的，那么几何公理岂不是也变成了“所有的天鹅都是白的”一样的“事实真理”，有朝一日我们发现了黑天鹅，那么几何公理会不会不成立？

19世纪俄罗斯有个数学家叫罗巴切夫斯基，他发了狠要把欧氏几何公理“证明”出来。怎么证呢？用反证法——假定过直线外一点，能做两条以上平行线，如果能证明这个假设不成立，那不就能证明“过直线外一点有且只有一条平行线”了么。结果意外地发现，两条以上平行线的假设完全可以成立。德国数学家黎曼则另辟蹊径，假设所有的直线都相交（没有平行线），也得到一套自洽的几何学。他俩的工作打开了一扇大门——非欧几何。罗巴切夫斯基也因此被人们尊为“几何学中的哥白尼”。

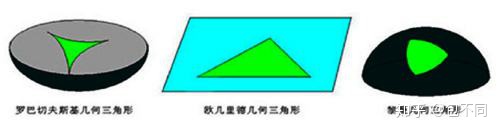
在今天看来，可以认为几何公理是定义——欧氏公理定义欧氏空间，罗氏公理定义罗氏空间，黎曼公理定义黎曼空间。在罗氏空间里，三角形内角和小于180°，在黎曼空间里，三角形内角和大于180°。

你可能会觉得，不对啊，罗氏空间是负曲率，黎曼空间是正曲率，欧氏空间是曲率为零的平面，那么我要问了，你怎么定义“平”面？你怎么知道一个面的曲率是零？......???！小心不要掉进循环论证的套套里去哦~

有一种“经验”上的判断“平”的方法，就是直接用眼睛瞄，这是因为通常我们假定光走直线，如果光可以不走直线的话呢？我们如何知道自己是不是处在一个大鱼缸内，看到的东西都受到了扭曲呢？（霍金在《大设计》中提出的有趣问题）

广义相对论的大意是把引力问题变成几何问题，说我们所处的空间是四维的，而且还是弯曲的，我们看到的三维世界只是一个投影。这个情形很难想象，大约像把地球投影到地图，航空公司的飞行线路总是选择“两点间最短的距离”（关于直线的定义或公理）——在球面上两点间最短距离是“大圆”（通过球心的平面和球面的交线），赤道、经线都是大圆，纬线可不是大圆，所以球面上“两点间最短的距离”在二维的平面地图上看起来就是条曲线。

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

那么，为啥说我们生活的空间是四维弯曲的呢？其实数学家可以任意定义空间，100维，200维都可以，物理学家觉得
哪套定义好用就用哪套——开普勒觉得正圆不好用就用椭圆，爱因斯坦觉得欧氏的不好用就用黎曼的（球面几何），霍金觉得10维不够用就用11维的。关键的关键，是要能通过经验的检验。

近两年的“引力波”、“第一张黑洞照片”都是对广义相对论的大考，每当它通过一次大考，都增添了我们对这个理论的信心。而牛顿引力理论，通过了天王星、海王星轨道大考（发现了海王星、冥王星），但是没有通过水星轨道大考，这时候我们就要琢磨一下是不是需要修正理论了。

所以，实践才是检验真理的唯一标准，经验高于理性！

康德把命题分为两类“分析”与“综合”。

谓词概念包含于主词之中的叫做分析判断。谓词概念不包含于主词之中的叫做综合判断。

例：
“所有的单身汉都未婚。”单身汉的定义是未婚的男人，“未婚”概念已经包含在了“单身汉”的概念当中，这是一个分析判断。分析判断可以帮助我们推理出无矛盾的结论，譬如“有些单身汉是结了婚的”就不成立。

“所有的天鹅都是白色的。”主词“天鹅”里面并不包含“白色”的概念，需要综合事实来判断，所以叫综合判断。

那么数学和几何学呢？

“平面上三角形的内角和等于180°”这个判断中，“三角形的内角和等于180°”已经蕴含于"平面”的定义（欧氏公理）当中，所以它是一个分析判断！

在数学方面，数学家罗素在《西方哲学史》中写到：

......以上所谈的工作的一个结果是，剥夺了自从毕达哥拉斯和柏拉图以来数 学一直占据的崇高地位，并且打破了从数学得来的那种反对经验主义的臆断根据。的确，数学知识不是靠由经验进行归纳获得的；我们相信 2 加 2 等于 4，其理由并不在于我们凭观察极经常发现到两件东西跟另外两件东西合在一 起是四件东西。在这个意义上，数学知识依然不是经验的知识。但也不是关 于世界的先验知识。其实，这种知识仅仅是词句上的知识。“3”的意思是“2 ＋1”，“4”的意思是“3＋1”。由此可见（固然证明起来很长）“4”和“2 ＋2”指一个意思。因而数学知识不再神秘。它和一码有三呎这个“天经地义” 完全属同样的性质。

我们来看看康德在《纯粹理性批判》里面是咋说的：

I.纯粹知识和经验性知识的区别
我们的一切知识都从经验开始，这是没有任何怀疑的；因为，如果不是通过对象激动我们的感官，一则由它们自己引起表象，一则使我们的知性活动运作起来，对这些表象加以比较，把它们连结或分开，这样把感性印象的原始素材加工成称之为经验的对象知识，那么知识能力又该由什么来唤起活动呢？所以按照时间，我们没有任何知识是先行于经验的，一切知识都是从经验开始的。但尽管我们的一切知识都是以经验开始的，它们却并不因此就都是从经验中发源的。因为很可能，甚至我们的经验知识，也是由我们通过印象所接受的东西和我们固有的知识能力（感官印象只是诱因）从自己本身中拿来的东西的一个复合物，对于我们的这个增添，直到长期的训练使我们注意到它并熟练地将它分离出来以前，我们是不会把它与那些基本材料区分开来的。

这样，至少就有一个还需要进一步研究而不能一见之下马上打发掉的问题：是否真有这样一种独立于经验、甚至独立于一切感官印象的知识。人们把这样一种知识称之为先天的（a priori），并将它们与那些具有后天的（a posteriori）来源、即在经验（Erfahrung）中有其来源的经验性的（empirische）知识区别开来。

然而“先天的”这个术语还不足以确定地表示与上述问题相适合的全部意义。因为很有些出自经验来源的知识，我们也习惯于说我们能够先天地产生它或享有它，因为我们不是直接从经验中、而是从某个普遍规则中引出这些知识来的，但这个规则本身又仍然还是借自经验的。所以我们会说一个在挖自己房子基础的人：他本可以先天地知道房子要倒，即他不必等到这房子真的倒下来的经验。但他毕竟还不能完全先天地知道这件事。因为他事先总归要通过经验才得知，物体是有重量的，因而若抽掉它们的支撑物它们就会倒下来。

所以我们在下面将把先天的知识理解为并非不依赖于这个那个经验、而是完全不依赖于任何经验所发生的知识。与这些知识相反的是经验性的知识，或是那些只是后天地、即通过经验才可能的知识。但先天知识中那些完全没有掺杂任何经验性的东西的知识则称为纯粹的。于是，例如“每一个变化都有其原因”这个命题是一个先天命题，只是并不纯粹，因为变化是一个只能从经验中取得的概念。

Ⅱ.我们具有某些先天知识，甚至普通知性也从来不缺少它们
在这里，关键是要有一种我们能用来可靠地将一个纯粹知识和经验性的知识区别开来的标志。经验虽然告诉我们某物是如此这般的状况，但并不告诉我们它不能是另外的状况。因此首先，如果有一个命题与它的必然性一起同时被想到，那么它就是一个先天判断；如果它此外不再由任何别的命题引出，除非这命题本身也是作为一个必然命题而有效的，它就是一个完全先天的命题。其次，经验永远也不给自己的判断以真正的或严格的普遍性，而只是（通过归纳）给它们以假定的、相比较的普遍性，以至于实际上我们只能说：就我们迄今所觉察到的而言，还没有发现这个或那个规则有什么例外。所以，如果在严格的普遍性上、亦即不能容许有任何例外地来设想一个判断，那么它就不是由经验中引出来的，而是完全先天有效的。而经验性的普遍性只是把对大多数场合下适用的有效性任意提升到对一切场合都适用的有效性，例如在这样一个命题中：一切物体都有重量；相反，在严格的普遍性本质上属于一个判断的场合，这时这种普遍性就表明了该判断的-一个特别的知识来源，也就是一种先天的认识能力。于是，必然性和严格普遍性就是一种先天知识的可靠标志，而两者也是不可分割地相互从属的。但由于在两者的运用中，有时指出判断的经验性的局限比指出判断中的偶然性要更容易一些，又有些时候指出我们加在一个判断上的无限制的普遍性比指出这个判断的必然性要更明白一些，所以不妨把上述两个标准分开来使用，它们每一个就其自身说都是不会出错的。

不难指出，在人类知识中会现实地有这样一些必然的和在严格意义上普遍的、因而纯粹的先天判断。如果想从科学中举一个例子，那么我们只须把目光投向一切数学命题；如果想从最普通的知件使用中举这样一个例子，则在这方面可引用“一切变化都必有一个原因”这个命题；的确，在后一个例子中，原因这个概念本身显然包含着与一个结果相连结的必然性的概念，以及规则的严格普遍性的概念，以至于，如果我们像休谟所做的那样，想要把这个概念从发生的事经常地与在先的事相伴随中，从由此产生的连结诸表象的习惯（因而仅仅是主观的必然性）中引申出来，那么这个概念就会完全失去了。我们甚至无须这样一些例子来证明我们知识中那些先天纯粹原理的现实性，也可以阐明这些原理对于经验本身的可能性是不可或缺的，因而阐明其先天性。因为假如经验所遵循的一切规则永远总是经验性的、因而是偶然的，经验又哪里还想取得自己的确定性；所以我们很难把这些规则当作第一原理来看待。只是在这里，我们可以满足于摆明了我们认识能力的纯粹运用这一事实以及这种运用的标志。但这样一些先天原理的根源不仅仅在判断中，而且甚至在概念中也表现出来了。如果你从物体这个经验概念中把它的颜色、硬或软、重量、甚至不可入性这一切经验性的东西都一个个地去掉，这样最终留下的是它（现在已完全消失了）所占据的空间，而这是你不能去掉的。同样，如果你从任何-一个有形的或无形的对象的经验性概念中把经验告诉你的一切属性都去掉，你却不可能取消你借以把它思考为实体或依赖于一个实体的那种属性（虽然实体这个概念比一般客体这个概念包含更多的规定）。这样，由于这个概念借以强加于你的这样一种必然性所提供的证据，你就不得不承认这概念在你的先天认识能力中有自己的位置。

Ⅲ.哲学需要一门科学来规定一切先天知识的可能性、原则和范围

略

Ⅳ分析判断与综合判断的区别
略

V.在理性的一切理论科学中都包含有先天综合判断作为原则
1.数学的判断全部都是综合的。这条定理似乎至今尚未被人类理性的分析家们注意到，甚至恰好与他们的一切推测相反，尽管它具有无法反驳的确定性并有非常重要的后果。这是因为，人们由于看到数学家的推论全都是依据矛盾律进行的（这是任何一种无可置疑的确定性的本性所要求的），于是就使自己相信，数学原理也是出于矛盾律而被承认的；他们在这里是弄错了；因为，一个综合命题固然可以根据矛盾律来理解，但只能是这样来理解，即有另外一个综合命题作为前提，它能从这另外一个综合命题中推出来，而决不是就其自身来理解的。

首先必须注意的是：真正的数学命题总是先天判断而不是经验性的判断，因为它们具有无法从经验中取得的必然性。但如果人们不愿接受这一点，那么好，我将把自己的命题局限于纯粹数学，这一概念的题中应有之义是：它不包含经验性的知识，而只包含纯粹的先大知识。

虽然人们最初大约会想：7+5=12这个命题是一个单纯分析命题，它是从7加5之和的概念中根据矛盾律推出来的。然而，如果人们更切近地考察一下，那么就会发现，7加5之和的概念并未包含任何更进一步的东西，而只包含这两个数结合为一一个数的意思，这种结合根本没有使人想到这个把两者总合起来的惟一的数是哪个数。12这个概念决不是由于我单是思考那个7与5的结合就被想到了，并且，不论我把我关于这样一个可能的总和的概念分析多么久，我终究不会在里面找到12。我们必须超出这些概念之外，借助于与这两个概念之一相应的直观，例如我们的五个手指，或者（如谢格奈在其《算术》中所说的①）五个点，这样一个一个地把直观中给予的五的这些单位加到七的概念上去。因为我首先取的是7这个数，并且，由于我为了5这个概念而求助于我的手指的直观，于是我就将我原先合起来构成5这个数的那些单位凭借我手指的形象一个一个地加到7这个数上去，这样就看到12这个数产生了。要把5加在7之上，这一点我虽然在某个等于7+5的和的概念中已经想到了，但并没有想到这个和等于12这个数。所以算术命题永远都是综合的；对此我们越是取更大的数目，就越是看得更清楚，因为这样一来就明白地显示出，不论我们怎样把我们的概念颠来倒去，我们若不借助于直观而只借助于对我们的概念作分析，是永远不可能发现这个总和的。

同样，纯粹几何学的任何一个原理也不是分析性的。两点之间直线最短，这是一个综合命题。因为我的直的概念决不包含大小的概念，而只包含某种性质。所以“最短”这个概念完全是加上去的，而决不能通过分析从直线这个概念中引出来。因此在这里必须借助于直观，只有凭借直观这一综合才是可能的。①在这里，通常使我们以为这种无可置疑的判断的谓词已经寓于我们的概念之中、因而该判断似乎就是分析性的那种信念，只不过是用语含混所致。因为我们应该在一个给予的概念上再想出某个谓词来，而这种必要性已经附着于那些概念身上了。但问题不在于我们应该想出什么来加在这个给予的概念上，而在于我们在这个概念中实际上想到了什么，即使只是模糊地想到了什么，而这就表明，这谓词虽然必然地与那概念相联系，但并非作为在概念本身中所想到的，而是借助于某个必须加在这概念上的直观。

几何学作为前提的少数几条原理虽然确实是分析的，并且是建立在矛盾律之上的；但它们正如那些同一性命题一样，也只是用于方法上的连接，而不是作为原则，例如a=a，即全体与自身相等，或（a+b）>a，亦即全体大于其部分。并且即算是这些原理本身，尽管仅仅按照概念来说就是有效的，但它们在数学中之所以行得通，也只是因为它们能在直观中体现出来。

2.自然科学（物理学）包含先天综合判断作为自身中的原则。我只想举出两个定理作例子，一个定理是：在物质世界的一切变化中，物质的量保持不变；另一个定理是：在运动的一切传递中，作用和反作用必然永远相等。显然，在这两个命题上，不仅仅存在着必然性，因而其起源是先天的，而且它们也是综合命题。因为在物质概念中我并没有想到持久不变，而只想到物质通过对空间的充满而在空间中在场。所以为了先天地对物质概念再想出某种我在它里面不曾想到的东西，我实际上超出了物质概念。因此这条定理不是一个分析命题，而是综合的，但却是先天被想到的，而且自然科学纯粹部分的其他一些定理也都是如此。

3.在形而上学中，即使我们把它仅仅看作一门至今还只是在尝试、但却由于人类理性的本性而不可缺少的科学，也应该包含先天综合的知识，并且它所关心的根本不是仅仅对我们关于事物的先天造成的概念加以分解、由此作出分析的说明，相反，我们要扩展我们的先天知识，为此我们必须运用这样一些原理，它们在被给出的概念上增加了其中不曾包含的某种东西，并通过先天综合判断完全远远地超出了该概念，以至于我们的经验本身也不能追随这么远，例如在“世界必然有一个最初的开端”等命题中那样，所以形而上学至少就其目的而盲是由纯粹先天综合命题所构成的。

总是有人说康德哲学深奥难懂，其实无非就是他喜欢用长句子么（据说演讲要有说服力最好用短句），我把它裁裁短：

虽然一切的知识是从经验“开始”（注意不是“得出”），但是有可能“感官现象只是诱因”，我们已经有了个先天的“固有的知识能力”，需要经过“长期的训练使我们注意到它并熟练地将它分离出来”，这就是“纯粹的先天判断”。“如果想从科学中举一个例子，那么我们只须把目光投向一切数学命题......"

"数学的判断全部都是综合的。"

"纯粹几何学的任何一个原理也不是分析性的。"
......

有了前面的预备知识，很容易看出来康德错哪了吧？就像一个著名的脑筋急转弯问题：1+1在什么情况下等于3？答：在算错的情况下。这很好理解是不是？顺着这个思路你再读一遍康德的这段话：

同样，纯粹几何学的任何一个原理也不是分析性的。两点之间直线最短，这是一个综合命题。因为我的直的概念决不包含大小的概念，而只包含某种性质。所以“最短”这个概念完全是加上去的，而决不能通过分析从直线这个概念中引出来。因此在这里必须借助于直观，只有凭借直观这一综合才是可能的。在这里，通常使我们以为这种无可置疑的判断的谓词已经寓于我们的概念之中、因而该判断似乎就是分析性的那种信念，只不过是用语含混所致。因为我们应该在一个给予的概念上再想出某个谓词来，而这种必要性已经附着于那些概念身上了。但问题不在于我们应该想出什么来加在这个给予的概念上，而在于我们在这个概念中实际上想到了什么，即使只是模糊地想到了什么，而这就表明，这谓词虽然必然地与那概念相联系，但并非作为在概念本身中所想到的，而是借助于某个必须加在这概念上的直观。

是不是超级好理解——康德全说反了，而且反得非常彻底，这么一大段话，居然每一句话都能说反掉，我也是醉了。正所谓“以其昏昏，使人昭昭”。

假如你硬要从正面角度去理解1+1=3，我觉得一定会理解得很辛苦，并且有可能会对大脑造成不可恢复的创伤。

康德在《纯理批判》第二版序言中写了这么一段话：

向来人们都认为，我们的一切知识都必须依照对象；但是在这个假定下，想要通过概念先天地构成有关这些对象的东西以扩展我们的知识的一切尝试，都失败了。因此我们不妨试试，当我们假定对象必须依照我们的知识时，我们在形而上学的任务中是否会有更好的进展。这一假定也许将更好地与所要求的可能性、即对对象的先大知识的可能性相一致，这种知识应当在对象被给予我们之前就对对象有所断定。这里的情况与哥白尼的最初的观点是同样的，哥白尼在假定全部星体围绕观测者旋转时，对天体运动的解释已无法顺利进行下去了，于是他试着让观测者自己旋转，反倒让星体停留在静止之中，看看这样是否有可能取得更好的成绩。现在，在形而上学中，当涉及到对象的直观时，我们也能够以类似的方式来试验一下。如果直观必须依照对象的性状，那么我就看不出，我们如何能先天地对对象有所认识；但如果对象（作为感官的客体）必须依照我们直观能力的性状，那么我倒是完全可以想像这种可能性。

人家罗巴切夫斯基”几何学中的哥白尼“是被世人所推崇的，康德可倒好，自封了个哥白尼，所谓”认识论中的哥白尼革命“就是这么炮制出来的。

康德企图回答休谟怀疑论——科学理论怎么可能是真理呢？在今天来看，科学理论的确不是真理啊，牛顿引力说在天文学中已经被广义相对论所取代，早就没人用那玩意了。康德用了个排除法——只有酱紫，科学理论才有可能是真理——把需要回答的问题当成展开论证的前提，而且还把前提全说反了，《纯粹理性批判》就变成了纯粹的扯淡。

难怪罗素在《西方哲学史》中评价康德说：”休谟通过对因果性概念的批判，把他从独断的睡梦中唤醒过 来——至少他这样讲；但是唤醒只不过是暂时的，他不久就发明了一种让他能够再入睡的催眠剂。“

哲学问题大体上可以归为三类：

本体论——世界的本原是什么？

认识论——我们如何去认识世界？

伦理——我们应该怎么做？

每一类问题里面都有对立的两个派别。

本体论里有中世纪唯名论和实在论的对立；

认识论里有英国经验主义和欧陆理性主义的对立；

伦理里面有康德的直觉主义（又叫绝对主义）和边沁的功利主义。

我们学到的唯心主义和唯物主义，属于欧陆理性主义下的分支，把英国经验主义哲学强行纳入到这个划分框架中来，必然会有一定程度的曲解。譬如乔治.贝克莱，通常被我们归为唯心主义者，而且还是非常极端的那种。但实际上他是个唯经验论者，根本就不承认有“第一性的性质”存在，从来也没说过“意识第一性，物质第二性”这样的话。

贝克莱敏锐地注意到：我们能经验到的仅仅是运动，牛顿力学理论是我们经验背后的一个“隐秘的形而上学解释“，而不是什么客观规律。贝克莱哲学解放了思想，为“时空弯曲说”取代“引力说”打开了方便之门，所以波普尔称“贝克莱是马赫和爱因斯坦的先驱"，“使我们免受不容置疑的第一前提之害”。——你说这是唯心主义还是唯物主义？你要说它是唯心主义，那么现代科学——相对论、量子力学——都是唯心主义，唯物主义岂不成了反科学的东西？

不过，我们文革的时候的确曾经把相对论当成唯心主义学说来批判过，刘慈欣的《三体》里的一些情节与此有关。

科学也叫“自然哲学”，属于认识论下面的一个分支——基于经验认识世界的方法。

近代科学思想的启蒙始于弗朗西斯.培根，他主张：一切知识都要从经验中得出——“我们不应该像蚂蚁，单只收集；也不可像蜘蛛，只从自己肚里抽出丝；而应像蜜蜂，既采集、又整理，这样才能酿出香甜的蜂蜜来。”

在培根看来，传统学术的毛病例如他在旧大学中所目睹的也正是经院哲学所特有的那种毛病：依赖寥寥几本古籍，反来复去地对它们的内容作逻辑的修补，而不是注意事物本身。他继续说道：“这种蜕变的学术主要在经院哲学家中间盛行。这些人智慧敏锐而出众，他们有充裕的闲暇，阅读种类不多的书籍，但是他们的智慧禁锢在少数几个作者（主要是他们的独尊者亚里士多德）的窠穴里，因为他们的人身就束缚在修道院和学院的小天地里；他们对自然史和历史都不甚了了，因而他们没有研究大量的问题，而是无限制地发挥智慧，把在他们的书本上苦心编织成的学术之网来束缚我们。因为如果人的智慧和心灵对问题（它是对上帝创造物的沉思）进行工作，那末它们是在按照材料进行工作，因此是有限的；但如果它们是在对自己进行工作，象蜘蛛织网那样，那末便是无限的，它们实际上编织出了学术的蜘蛛网，网丝和编织之精细令人赞叹，但却是空洞的或无益的”


这段议论放在康德身上非常合适，虽然他的”哥白尼革命“具有一定的原创性。

那么，如何从经验中提取出科学理论呢？培根给出了他的方法：带三个表——存在表（正相关），缺乏表（负相关），程度表（量化分析）。这是科学归纳法的雏形，并由此产生了归纳问题。休谟发现，这里面存在两个跳跃——从个别到普遍，从过去到将来——得不到解释。从前面贝克莱对牛顿理论的质疑可以看出，休谟与贝克莱是一脉相承的，他是个极端的怀疑论者。而科学精神的本质就是怀疑！

休谟归纳难题究竟应该如何解决？

先问是不是，再问如何解决。

科学知识是归纳出来的吗？科学知识是归纳出来的吗？科学知识是归纳出来的吗？重要的问题问三遍

为什么全世界那么多天文学家都没归纳出广义相对论，却被一个瑞士专利局的小职员归纳出来了？通过什么实验能归纳出来广义相对论？又通过什么实验能归纳出来万有引力论？通过对行星周日轨道的观测，能同时归纳出万有引力论和广义相对论两套理论吗......

仔细想想，科学知识好像不是归纳出来的吧~

那么，科学知识到底是怎么来的？爱因斯坦到底是怎么鼓捣出广义相对论的？你问谁？当然是爱因斯坦本人啊，他最有资格回答这个问题了对不对？我们来看看他咋说：

“要我们对什么是科学得出一致的理解，实际上并不困难。科学就是一种历史悠久的努力，力图用系统的思维，把这个世界中可感知的现象尽可能彻底地联系起来。说得大胆点,它是这样一种企图：要通过构思过程，后验(posterior)地来重建存在。”——《科学和宗教》1940
“静电学作为一个极限情况包含在电动力学中；在场不随时间而改变的情况下，电动力学的定律就直接得出静电学的定律。任何物理理论都不会获得比这更好的命运了，即一个理论本身指出创立一个更力全面的理论的道路，而在这个更为全面的理论中，原来的理论作为一个极限情况继续存在下去。”——《狭义与广义相对论浅说》

简单来说，科学理论都是猜想，用来解释“可感知的现象”。它遵循这样一套规则——假设旧的科学理论能解释现象P1~Pn，新的科学理论不仅能包容旧理论能够解释的现象，还能解释旧理论解释不了的新现象Pn+1，那么就算KO成功，这个Pn+1就被称为判决性实验。旧理论的地位下降为特例，可以“作为一个极限情况继续存在下去”。新的理论向下兼容，它把现象P1~Pn和现象Pn+1更加“彻底地联系起来”。

换而言之，科学理论不是“归纳”出来的，而是“进化”出来的。科学精神的本质是怀疑！通过不断地怀疑、挑战旧理论而取得进步。

先有猜想还是先有实验，这不是一个先有鸡还是先有蛋的问题。

爱因斯坦在挑战经典物理学的时候，是没有“判决性实验”支持的（旧的实验证据与经典理论和相对论都不矛盾）。是根据新的猜想，设计了检测镭盐质量衰减、日食星光偏侧等等实验来挑战旧理论。

在经典物理理论领域同样如此，亚里士多德曾经断言物体受到外力运动，外力停止，运动停止。伽利略为啥不跑到大街上去观察，从最普遍的现象中“归纳”运动规律，而是有针对性地设计出了斜坡实验？

第谷积累了那么多天文观测数据，为什么没有“归纳”出行星运动三定律而要等到开普勒来完成这项工作？开普勒也不是“归纳”出行星运动定律的，而是经过无数次错误的尝试之后，用椭圆曲线来解释才获得成功。这不是归纳法而是试错法，是大胆地假设小心地求证，是从无数个错误的猜想当中提炼出一个相对靠谱些的猜想的过程。

进化论我们懂，物竞天择，适者生存。首先要有变异——对于思想来说就是要有异见——我们不一样，老天才有得选，我们都一样，你让老天选个几把？

一旦思想被统一，那么科学前进的脚步就会停止，只有解放思想，科学才能进步！

爱因斯坦在《自由和科学》（1940）中写道：

“科学进步的先决条件是不受限制地交换一切结果和意见的可能性一—在一切脑力劳动领域里的言论自由和教学自由。我所理解的自由是这样的一种社会条件：一个人不会因为他发表了关于知识的一般和特殊问题的意见和主张而遭受危险或者严重的损害。交换的自由是发展和推广科学知识所不可缺少的；这件事有很大的实际意义。首先它必须由法律来保障。但单单靠法律还不能保证发表的自由；为了使每个人都能表白他的观点而无不利的后果，在全体人民中必须有一种宽容的精神。这种外在的自由的理想是永远不能完全达到的，但如果要使科学思想、哲学和一般为创造性思想得到尽可能快的进步，那就必须始终不懈地去争取这种自由。”

所以，休谟归纳问题不存在！那些说得有鼻子有眼的归纳问题解决方案都是扯淡。

培根三表法在逻辑上是不完整的，我们并不是随机地观察、总结，而是有目的的设计实验、挑战。只有爱因斯坦这样的科学理论原创者才能清晰、完整地体验到这个过程。

而我们在学校里学习知识的时候，是通过重复前人的某些实验获得某些理论，并由此产生了“知识是从实验和观察中归纳出来”的心理错觉。

实践其实是检验真理的唯一标准。因为所谓真理，从来都只是这个宇宙在某种特定条件下的具体表现，都有其限制条件——譬如物体在粒子尺度，要遵循量子物理；到了正常尺度，就得遵循牛顿定律；而到了宇宙天体的宏观尺度，就得改成相对论了。我们不能说真理有错，只是真理有前提。