频数分布统计与分析
频数分布分析主要通过频数分布表、条形图和直方图,以及集中趋势和离散趋势的各种统计量来描述数据的分布特征。
集中趋势的常用统计量
均值:平均值,但易受极端值的影响。
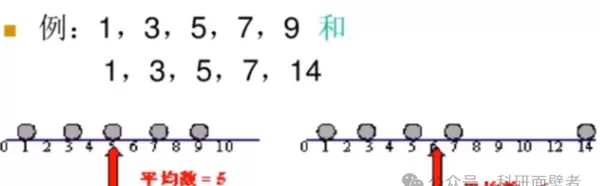
中位数:作为重要的中心度量位置,当数据集为奇数时,排序后最中间的数据即为中位数;若为偶数,则排序后中间两个数据的平均值为中位数。
众数:指出现频率最高的数值,可能不唯一。
离散趋势的常用统计量
方差:用于衡量数据的波动程度,方差越小,表明数据越稳定;方差越大,数据波动越大。
若 \(x_1, x_2, x_3, \ldots, x_n\) 的平均数为 \(M\),则方差公式可表示为:
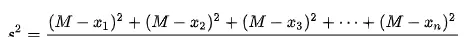
标准差:方差的算术平方根,标准差越大,说明数据分布越分散。
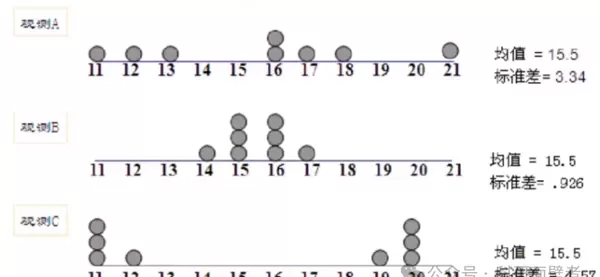
范围:数据的最大值与最小值之差。
正态分布
正态分布图如下所示,该分布有两个参数:期望 μ 和标准差 σ。若随机变量 X 服从一个数学期望为 μ、方差为 σ 的正态分布,记作 N(μ, σ)。其概率密度函数由正态分布的期望值 μ 决定其位置,标准差 σ 决定分布的幅度。当 μ = 0, σ = 1 时,该分布被称为标准正态分布。
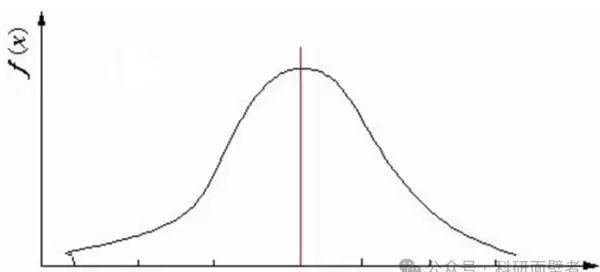
正态分布情况下的偏度和峰度
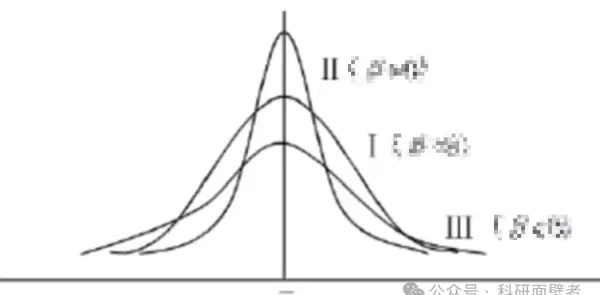
峰度:描述数据分布形态的陡峭程度。峰度的取值范围为 [1, +∞),完全服从正态分布的数据峰度值为 3,峰度值越大,概率分布图越高尖;峰度值越小,图形越平坦。
通常,如果样本的偏度接近于 0,且峰度接近于 3,则可以认为总体的分布接近于正态分布。
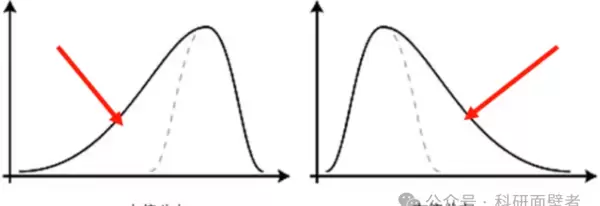
偏度:用于度量随机变量概率分布的不对称性。当偏度 < 0 时,概率分布图左偏;当偏度 = 0 时,表示数据相对均匀地分布在平均值两侧,但不一定是对称分布;当偏度 > 0 时,概率分布图右偏。
频数(频率)分布统计示例
以下为实验数据示例:
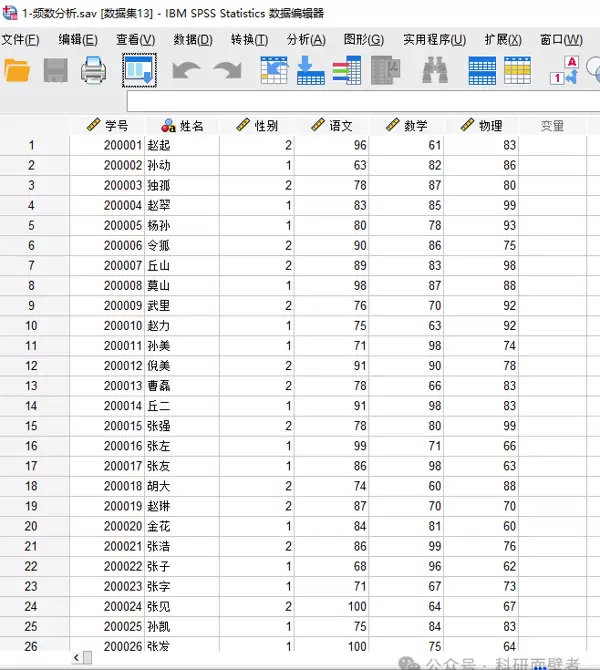
例如,对数学和语文成绩进行分析:
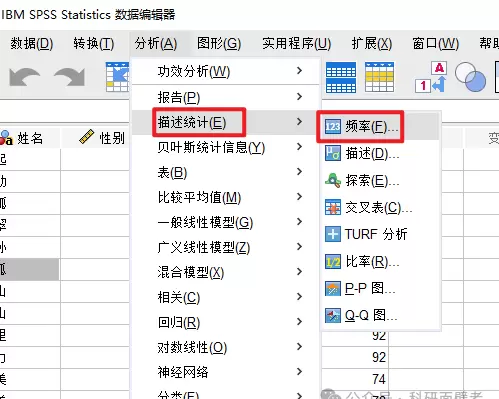
选择所需的统计量,如百分位值,查看特定百分比处的值,例如四分位数即 25%、50%、75% 处的值。也可以设置分割点,默认每 10 个分为一组,或者输入具体的百分位数。
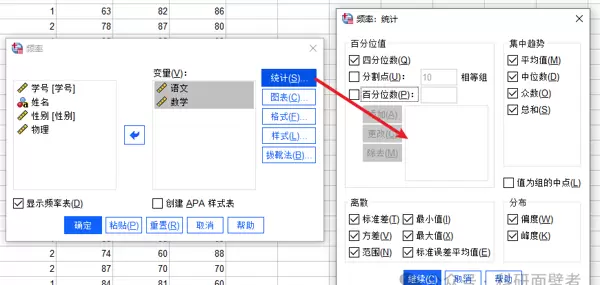
统计结果如下所示:
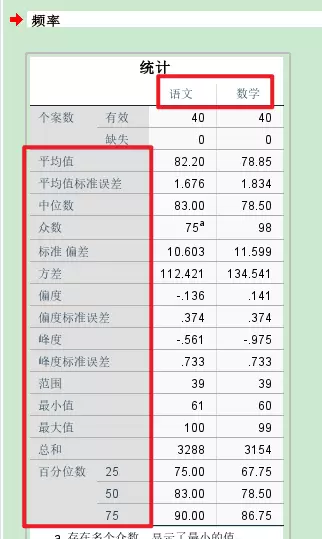
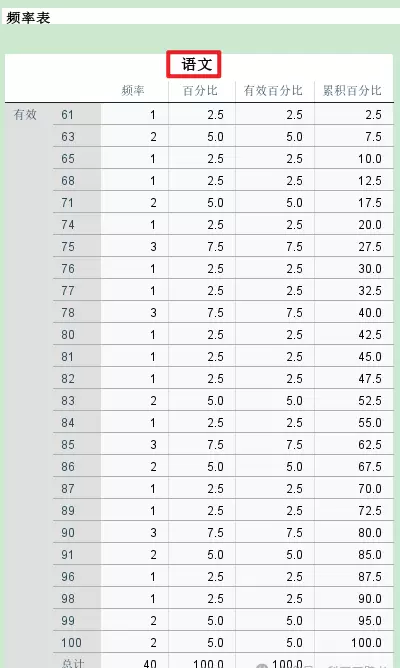
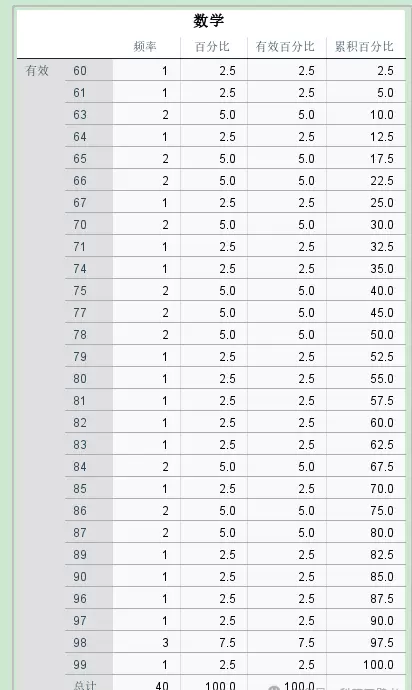
从统计结果中可以看到平均值、中位数、范围等统计值。如果选择了图表选项,还可以进一步生成直方图、饼图和条形图。以直方图为例:
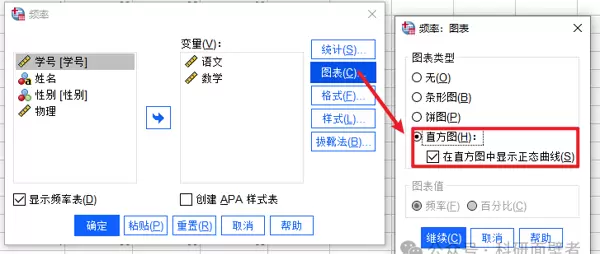
可以分别获得语文和数学成绩的频率分布直方图:
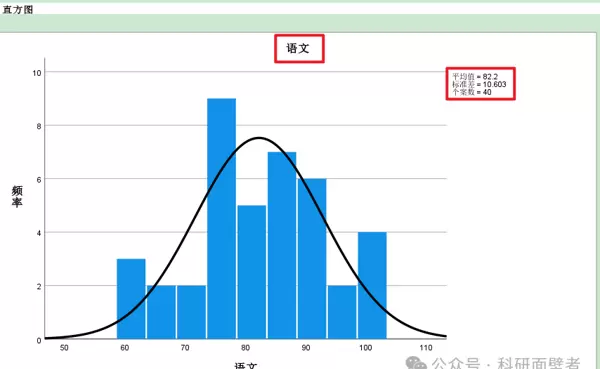
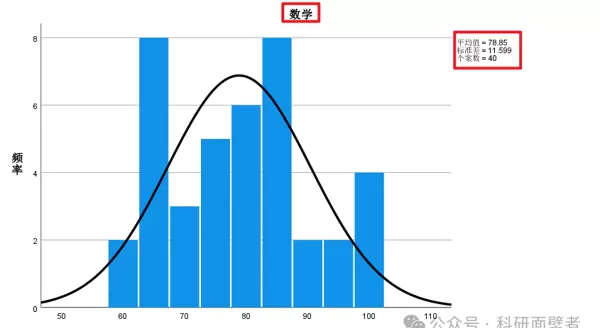
关于 SPSS 结果中的“峰度系数”为何会出现负数
这是因为 SPSS 中计算的是经过调整的峰度系数,即原始的峰度系数 kurtosis 减去常数 3 后的结果,称为超峰度系数 ek。因此,超峰度系数 ek 的取值范围可以包括负数。在 SPSS 中,描述统计默认计算的就是这个超峰度 ek。
判断准则为:正态分布 ek = 0;对于未知分布,当 ek < 0 时,表示分布较为扁平;当 ek > 0 时,表示分布较为尖锐。
SPSS 27 安装过程及更多免费教程和软件分析
更多关于 SPSS 27 的安装过程、免费教程和软件分析信息,请参考以下资源:




 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







