发帖
雷达卡
一、应用背景
非参数检验用于研究定类数据与定量数据之间的关系情况。例如研究人员想知道不同性别学生的购买意愿是否有显著差异。如果购买意愿呈现出正态性，则建议使用方差分析，如果购买意愿没有呈现出正态性特质，此时建议可使用非参数检验。此案例研究某车间用4种不同的操作方法做若干批试验，检验操作方法对产品的优等品率是否有显著影响。
二、SPSSAU操作
1.SPSSAU操作如下图：
2.将数据放入分析框中，SPSSAU系统对数据进行处理后，自动生成分析结果如下：
三、分析
结果解读以及计算公式：
1.Kruskal-Wallis检验统计量H 值
① 对于有结时，不校正的检验统计量为：
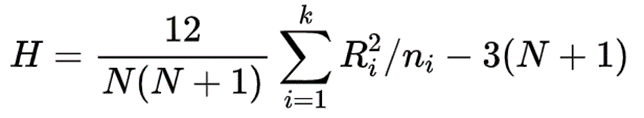
② 对于有结时，校正的检验统计量为
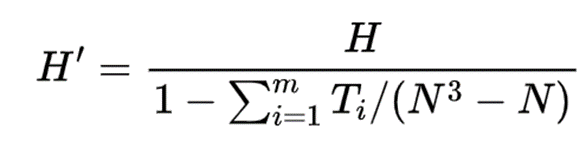
3.结论
从上表可以看出：ff超过两组组成，因而使用Kruskal-Wallis检验统计量进行分析。不同ff样本对于ydp1全部均呈现出显著性(p<0.05)，意味着不同ff样本对于ydp1均有着差异性。
四、扩展
1.SPSSAU分析建议：
MannWhitney U统计量：
式中， 表示Y的观测值大于X观测值的个数，
表示X的观测值大于Y观察值的个数。注意有
2.说明
（1）如果X的组别为两组，比如上表中男和女共两组，则应该使用MannWhitney统计量，如果组别超过两组，则应该使用Kruskal-Wallis统计量结果。SPSSAU自动为你选择MannWhitney或者Kruskal-Wallis统计量。
（2）如果p 值小于0.05，但是却出现中位数基本一致没有差异，原因在于数据分布不同所致，此时使用非参数检验将无实际现实意义。SPSSAU建议使用箱线图进行检查，并且建议最终使用方差分析进行差异检验。
（3）如果P小于0.05，但是中位数并没有明显的差异，说明差异来源于数据分布不同（而非中位数差异），可使用“箱线图”进行查看。
3.分类
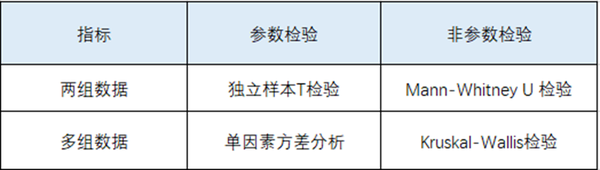
4.具体操作
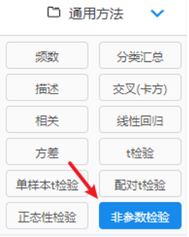
（1）点击SPSSAU通用方法里面的‘非参数检验’按钮。如下图：
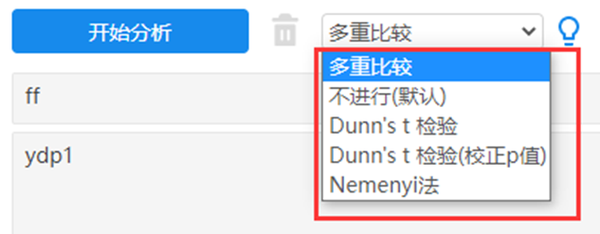
（2） 拖拽数据后开始分析：
五、参考文献
《SPSS统计分析（第五版）》
《SPSS统计分析基础教程（第2版）》
京公网安备 11010802022788号
