楼主: lenosky
2674 18

[经管数据集] A股公司违约概率风险数据stata代码do文件违约概率EDF结果1999-2021 [推广有奖]

已卖：8279份资源

大师

49%

还不是VIP/贵宾

-

0%
威望
0 级
论坛币
1914 个
通用积分
663.5734
学术水平
17 点
热心指数
47 点
信用等级
6 点
经验
30497 点
帖子
5598
精华
0
在线时间
14962 小时
注册时间
2010-12-14
最后登录
2025-12-5
楼主
lenosky 在职认证  发表于 2022-10-29 22:55:43 |AI写论文

+2 论坛币
k人 参与回答

经管之家送您一份

应届毕业生专属福利!

求职就业群
赵安豆老师微信：zhaoandou666

经管之家联合CDA

送您一个全额奖学金名额~ !

立即领取

感谢您参与论坛问题回答

经管之家送您两个论坛币！

+2 论坛币
A股公司违约概率风险数据stata代码do文件违约概率EDF结果1999-2021
采用Bharath和Shumway（2008）提出的Naive模型估计违约概率（EDF）作为违约风险的代理变量，具体如式（1）：

式（1）中
DDit表示违约距离
Equityit表示公司总市值，为股票发行总数与年末市场价格的乘积
Debtit是公司债务的面值，是公司年末短期负债与年末长期负债的二分之一的加总
rit-1是企业滞后一年的年度收益率
Tit在公式中被设置为1年
σVit是公司资产波动率的估计量，通过σEit（股票收益率的波动率）计算得出。
σEit是股票收益率的波动率，利用公司上一年度的月度收益率数据取标准差求得。

σVit的计算如式(2):


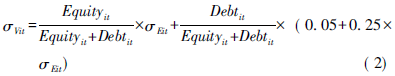
在式(1)、(2)的基础上，计算出违约风险距离DDit，然后通过标准累计正态分布函数Normal（.）求出企业违约概率，如式(3)：

企业债务违约风险指标（EDF)取值范围在0至1之间，其值越大，代表企业的违约风险越高。

同时，参考孙铮等(2006)、许红梅和李春涛(2020)的做法用事后债务违约概率来进行稳健性检验，即以企业上年度短期借款(包括一年内到期的长期借款) 与当期偿还借款额度(对应现金流量表中“偿还债务所支付的现金”) 的差额来衡量公司是否按期偿还了借款。我们设置虚拟变量VIOLATE表示企业事后违约概率。当该差额大于0时，表示企业没有按期偿还借款，变量VIOLATE取1，表示企业违约；否则取0，表示企业没有违约。

数据说明
样本选择：全部A股1999-2021
行业参照证监会2012年行业分类标准，已剔除金融行业和st公司

参考文献
许红梅,李春涛.劳动保护、社保压力与企业违约风险——基于《社会保险法》实施的研究[J].金融研究

附件预览
搜狗截图22年10月29日2256_3.png

计算结果图片：
搜狗截图22年10月29日2251_1.png
样本量：
搜狗截图22年10月29日2251_2.png
违约概率风险2021.rar (38.37 MB, 需要: RMB 65535 元) 本附件包括：
  • 劳动保护、社保压力与企业违约风险_基于社会保险法实施的研究.pdf
  • 计算do文件.do
  • 非金融非ST公司的违约风险计算结果.xlsx
  • 非金融非ST公司的违约风险计算结果.dta
  • Sigma_E.dta
  • 月个股回报率.dta
  • 上市公司数据汇总.xlsx
  • 上市公司数据汇总.dta
 违约概率风险2021new.rar (90.22 MB, 需要: RMB 38 元) 本附件包括：
  • 月个股回报率.dta
  • 劳动保护、社保压力与企业违约风险_基于社会保险法实施的研究.pdf
  • 计算do文件.do
  • 非金融非ST公司的违约风险计算结果.xlsx
  • 非金融非ST公司的违约风险计算结果.dta
  • TRD_Year.xlsx
  • TRD_Year.dta
  • TRD_Co.xlsx
  • TRD_Co.dta
  • Sigma_E.dta
  • r.dta
  • FS_Comscfd.xlsx
  • FS_Comscfd.dta
  • CSR_Finidx.xlsx
  • CSR_Finidx.dta






二维码

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

分享0
关键词：Stata 违约概率 tata do文件 A股公司

搜狗截图22年10月29日2256_3.png (10.66 KB)

搜狗截图22年10月29日2256_3.png

相关帖子

沙发
lucycya(真实交易用户) 发表于 2023-1-10 11:53:20
你好，我买了数据，但数据的均值接近50%，与已有文献的2%差距比较大，能否帮忙检查一下
藤椅
lenosky(未真实交易用户) 在职认证  发表于 2023-1-10 13:37:48 来自手机
lucycya 发表于 2023-1-10 11:53
你好，我买了数据，但数据的均值接近50%，与已有文献的2%差距比较大，能否帮忙检查一下
我晚上看下后发你最新的
板凳
lenosky(未真实交易用户) 在职认证  发表于 2023-1-10 21:01:15
请下载  违约概率风险2021new.rar 这个最新附件。
报纸
lenosky(未真实交易用户) 在职认证  发表于 2023-2-25 21:43:45
A股上市公司企业范霍恩和希金斯可持续发展能力数据2021-2000  可持续增长率https://bbs.pinggu.org/thread-11347299-1-1.html
平安银行启动零售业务的架构调整进行数字化转型事件研究数据和图表https://bbs.pinggu.org/thread-11346223-1-1.html
上市A股其他高管任职信息数据2010-2021https://bbs.pinggu.org/thread-11346197-1-1.html
沪深a股董事长与总经理任职数据2000-2021https://bbs.pinggu.org/thread-11346193-1-1.html
蓝帆医疗2018.1.8事件研究超额收益率、累计超额收益率数据与图表https://bbs.pinggu.org/thread-11344281-1-1.html
紫金矿业2021.12.15事件研究超额收益率、累计超额收益率数据与图表https://bbs.pinggu.org/thread-11340330-1-1.html
A股上市公司避税活动、企业避税数据构建do代码与计算结果2021-1998年https://bbs.pinggu.org/thread-11336679-1-1.html
智飞生物2022.2.7事件研究超额收益率、累计超额收益率数据与图表https://bbs.pinggu.org/thread-11335667-1-1.html
A股上市公司企业声誉指标及相关数据2000-2021年https://bbs.pinggu.org/thread-11335659-1-1.html
A股上市企业有效价差和相对有效价差数据2022-2001https://bbs.pinggu.org/thread-11334015-1-1.html
创业板指数399006收益率  收盘价2010/6/1-2023/1/20https://bbs.pinggu.org/thread-11332357-1-1.html
CAPM资本资产定价模型与商品期货研究数据https://bbs.pinggu.org/thread-11329428-1-1.html
中小企业板A股公司数字普惠研究论文面板数据2011-2020年https://bbs.pinggu.org/thread-11329284-1-1.html
A股上市企业信息不对称指数ASY数据与stata代码2022-2007https://bbs.pinggu.org/thread-11326583-1-1.html
A股非控股大股东数量统计2008-2021https://bbs.pinggu.org/thread-11326380-1-1.html
上市公司会务费+差旅费+招待费数据2010-2020https://bbs.pinggu.org/thread-11326307-1-1.html
上市公司社会信任数据https://bbs.pinggu.org/thread-11320131-1-1.html
2008-2020全国农村一二三产业融合综合评价指标数据https://bbs.pinggu.org/thread-11320054-1-1.html
全国各省份对外开放程度 对外开放水平  对外贸易度数据1993-2021年https://bbs.pinggu.org/thread-11319160-1-1.html
全国各省居民人均可支配收入数据1998-2021年https://bbs.pinggu.org/thread-11318822-1-1.html
A股是否四大审计 分析师关注数量  研报关注数量 信息披露考评2001-2021https://bbs.pinggu.org/thread-11318655-1-1.html
机构投资者持股数据2000-2021https://bbs.pinggu.org/thread-11318417-1-1.html
沪深交易所公司融资融券数据2022-2000https://bbs.pinggu.org/thread-11318402-1-1.html
A股上市公司环保处罚数据汇总2009-2022年https://bbs.pinggu.org/thread-11318390-1-1.html
全国商业银行数字化转型指数2021-2010  年https://bbs.pinggu.org/thread-11317861-1-1.html
A股上市公司国际化程度2021-2008年https://bbs.pinggu.org/thread-11317868-1-1.html
上市公司共同富裕公益慈善关键数据2011-2021https://bbs.pinggu.org/thread-11313308-1-1.html
上市公司共同富裕顾客共享关键数据2011-2021https://bbs.pinggu.org/thread-11313307-1-1.html
共同富裕良性竞争关键数据2011-2021年https://bbs.pinggu.org/thread-11313305-1-1.html
共同富裕其他合作伙伴共享关键数据2011-2021https://bbs.pinggu.org/thread-11313304-1-1.html
共同富裕员工就业关键数据2011-2021https://bbs.pinggu.org/thread-11313301-1-1.html
【最新含do文件】沪深交易所SYN股价同步性与股价信息含量数据1996-2022年https://bbs.pinggu.org/thread-11313206-1-1.html
中国城市县域经度纬度数据最新https://bbs.pinggu.org/thread-11312551-1-1.html
【最新含do文件】信息披露质量KV指数数据1998-2022年https://bbs.pinggu.org/thread-11310672-1-1.html
沪深A股流动性指标Gamma数据2022-2000年https://bbs.pinggu.org/thread-11310395-1-1.html
A股女性高管平均任期面板数据2015-2021年https://bbs.pinggu.org/thread-11310157-1-1.html
A股年度换手率、月均换手率、月均超额换手率数据1990-2022年https://bbs.pinggu.org/thread-11309205-1-1.html
高管平均年龄与男性比例女性比例2015-2021  +女性受教育程度https://bbs.pinggu.org/thread-11303668-1-1.html
全国31省市金融监管指标数据最全版无缺失值2007-2021年https://bbs.pinggu.org/thread-11303070-1-1.html
沪深A股公司WACC加权平均资本成本数据2021-2006  面板格式https://bbs.pinggu.org/thread-11303069-1-1.html
上市企业期末股权质押冻结汇总2019-2021https://bbs.pinggu.org/thread-11300885-1-1.html
沪深上市企业对赌协议数据汇总2014-2022https://bbs.pinggu.org/thread-11300883-1-1.html
全国各省市并购数量和并购总额统计数据2000-2021年https://bbs.pinggu.org/thread-11300878-1-1.html
西宁特钢事件研究数据与数据制图https://bbs.pinggu.org/thread-11300236-1-1.html
A股上市公司对赌协议数据汇总2007-2022.12.20https://bbs.pinggu.org/thread-11298935-1-1.html
高管风险偏好do代码和计算数据1998-2021年https://bbs.pinggu.org/thread-11298855-1-1.html
英国申请失业金人数、失业救济率、新增申请失业金人数、失业率1971-2022.10https://bbs.pinggu.org/thread-11298249-1-1.html
英国流通中的现金 M1 M2  M3月度数据1970-2022.9https://bbs.pinggu.org/thread-11298248-1-1.html
英国进出口数据  商品贸易服务贸易数据1997-2022.11月度数据https://bbs.pinggu.org/thread-11298244-1-1.html
英国基准利率数据1975-2022.11每日数据https://bbs.pinggu.org/thread-11298240-1-1.html
NYMEX  WTI原油价格数据1988-2022-11每日数据https://bbs.pinggu.org/thread-11298238-1-1.html
stata winsor2命令下载https://bbs.pinggu.org/thread-11298223-1-1.html
本科生毕业论文常用上市公司数据变量大全1990-2021年https://bbs.pinggu.org/thread-11297749-1-1.html
上市公司获得申请的绿色专利数量1992-2021https://bbs.pinggu.org/thread-11297525-1-1.html
上市公司员工薪酬关键指标数据2011-2021https://bbs.pinggu.org/thread-11292973-1-1.html
上市公司绿色专利申请总量和绿色专利获得总量数据1991-2021年https://bbs.pinggu.org/thread-11291691-1-1.html
上市公司共同富裕评级统计数据2011-2021年https://bbs.pinggu.org/thread-11289862-1-1.html
上市公司共同富裕员工保障关键数据2011-2021https://bbs.pinggu.org/thread-11289846-1-1.html
上市公司股东共享关键数据2011-2021年https://bbs.pinggu.org/thread-11289827-1-1.html
上市公司共同富裕税收贡献关键指标数据2011-2021https://bbs.pinggu.org/thread-11289638-1-1.html
A股公司融资约束ww指数数据和do代码过程1998-2021https://bbs.pinggu.org/thread-11288424-1-1.html
中国上市商业银行竞争程度数据和do计算代码2009-2021年——勒纳指数Lernerhttps://bbs.pinggu.org/thread-11282444-1-1.html
英国制造业PMI 服务业PMI  英国GFK消费者信心指数月度数据2002-2022.9https://bbs.pinggu.org/thread-11281289-1-1.html
英国国债收益率数据1994-2022.10https://bbs.pinggu.org/thread-11281287-1-1.html
中国数字经济创新创业指数2010-2020  中国区域创新创业指数1990-2020https://bbs.pinggu.org/thread-11281227-1-1.html
上市公司数字创新论文数量统计数据2010-2021https://bbs.pinggu.org/thread-11280507-1-1.html
上市公司环境支撑评分数据2021-2011https://bbs.pinggu.org/thread-11280501-1-1.html
上市公司数字化应用评分数据11-21年https://bbs.pinggu.org/thread-11280498-1-1.html
上市企业数字化转型指数2011-2021https://bbs.pinggu.org/thread-11280485-1-1.html
上市公司监管函信息数据2002-05-16  至 2022-12-09https://bbs.pinggu.org/thread-11280482-1-1.html
沪深交易所上市企业总经理数据整理2005-2021年https://bbs.pinggu.org/thread-11280043-1-1.html
上市公司增值税实际税负数据2003-2021年https://bbs.pinggu.org/thread-11279269-1-1.html
A股上市企业风险经营RISK数据和stata代码构建过程1995-2021最优版https://bbs.pinggu.org/thread-11278069-1-1.html
A股公司企业风险承担标准差和极差3年口径数据和stata代码年份优化版1994-2021https://bbs.pinggu.org/thread-11276797-1-1.html
非st非金融行业A股公司管理层权力数据与stata代码2006-2021https://bbs.pinggu.org/thread-11274263-1-1.html
地板
lenosky(未真实交易用户) 在职认证  发表于 2023-2-25 21:45:56
A股上市公司企业范霍恩和希金斯可持续发展能力数据2021-2000  可持续增长率https://bbs.pinggu.org/thread-11347299-1-1.html
平安银行启动零售业务的架构调整进行数字化转型事件研究数据和图表https://bbs.pinggu.org/thread-11346223-1-1.html
上市A股其他高管任职信息数据2010-2021https://bbs.pinggu.org/thread-11346197-1-1.html
沪深a股董事长与总经理任职数据2000-2021https://bbs.pinggu.org/thread-11346193-1-1.html
蓝帆医疗2018.1.8事件研究超额收益率、累计超额收益率数据与图表https://bbs.pinggu.org/thread-11344281-1-1.html
紫金矿业2021.12.15事件研究超额收益率、累计超额收益率数据与图表https://bbs.pinggu.org/thread-11340330-1-1.html
A股上市公司避税活动、企业避税数据构建do代码与计算结果2021-1998年https://bbs.pinggu.org/thread-11336679-1-1.html
智飞生物2022.2.7事件研究超额收益率、累计超额收益率数据与图表https://bbs.pinggu.org/thread-11335667-1-1.html
A股上市公司企业声誉指标及相关数据2000-2021年https://bbs.pinggu.org/thread-11335659-1-1.html
A股上市企业有效价差和相对有效价差数据2022-2001https://bbs.pinggu.org/thread-11334015-1-1.html
创业板指数399006收益率  收盘价2010/6/1-2023/1/20https://bbs.pinggu.org/thread-11332357-1-1.html
CAPM资本资产定价模型与商品期货研究数据https://bbs.pinggu.org/thread-11329428-1-1.html
中小企业板A股公司数字普惠研究论文面板数据2011-2020年https://bbs.pinggu.org/thread-11329284-1-1.html
A股上市企业信息不对称指数ASY数据与stata代码2022-2007https://bbs.pinggu.org/thread-11326583-1-1.html
A股非控股大股东数量统计2008-2021https://bbs.pinggu.org/thread-11326380-1-1.html
上市公司会务费+差旅费+招待费数据2010-2020https://bbs.pinggu.org/thread-11326307-1-1.html
上市公司社会信任数据https://bbs.pinggu.org/thread-11320131-1-1.html
2008-2020全国农村一二三产业融合综合评价指标数据https://bbs.pinggu.org/thread-11320054-1-1.html
全国各省份对外开放程度 对外开放水平  对外贸易度数据1993-2021年https://bbs.pinggu.org/thread-11319160-1-1.html
全国各省居民人均可支配收入数据1998-2021年https://bbs.pinggu.org/thread-11318822-1-1.html
A股是否四大审计 分析师关注数量  研报关注数量 信息披露考评2001-2021https://bbs.pinggu.org/thread-11318655-1-1.html
机构投资者持股数据2000-2021https://bbs.pinggu.org/thread-11318417-1-1.html
沪深交易所公司融资融券数据2022-2000https://bbs.pinggu.org/thread-11318402-1-1.html
A股上市公司环保处罚数据汇总2009-2022年https://bbs.pinggu.org/thread-11318390-1-1.html
全国商业银行数字化转型指数2021-2010  年https://bbs.pinggu.org/thread-11317861-1-1.html
A股上市公司国际化程度2021-2008年https://bbs.pinggu.org/thread-11317868-1-1.html
上市公司共同富裕公益慈善关键数据2011-2021https://bbs.pinggu.org/thread-11313308-1-1.html
上市公司共同富裕顾客共享关键数据2011-2021https://bbs.pinggu.org/thread-11313307-1-1.html
共同富裕良性竞争关键数据2011-2021年https://bbs.pinggu.org/thread-11313305-1-1.html
共同富裕其他合作伙伴共享关键数据2011-2021https://bbs.pinggu.org/thread-11313304-1-1.html
共同富裕员工就业关键数据2011-2021https://bbs.pinggu.org/thread-11313301-1-1.html
【最新含do文件】沪深交易所SYN股价同步性与股价信息含量数据1996-2022年https://bbs.pinggu.org/thread-11313206-1-1.html
中国城市县域经度纬度数据最新https://bbs.pinggu.org/thread-11312551-1-1.html
【最新含do文件】信息披露质量KV指数数据1998-2022年https://bbs.pinggu.org/thread-11310672-1-1.html
沪深A股流动性指标Gamma数据2022-2000年https://bbs.pinggu.org/thread-11310395-1-1.html
A股女性高管平均任期面板数据2015-2021年https://bbs.pinggu.org/thread-11310157-1-1.html
A股年度换手率、月均换手率、月均超额换手率数据1990-2022年https://bbs.pinggu.org/thread-11309205-1-1.html
高管平均年龄与男性比例女性比例2015-2021  +女性受教育程度https://bbs.pinggu.org/thread-11303668-1-1.html
全国31省市金融监管指标数据最全版无缺失值2007-2021年https://bbs.pinggu.org/thread-11303070-1-1.html
沪深A股公司WACC加权平均资本成本数据2021-2006  面板格式https://bbs.pinggu.org/thread-11303069-1-1.html
上市企业期末股权质押冻结汇总2019-2021https://bbs.pinggu.org/thread-11300885-1-1.html
沪深上市企业对赌协议数据汇总2014-2022https://bbs.pinggu.org/thread-11300883-1-1.html
全国各省市并购数量和并购总额统计数据2000-2021年https://bbs.pinggu.org/thread-11300878-1-1.html
西宁特钢事件研究数据与数据制图https://bbs.pinggu.org/thread-11300236-1-1.html
A股上市公司对赌协议数据汇总2007-2022.12.20https://bbs.pinggu.org/thread-11298935-1-1.html
高管风险偏好do代码和计算数据1998-2021年https://bbs.pinggu.org/thread-11298855-1-1.html
英国申请失业金人数、失业救济率、新增申请失业金人数、失业率1971-2022.10https://bbs.pinggu.org/thread-11298249-1-1.html
英国流通中的现金 M1 M2  M3月度数据1970-2022.9https://bbs.pinggu.org/thread-11298248-1-1.html
英国进出口数据  商品贸易服务贸易数据1997-2022.11月度数据https://bbs.pinggu.org/thread-11298244-1-1.html
英国基准利率数据1975-2022.11每日数据https://bbs.pinggu.org/thread-11298240-1-1.html
NYMEX  WTI原油价格数据1988-2022-11每日数据https://bbs.pinggu.org/thread-11298238-1-1.html
stata winsor2命令下载https://bbs.pinggu.org/thread-11298223-1-1.html
本科生毕业论文常用上市公司数据变量大全1990-2021年https://bbs.pinggu.org/thread-11297749-1-1.html
上市公司获得申请的绿色专利数量1992-2021https://bbs.pinggu.org/thread-11297525-1-1.html
上市公司员工薪酬关键指标数据2011-2021https://bbs.pinggu.org/thread-11292973-1-1.html
上市公司绿色专利申请总量和绿色专利获得总量数据1991-2021年https://bbs.pinggu.org/thread-11291691-1-1.html
上市公司共同富裕评级统计数据2011-2021年https://bbs.pinggu.org/thread-11289862-1-1.html
上市公司共同富裕员工保障关键数据2011-2021https://bbs.pinggu.org/thread-11289846-1-1.html
上市公司股东共享关键数据2011-2021年https://bbs.pinggu.org/thread-11289827-1-1.html
上市公司共同富裕税收贡献关键指标数据2011-2021https://bbs.pinggu.org/thread-11289638-1-1.html
A股公司融资约束ww指数数据和do代码过程1998-2021https://bbs.pinggu.org/thread-11288424-1-1.html
中国上市商业银行竞争程度数据和do计算代码2009-2021年——勒纳指数Lernerhttps://bbs.pinggu.org/thread-11282444-1-1.html
英国制造业PMI 服务业PMI  英国GFK消费者信心指数月度数据2002-2022.9https://bbs.pinggu.org/thread-11281289-1-1.html
英国国债收益率数据1994-2022.10https://bbs.pinggu.org/thread-11281287-1-1.html
中国数字经济创新创业指数2010-2020  中国区域创新创业指数1990-2020https://bbs.pinggu.org/thread-11281227-1-1.html
上市公司数字创新论文数量统计数据2010-2021https://bbs.pinggu.org/thread-11280507-1-1.html
上市公司环境支撑评分数据2021-2011https://bbs.pinggu.org/thread-11280501-1-1.html
上市公司数字化应用评分数据11-21年https://bbs.pinggu.org/thread-11280498-1-1.html
上市企业数字化转型指数2011-2021https://bbs.pinggu.org/thread-11280485-1-1.html
上市公司监管函信息数据2002-05-16  至 2022-12-09https://bbs.pinggu.org/thread-11280482-1-1.html
沪深交易所上市企业总经理数据整理2005-2021年https://bbs.pinggu.org/thread-11280043-1-1.html
上市公司增值税实际税负数据2003-2021年https://bbs.pinggu.org/thread-11279269-1-1.html
A股上市企业风险经营RISK数据和stata代码构建过程1995-2021最优版https://bbs.pinggu.org/thread-11278069-1-1.html
A股公司企业风险承担标准差和极差3年口径数据和stata代码年份优化版1994-2021https://bbs.pinggu.org/thread-11276797-1-1.html
非st非金融行业A股公司管理层权力数据与stata代码2006-2021https://bbs.pinggu.org/thread-11274263-1-1.html
7楼
Eveline1223(真实交易用户) 发表于 2023-2-26 17:09:49 来自手机
lenosky 发表于 2022-10-29 22:55
A股公司违约概率风险数据stata代码do文件违约概率EDF结果1999-2021
采用Bharath和Shumway（2008）提出的Na ...
买了2021new.rar的压缩包，也下载失败了
8楼
lenosky(未真实交易用户) 在职认证  发表于 2023-2-26 20:28:46 来自手机
Eveline1223 发表于 2023-2-26 17:09
买了2021new.rar的压缩包，也下载失败了
怎么失败呢，x私信我
9楼
zhangshu1234(未真实交易用户) 发表于 2023-3-25 09:10:16
lucycya 发表于 2023-1-10 11:53
你好，我买了数据，但数据的均值接近50%，与已有文献的2%差距比较大，能否帮忙检查一下
你好 能问问现在的EDF均值合适了吗？
10楼
lenosky(未真实交易用户) 在职认证  发表于 2023-3-25 10:51:11
zhangshu1234 发表于 2023-3-25 09:10
你好 能问问现在的EDF均值合适了吗？
合适了，请下载new这个附件。
返回列表
12下一页
高级模式
B Color Image Link Quote Code Smilies
您需要登录后才可以回帖 登录 | 我要注册

本版微信群
jg-xs1
拉您进交流群

京ICP备16021002号-2 京B2-20170662号 京公网安备 11010802022788号 论坛法律顾问：王进律师 知识产权保护声明   免责及隐私声明

GMT+8, 2025-12-5 18:30