认识决策树
一·概念
决策树是一种以特征为节点、决策规则为分支、类别 / 结果为叶节点的树形结构监督学习模型。通过递归划分数据构建,它能够直观地实现分类与回归任务,因其逻辑简单、无需复杂的数据预处理而在数据分析和机器学习入门等领域广泛应用。
该模型的优势在于易于理解、不需要进行数据预处理且训练效率高,可以可视化解释;但缺点是容易过拟合,并对异常值敏感,通常需要通过剪枝来优化泛化能力。
二·属性划分
决策树学习的核心在于如何选择最优的划分属性。以下是三种主流的属性划分方法:
- 信息增益 → ID3 算法(核心特征选择指标,仅支持离散特征)
- 信息增益率 → C4.5 算法(改进的指标,解决了 ID3 偏好多取值特征的问题)
- 基尼系数 → CART 算法(分类任务专用,回归任务使用平方误差替代)
具体介绍
1. 信息增益(ID3 算法专属)
核心逻辑:基于信息熵(衡量混乱度),计算 “划分前总熵 - 划分后子集加权平均熵”,增益越大,纯度提升越明显;适用场景:仅离散型属性;优缺点:直观易懂,但偏好多取值特征(如身份证号这类无意义高维特征)。
2. 信息增益比(C4.5 算法专属)
核心逻辑:在信息增益的基础上引入 “属性固有值”(惩罚取值分散的特征),公式为 “信息增益 ÷ 属性固有值”;适用场景:离散型 + 连续型属性,支持缺失值处理;核心优势:解决了 ID3 的特征偏好问题,兼容性更强。
3. 基尼系数(CART 算法专属)
核心逻辑(分类任务):选择 “子集基尼系数加权和最小” 的属性;回归任务适配:用 “平方误差(MSE)” 替代,最小化子集数值离散程度;适用场景:所有属性类型,支持分类与回归双任务;核心优势:计算高效,是目前应用最广泛的划分方法。
Python 实现
这是实验所用到的数据
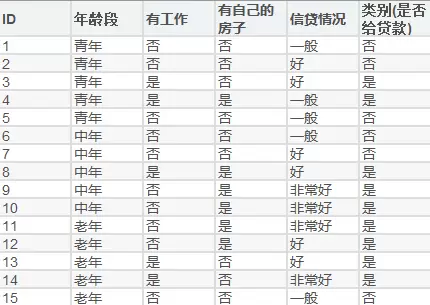
将其映射为数据形式后为:
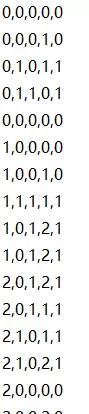
测试集:

熵的计算函数:
def calculate_entropy(y):
"""计算给定标签集合的熵"""
# 统计每个类别的样本数
counts = np.bincount(y)
# 计算每个类别的比例
probabilities = counts / len(y)
# 计算熵(忽略0概率,避免log(0)错误)
entropy = 0.0
for p in probabilities:
if p > 0:
entropy -= p * math.log2(p)
return entropy信息增益计算函数:
def calculate_information_gain(X, y, feature_idx):
"""计算指定特征的信息增益"""
# 1. 计算父节点的熵
parent_entropy = calculate_entropy(y)
# 2. 按特征取值拆分样本
feature_values = np.unique(X[:, feature_idx])
weighted_child_entropy = 0.0
for value in feature_values:
# 筛选该特征取值的样本
mask = (X[:, feature_idx] == value)
y_child = y[mask]
# 计算子节点的熵
child_entropy = calculate_entropy(y_child)
# 加权累加(权重为子节点样本数占比)
weighted_child_entropy += (len(y_child) / len(y)) * child_entropy
# 3. 信息增益 = 父节点熵 - 子节点加权熵
information_gain = parent_entropy - weighted_child_entropy
return information_gain增益率计算函数:
def calculate_information_gain_ratio(X, y, feature_idx):
"""计算指定特征的信息增益率"""
# 1. 计算信息增益
info_gain = calculate_information_gain(X, y, feature_idx)
# 2. 计算特征自身的熵(分裂信息)
feature_values = X[:, feature_idx]
split_info = calculate_entropy(feature_values) # 直接复用熵计算函数
# 3. 信息增益率 = 信息增益 / 分裂信息(避免除以0)
if split_info == 0:
return 0.0 # 若特征只有一个取值,增益率为0
return info_gain / split_info结果:

总结
决策树是一种直观且易于理解的监督学习方法,通过逐步划分特征形成树状结构来完成分类或回归任务。在贷款审批领域中,以信息增益和信息增益比为基础构建的决策树模型表现出色,均能实现测试集 100% 的准确率。提炼出的“有房直接批准、无房但有工作也能贷、无房且无工作者不予放款”的决策准则与业务逻辑相符。信息增益方法倾向于选取具有较高信息增益的属性(例如 “拥有房产”、“就业状况”),而信息增益比法则通过对高值特征施加惩罚以提高模型的泛化性能,两者在当前数据集上的表现趋于一致。决策树算法的优势在于其优秀的可解释性,所生成的规则符合行业常规认知,是实现贷款审批自动化的理想工具。此外,通过调整参数、扩展特征等手段,能够适应更为复杂的信贷环境,在“拟合度”与“泛化度”之间找到合适的平衡点,进一步增强其实用价值。




 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







