【原理到实战】实验异质性分析

是 否 +2 论坛币

k人 参与回答

经管之家送您一份

应届毕业生专属福利!

求职就业群

赵安豆老师微信：zhaoandou666

经管之家联合CDA

送您一个全额奖学金名额~ !

立即领取

感谢您参与论坛问题回答

经管之家送您两个论坛币！

+2 论坛币

什么是实验的异质性

1. 如何理解实验结果中的指标变化

当我们观察到如下试金石实验指标结果时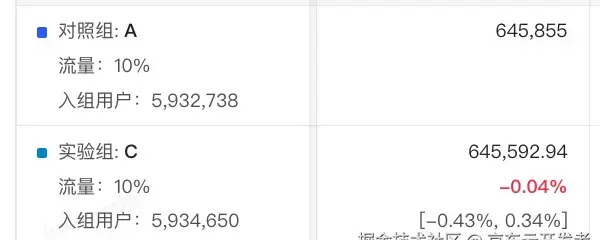 在进行解析之前，可能我们的第一反应是这样的 经过异质性分析后，可能会揭示实际情况是这样的

2. 概念解析与定义

实验的异质性通常称为HTE（即Heterogeneous Treatment Effects），意指实验中同一个治疗对不同的样本可能产生不同效果。此外，还有一些重要的概念需要了解：

英文简称	英文全称	中文译名	含义	公式
ATE	Average Treatment Effect	平均处理效应	所有实验对象的平均效果	ATE=E[Y(1)-Y(0)]
CATE	Conditional Average Treatment Effect	条件平均处理效应	满足特定条件的实验对象的平均效果	CATEX=E[Yx(1)-Yx(0) | x∈X]
ITE	Individual Treatment Effect	个体处理效应	某个实验对象的效果	ITEi=E[Yi(1)-Yi(0)], i=1,2,…N

** 此处采用Donald Rubin提出的潜在因果框架（Potencial outcome）来对实验效果进行统计公式上的描述 [1]* 由于行业内没有统一的定义，HTE、CATE、ITE概念在一定程度上会存在混用的情况，读者需要结合上下文综合理解这些名词的意义。

3. 异质性分析对于业务的意义

1. 了解策略对不同用户的不同效果，协助挖掘背后的业务逻辑，辅助迭代和进行新一轮的实验。
2. 尝试寻找策略最优子人群，让整体无效的策略有机会部分先行推广；反之亦然，减少部分负面策略的影响。
3. 对实验结果建模后预测，为线上提供动态的最优人群支持。

根据试金石测算，以某产品线下6月运行中的35个实验为例，仅23%左右的实验在实验人群视角未发现异质性。

异质性分析方法概述

1. 异质性分析的维度选择

对于分流单元的维度X，当X满足以下条件时，可以作为异质性的维度进行后续分析 ? T⊥X ，即 分析维度与实验分流无关（无混淆性） ?常见的简化方式：对于一个分流ID，选取他在首次进入实验前一天的标签值。

简单推导：

**T是随机化的， T⊥Y, T⊥X ，所以 E[Y_i(1) | x∈X] = E[Y_i(1) | T_i=1, x∈X] ，因此（3）成立。**

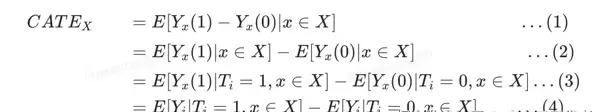
异质性分析的维度分析bad case举例

假设我们需要分析的实验策略为：根据用户的活跃度标签，低、中、高频用户的不同优惠券策略分别进行了新/老策略迭代。

分析目标 & 常见错误方法举例	不成立原因简述	推荐的实验分析方式
不同活跃度人群的策略效果 在实验运行7天后，利用实验用户在第7天的活跃度标签进行结果拆解。	在实验开始后，用户的活跃度标签受到了策略影响，即T⊥X不成立。	使用用户进入实验前1天的活跃度标签值分别分析低频、中频、高频策略对于相应用户的策略效果。
按天取每天用户的活跃度标签，对实验结果进行拆解。	用户的活跃度标签受到了策略影响，即T⊥X不成立。用户所在分组应该是固定的，不应随时间改变。	分别建立3个人群正交实验，分析高单价类目商品（如3C家电）和低单价类目商品（如休闲食品）的转化率差异。

2. 异质性分析的方法选择

研究对象	研究方法	适用场景	优缺点
CATE	维度下钻	低维，分析目标明确	+ 快速简单，便于理解 + 产品化容易 - 维度选择依赖分析师经验 - 交互效应处理困难
方差分析（ANOVA，ANCOVA）	低维，分析目标较明确，交互效应评估	+ 解释性强，统计学理论背书 + 可处理低维度交互效应 + 可作为特征选择的候选方法 - 基于线性模型假设 - 高维度交互效应解读困难
因果树（Causal Tree）	高维，分析目标不明确，希望探索	+ 模型符合分析直觉 - 复杂度不足，难以准确描述现实世界效果 - 为现代机器学习因果算法的基石之一，有更优替代方案
ITE	Meta-Learner	高维，希望输出ITE，算法训练	+ 适用于复杂场景 - 需要大量数据和计算资源

+ 算法常用于大规模并行计算，有工程化先例 + 在过去的模拟中X-learner对ITE估计的精确度表现优异 + X-learner通常使用xgboost模型，具备较强的数据特征处理能力 - 计算量大，耗费资源 - 需要调整参数 - 由于缺乏统计推断结果，通常不直接生成p-value，存在对ITE数值准确性的质疑，算法主要利用结果的排名

DML

• 高维
• 期望输出ITE和置信区间

+ 有严谨的统计理论证明了ITE估计的无偏有效性，可以生成样本级别的ITE及置信区间 + 在过去的模拟中Causal Forest DML对ITE估计的精确度表现优异 + DML模型框架本身具备一定的稳健性，在结合Forest模型后，调参需求低，不易过拟合，对各种特征有较强的处理能力 - 慢，耗资源，工程化先例少

ITE + CATE hybrid

ITE Model + Decision Tree Interpreter

• 高维
• 分析目标不明确，希望探索

+ 决策树的建模方法符合分析直觉 + ITE模型可以较好地对复杂的现实世界进行概括 - ITE模型可能会较慢

CATE、ITE建模方法的具体细节可参考附录

CATE下钻探索工具MVP版逻辑介绍

项目地址：
http://xingyun.jd.com/codingRoot/abtest_ds/CATE_model

模型逻辑：多维度的维度下钻 + Decision Tree Interpreter

快速开始：

from CATE_model.utils.workflow import CateWorkFlow
yaml_path = 'config.yaml'                # 按分析要求配置YAML文件
cate_workflow = CateWorkFlow(yaml_path)  # 初始化CATE对象
cate_workflow.prepare_analysis()         # 初始化ABTestAnalyzer
cate_workflow.execute_cate_auto()        # 自动执行所有环节
cate_workflow.df_out.styler              # 输出CATE差异最大子人群目标指标统计

项目基本流程

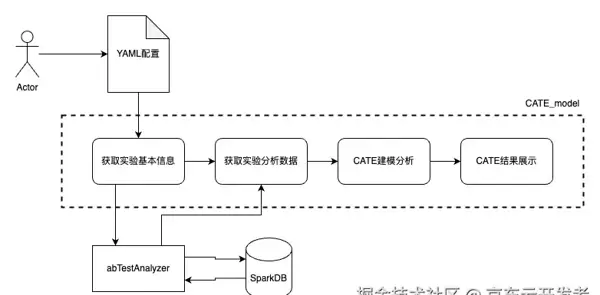
YAML配置方法：第一次可以先根据项目示例修改，并参考
YAML配置说明.md

项目MVP功能说明

1. 通过填写YAML配置，自动生成实验分析SQL并执行取数，目前包括
   • 自动获取试金石实验分流信息
   • 自动获取试金石实验指标信息
   • 解析实验CATE研究使用的用户标签表
   • 自动生成所有数据源的关联关系
2. 为实验CATE研究提供自动化工具，目前包括
   • 自动识别能最大化实验目标指标差异的子人群
   • 提供调参接口，高级用户可自定义模型参数
   • 提供可视化的模型结果输出，高级用户可根据输出调整模型表现
3. 为实验的下钻分析提供探索、分析功能，目前包括
   • CATE人群的实验效果统计检验
   • CATE人群的多指标拆解
   • CATE人群的特征描述

实验异质性分析案例
针对近期某频道重点改版实验，整体实验指标为负向且不显著，但通过运行分析工具后发现，有两类子人群分别具有正向和负向的显著效果

实验HTE人群统计

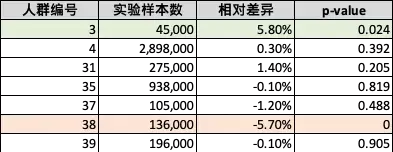
对于这些子人群，我们发现在业务漏斗上的变化各不相同，因此在下次对频道进行迭代时，产品经理可以根据分析结果有针对性地选择优化方向

人群编号 用户画像总结 频道uv 点击uv 加车uv 转化订单数
3 年轻人，低活跃度 1.0% 2.2% 2.6% 5.8%
38 非年轻人，高线城市用户，plus会员 -2.2% -2.2% -3.1% -5.7%

未来展望

1. 自定义分流表
2. 自定义画像表 & 经海路画像表
3. CATE模型迭代
4. 通用维度配置模版 & 业务场景模版
5. 图形化交互界面，简化输入配置

附录及参考资料

【1】

因果分析框架 & Donald Rubin的Potential Outcome
? Potential Outcome
? 设 TiTi 代表第i个样本是否接受了处理（treatment，策略影响），是为1，否为0
? YiYi 代表个体i的结果，另外记 {Yi(1),Yi(0)}{Yi?(1),Yi?(0)} 为个体i接受处理、对照的潜在结果
? 每个个体通常只会有1个状态，个体因果作用无法直接观察，我们只有 Yi=Ti?Yi(1)+(1?Ti)?Yi(0)Yi?=Ti??Yi?(1)+(1?Ti?)?Yi?(0)
? 在随机化实验的场景下，我们可以得到

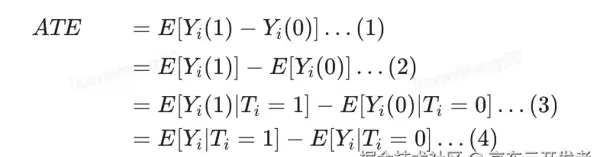
其中最重要的逻辑是：
T是随机化的， T⊥YT⊥Y ，所以 E[Yi(1)]=E[Yi(1)｜Ti=1]E[Yi?(1)]=E[Yi?(1)｜Ti?=1] ，因此（3）成立

因果推断（一）：两大因果推断框架及因果效应：
https://zhuanlan.zhihu.com/p/652174282
因果推断简介之二：Rubin Causal Model (RCM) 和随机化试验：
https://cosx.org/2012/03/causality2-rcm/

【2】 ANOVA与CATE的交互效应分析
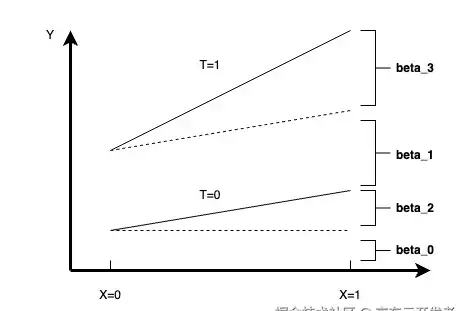
当需要进行异质性分析的维度为X时，我们可以通过构建下列回归方程来描述X在实验中是否存在显著的异质性，当 β3β3 对应的F-test显著时，我们就可以认为实验在维度X上存在显著的异质性

Y=β0+β1·T+β2·X+β3·X·TY=β0·+β1··T+β2··X+β3··X·T

当 X∈{0,1} 时，我们可以用下图来进行异质性的理解

CATE & ITE估计

思路1：对于每个参与实验的对象i，如果能获得 Yi(1) 和 Yi(0) 的合理预测，那么ITE就可以计算了。

思路2：对于实验群体X，如果能找到一种观测方法，求得 E[Yx(1)Yx(0)∣x∈X] ，那么CATE就可确定了。

Meta Learner的极简介绍

• S-Learner
  • 阶段1: 利用模型预测 μ(x,t)=E[Y∣X=x,T=t]
  • 阶段2: 定义CATE结果如下 τ(x)=μ(x,T=1)μ(x,T=0)
• T-Learner
  • ...

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

分享0 收藏0 回帖

关键词：质性分析 异质性 conditional Individual treatment