C++中STL用法 学习笔记

是 否 +2 论坛币

k人 参与回答

经管之家送您一份

应届毕业生专属福利!

求职就业群

赵安豆老师微信：zhaoandou666

经管之家联合CDA

送您一个全额奖学金名额~ !

立即领取

感谢您参与论坛问题回答

经管之家送您两个论坛币！

+2 论坛币

来源b站UP主ChrisKim_ZHT的解析

一、向量vector---#include<vector>

1.1 常见操作

• 创建

  vector<int> vet;//长度为0，无内容。
  	vector<int> vet1(100,1);//第一个为长度，第二个为每个元素初值。
  	vector<vector<int>> dp(5/*行数*/,vector<int>(6,1)/*列数（长度，初值）*/);//二维数组  
  	vector<vector<vector<int>>> dp2(5,vector<vector<int>> (6,vector<int> (4,1))) ;//三维数组

• 追加

  vector<int> arr;
  	arr.push_back(1);
  	arr.push_back(2);
  	for(auto &ele:arr)
  		cout<<ele<<endl;

• 移除末尾

  //尾删
  	arr.pop_back(); 
  	for(auto &ele:arr)
  		cout<<ele<<endl;

• 获取尺寸

  cout<<arr.size()<<endl;

• 清除全部

  ?arr.clear();

• 检查是否为空

  cout<<arr.empty()<<endl;//yes,return ture(1);no,return false(0).

• 调整尺寸

  ?arr.resize(5,3);//第一个为修改长度，第二个是初值

1.2 应用场合

如果使用int mat[100010][100010];会浪费内存，可能导致MLE。

推荐使用vector<vector<int>> mat(m+10,vector<int> (n+10))

1.3 注意事项

预先设定尺寸

小心size_t溢出。.size();返回值类型为size_t，溢出将变为0。

二、栈stack---#include<stack>

2.1 创建

//构造
    stack<double> stk;
    stk.push(1.0);//进栈 
    stk.push(1.4);
    cout<<stk.top()<<endl;
    stk.pop();//出栈 
    cout<<stk.top()<<endl;
	cout<<stk.size()<<endl;//取大小 
	cout<<stk.empty()<<endl;//判断是否为空
	
	//也可以把vector当成栈使用
	vector<int> vct;
	vct.push_back(1.0);
	vct.push_back(1.4);
	cout<<vct.back()<<endl;

2.2 适用场景

无需考虑性能瓶颈，直接使用。vector也可作为栈使用

2.3 注意

不可访问内部元素

以下为错误示例

for(auto ele:stk)
cout<<stk<<endl;

三、队列queue

3.1 常见操作

queue<int> que;
//进队
que.push(1);
que.push(2);
que.push(3);
cout<<que.front()<<endl;//队首
cout<<que.back()<<endl;//队尾
//出队
que.pop()
//返回大小
que.size()
//是否为空
que.empty();

3.2 使用场景

无需考虑性能瓶颈

3.3 注意

与栈相同

四、优先队列priority_queue

4.1 常见操作

priority_queue<int，vector<int>,greater<int>> p_que//小顶堆
priority_queue<int> pque//大顶堆
p_que.push(1);
p_que.push(2);
p_que.push(3);
cout<<p_que.top()<<endl;//取最大值
p_que.pop();

4.2 适用场景

每次向队列插入不确定大小的元素或取出最大/最小元素，元素数量n，插入次数k

每次插入快速排序k * nlog n

优先队列维护k*log n

4.3 注意

仅顶部堆可读

所有元素不可修改

如需修改则可以

int x=p_que.top();
p_que.pop();
p_que.push(x+1);

五、集合

5.1 常见操作

set<int> se;
se.insert(1);//插入，且存在互异性
se.insert(1);
se.insert(2);

se.erase(2);//擦除

se.find()//查找
if(se.find(1)!=se.end())
cout<<"yes";

se.count(1)//查找存在几个

cout<<se.size();

se.clear();

cout<<se.empty();
//遍历
for(set<int>::iterator it = st.begin();it != st.end();++it)
cout<<*it<<endl;

for(auto &ele:st)
cout<<ele<<endl;

5.2 适用场景

元素去重{1,1,2,2,3,4}-->{1,2,3,4}

维持顺序{1,5,3,7,9}-->{1,3,5,7,9}

检查元素是否存在

bool vis[100]
vis[1]=ture;
当数组里的数为1e19，无法编译。
用set

set<int> st;
st.insert(1);
st.insert(2);
if(count(1))
cout<<"yes"<<endl;

5.3 注意

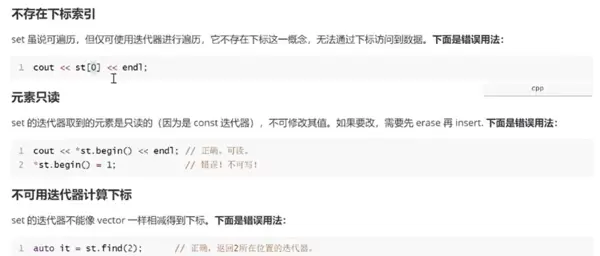
六、映射map---#include<map>

6.1 创建

map<int,int> mp;//从整型到整型的映射
mp[2]=1;
mp[2]=2;
cout<<mp[2];
if(mp.find(2)!=mp.end())
cout<<"yes"<<endl;

mp.erase();
cout<<mp.count(1);//出现次数
cout<<mp.size();
mp.clear;
cout<<mp.empty();


//遍历
mp[2]=1;
mp[1]=3;
mp[0]=5;
for(map<int,int>::iterator it=mp.begin();it!=mp.end();i++)
cout<<it->first<<" "<<it->second<<endl;

for(auto &pr:mp)
cout<<pr.first<<pr.second;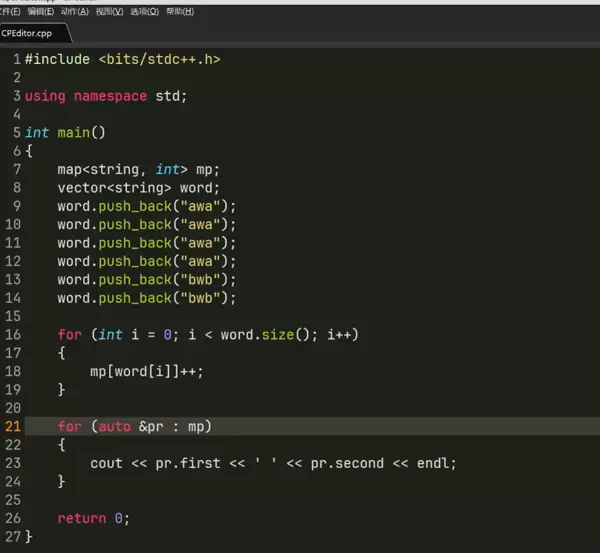

七、字符串String

7.1 常见操作

• 创建

  构造函数：

  string(长度, 初值)

  string s1;           // 构造字符串，为空
  string s2 = "awa!";  // 构造字符串，并赋值awa!
  string s3(10, '6');  // 构造字符串，通过构造函数构造为6666666666

• 输入输出

  C++

  string s;
  cin >> s;
  cout << s;

  C

  string s;
  char buf[100];
  scanf("%s", &buf);
  s = buf;
  printf("%s", s.c_str());

• 其他

  功能

  []

  s[1] = 'a';

  用途

  ==

  if (s1 == s2) ...

  字符串拼接

  +

  string s = s1 + s2;

  追加字符串

  +=

  s += "awa";

  提取子串

  .substr(起始下标, 子串长度)

  string sub = s.substr(2, 10);

  搜索字符串

  .find(字符串, 起始下标)

  int pos = s.find("awa");

  数值与字符串互转（C++11）

  源	目标	函数
  int / long long / float / double / long double	string	to_string()
  string	int	stoi()
  string	long long	stoll()
  string	float	stof()
  string	double	stod()
  string	long double	stold()

7.2 应用场景

非常实用！建议放弃字符数组，尽快采用string。

7.3 注意事项

追加字符串务必使用

+=

string 的 += 操作符，这将在原字符串上直接追加。而先 + 后 = 赋值，则会先创建一个临时变量，再复制给 string。

通常字符串长度可能非常长，使用 + 操作字符串容易导致TLE。

// 优化前: 15139ms
string s;
for (int i = 0; i < 5e5; i++)
    s = s + "a";

// 优化后: < 1ms (计时器显示0)
string s;
for (int i = 0; i < 5e5; i++)
    s += "a";

.substr()

方法的特殊参数 必须注意，C++ string 的提取子串的第一个参数是 子串起始索引 ，第二个参数是 子串长度 。 第二个参数不是子串结束点！不是子串结束点！需与 Java 等其他语言区分。

.find()

方法的复杂性 该方法实现为暴力匹配，时间复杂度为O(n²)。

八、二元组pair

#include <utility>

名副其实，用于存储二元组。

8.1 常见操作

• 创建

  pair<第一个值类型, 第二个值类型> pr

  第一种类型：要存储的第一个值的数据类型

  第二种类型：要存储的第二个值的数据类型

  pair<int, int> p1;
  pair<int, long long> p2;
  pair<char, int> p3;
  // ...

• 赋值

  传统方式

  pair<int, char> pr = make_pair(1, 'a');

  列表初始化 C++11

  pair<int, char> pr = {1, 'a'};

• 取值

  直接取值

  获取第一个值：

  .first

  获取第二个值：

  .second

  pair<int, char> pr = {1, 'a'};
  int awa = pr.first;
  char bwb = pr.second;

  结构化绑定 C++17

  pair<int, char> pr = {1, 'a'};
  auto &[awa, bwb] = pr;

• 比较

  直接使用

  ==

  运算符

  pair<int, int> p1 = {1, 2};
  pair<int, int> p2 = {1, 3};
  if (p1 == p2) { ... } // false

8.2 适用场景

任何需要二元组的情况都可使用，效率与自定义结构体相当。

8.3 注意事项

无

九、迭代器简介

3.1 迭代器是什么？

不谈抽象概念，直接看例子。

对于一个vector，我们可以使用下标遍历：

for (int i = 0; i < a.size(); i++)
    cout << a[i] << endl;

同时也可以使用迭代器遍历：

for (vector<int>::iterator it = a.begin(); it != a.end(); ++it)
    cout << *it << endl;

a.begin()

是一个迭代器，指向首个元素

a.end()

是一个迭代器，指向最后一个元素之后的位置

上述迭代器具备自增运算符，自增时迭代器将移至下一个元素。

迭代器类似于指针，若对其使用解引用运算符，即

*it

，就能获取对应的值。

3.2 为何需要迭代器？

许多数据结构并非线性（比如红黑树），针对这类非线性数据结构，索引没有实际意义。无法利用索引来遍历整个数据结构。

迭代器的功能在于定义特定数据结构的遍历方法，通过迭代器的增加或减少，表示当前遍历的位置，从而能够有效遍历非线性结构。

比如，set 的底层实现基于红黑树，我们无法借助索引来访问元素。然而，借助迭代器，我们可以遍历 set 中的元素：

for (set<int>::iterator it = st.begin(); it != st.end(); ++it)
    cout << *it << endl;

3.3 迭代器应用

以 vector 容器为例，其迭代器功能较为全面：

.begin()

：起始迭代器

.end()

：结束迭代器

.rbegin()

：逆向起始迭代器

.rend()

：逆向结束迭代器

迭代器

+

整型：将迭代器向后推进

迭代器

-

整型：将迭代器向前推进

迭代器

++

：将迭代器向后推进一位

迭代器

--

：将迭代器向前推进一位

迭代器

-

迭代器：两个迭代器间的距离

迭代器

prev(it)

：返回 it 的前一个迭代器

next(it)

：返回 it 的后一个迭代器

对于其他容器，由于其结构特点，上述功能可能并不完全适用（例如 set 的迭代器不支持求距离的操作）

3.4 常见疑问

.end()

和

.rend()

指向的位置是没有实际意义的值

对于长度为 10 的数组：

for (int i = 0; i < 10; i++)

，第 10 位是无法访问的

对于长度为 10 的容器：

for (auto it = a.begin(); it != a.end(); ++it)

，.end 是无法访问的

不同容器的迭代器功能可能存在差异

迭代器具体分为正向、逆向和双向，每个容器支持的运算符也可能各不相同，因此不同容器的迭代器细节可能会有所不同。

执行删除操作时需谨慎

为何 3 没被删除？

vector<int> a{1, 2, 3, 4};
for (auto it = a.begin(); it != a.end(); ++it)
    if (*it == 2 || *it == 3)
        a.erase(it);
// a = [1, 3, 4]

为何出现 RE 错误？

vector<int> a{1, 2, 3, 4};
for (auto it = a.begin(); it != a.end(); ++it)
    if (*it == 4)
        a.erase(it);

建议：除非必要，否则避免使用迭代器操作容器。（遍历与访问无关）

4 常用算法

4.1 总览

标记了勾选的将在本次详细讨论，其他则是在算法竞赛中推荐学习的，未在列表中出现的基本在比赛中较少使用。

（许多函数功能简单，自己也能迅速编写，但使用这些函数可以提高代码的可读性，这一点在比赛中至关重要）

算法库 Algorithm

[ ]

count()

[ ]

find()

[ ]

fill()

[x]

swap()

[x]

reverse()

[ ]

shuffle()

C++11

[x]

unique()

[x]

sort()

[x]

lower_bound()

/

upper_bound()

[x]

max()

/

min()

[ ]

max_element()

/

min_element()

[ ]

prev_permutation()

/

next_permutation()

数学函数 cmath

[x]

abs()

[x]

exp()

[x]

log()

/

log10()

/

log2()

[x]

pow()

[x]

sqrt()

[ ]

sin()

/

cos()

/

tan()

[ ]

asin()

/

acos()

/

atan()

[ ]

sinh()

/

cosh()

/

tanh()

[ ]

asinh()

/

acosh()

/

atanh()

C++11

[x]

ceil()

/

floor()

[x]

round()

C++11

数值算法 numeric

[ ]

iota()

C++11

[ ]

accumulate()

[x]

gcd()

C++17

[x]

lcm()

C++17

伪随机数生成 random

[ ]

mt19937

[ ]

random_device()

4.2

swap()

交换两个变量的值

使用示例

template< class T >
void swap( T& a, T& b );

int a = 0, b = 1;
swap(a, b);
// now a = 1, b = 0

int arr[10] {0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
swap(arr[4], arr[6]);
// now arr = {0, 1, 2, 3, 6, 5, 4, 7, 8, 9}

注意事项

此 swap 参数采用引用形式，无需像 C 语言那样传递地址。

4.3

sort()

使用快速排序对一个可迭代对象进行排序

使用示例

template< class RandomIt, class Compare >
void sort( RandomIt first, RandomIt last, Compare comp );

默认按升序排序

vector<int> arr{1, 9, 1, 9, 8, 1, 0};
sort(arr.begin(), arr.end());
// arr = [0, 1, 1, 1, 8, 9, 9]

若需按降序排列，则需传入比较器。

vector<int> arr{1, 9, 1, 9, 8, 1, 0};
sort(arr.begin(), arr.end(), greater<int>());
// arr = [9, 9, 8, 1, 1, 1, 0]

若需完成特殊排序，则需自定义比较器。

比较器函数返回值为布尔类型，参数为需要比较的两个元素。假设我们定义的比较操作为??：

若?a?b，则比较器函数应返回

true

若?a??b，则比较器函数应返回

false

注意：

若?a=b，比较器函数必须返回

false

bool cmp(pair<int, int> a, pair<int, int> b) {
    if (a.second != b.second)
    return a.second < b.second;
    return a.first > b.first;
    }
    int main() {
    vector<pair<int, int>> arr{{1, 9}, {2, 9}, {8, 1}, {0, 0}};
    sort(arr.begin(), arr.end(), cmp);
    }

// arr = [(0, 0), (8, 1), (2, 9), (1, 9)]
}

4.4

lower_bound()

/

upper_bound()

在已升序排列的元素中，利用二分搜索查找特定元素，返回匹配元素的迭代器位置。
如果未找到，则返回尾部迭代器。

lower_bound()

: 查找?≥x?的首个元素的位置

upper_bound()

: 查找?>x?的首个元素的位置
如何寻找?≤x?/?<x?的首个元素呢？
?>x?的首个元素的前一元素（如果存在）即为?≤x?的首个元素
?≥x?的首个元素的前一元素（如果存在）即为?<x?的首个元素
返回的是迭代器，要转换成下标索引怎么办？减去起始迭代器即可。

用法示例

template< class ForwardIt, class T >
ForwardIt lower_bound( ForwardIt first, ForwardIt last, const T& value );

vector<int> arr{0, 1, 1, 1, 8, 9, 9};
vector<int>::iterator it = lower_bound(arr.begin(), arr.end(), 7);
int idx = it - arr.begin();
// idx = 4

我们常写成一行：

vector<int> arr{0, 1, 1, 1, 8, 9, 9};
idx = lower_bound(arr.begin(), arr.end(), 7) - arr.begin(); // 4
idx = lower_bound(arr.begin(), arr.end(), 8) - arr.begin(); // 4
idx = upper_bound(arr.begin(), arr.end(), 7) - arr.begin(); // 4
idx = upper_bound(arr.begin(), arr.end(), 8) - arr.begin(); // 5

4.5

reverse()

反转一个可迭代对象的元素顺序
用法示例

template< class BidirIt >
void reverse( BidirIt first, BidirIt last );

vector<int> arr(10);
iota(arr.begin(), arr.end(), 1);
// 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
reverse(arr.begin(), arr.end());
// 10, 9, 8, 7, 6, 5, 4, 3, 2, 1

4.6

max()

/

min()

返回最大值 / 最小值的数值
用法示例

int mx = max(1, 2); // 2
int mn = min(1, 2); // 1

自 C++11 之后，可以使用列表初始化语法传递一个列表，这样就能同时为多个元素求最大值而不必嵌套：

// Before C++11
int mx = max(max(1, 2), max(3, 4)); // 4
int mn = min(min(1, 2), min(3, 4)); // 1

// After C++11
int mx = max({1, 2, 3, 4}); // 4
int mn = min({1, 2, 3, 4}); // 1

4.7

unique()

移除数组中相邻的重复元素，数组长度保持不变，但有效数据缩短，返回有效数据结尾的迭代器。
例如：[1,1,4,5,1,4]→[1,4,5,1,4,?―]，下划线处为返回的迭代器指向。

template< class ForwardIt >
ForwardIt unique( ForwardIt first, ForwardIt last );

用法示例
单独使用 unique 无法实现去重效果，因为它仅移除相邻的重复元素。但如果序列已排序，那么它可以去重。
然而，去重后，序列末尾将出现一些无效数据：[1,1,2,4,4,4,5]→[1,2,4,5,?―,?,?]，为了删除这些无效数据，需结合 erase.
最终，为 vector 去重的写法为：

vector<int> arr{1, 2, 1, 4, 5, 4, 4};
sort(arr.begin(), arr.end());
arr.erase(unique(arr.begin(), arr.end()), arr.end());

4.8 数学函数
所有函数参数均支持

int

/

long long

/

float

/

double

/

long double

公式
示例
f(x)=|x|

abs(-1.0)

f(x)=e^x

exp(2)

f(x)=ln x

log(3)

f(x,y)=x^y

pow(2, 3)

f(x)=sqrt(x)

sqrt(2)

f(x)=floor(x)

ceil(2.1)

f(x)=ceil(x)

floor(2.1)

f(x)=round(x)

round(2.1)

注意事项
由于浮点误差，某些数学函数的行为可能不符合预期，导致错误答案。如果你的操作数均为整型，那么采用以下写法更为稳妥。
原始地址：
https://codeforces.com/blog/entry/107717
?a/b?
避免使用：

floor(1.0 * a / b)

推荐使用：

a / b

?a/b?
避免使用：

ceil(1.0 * a / b)

推荐使用：

(a + b - 1) / b

（?a/b?=(a+b-1)/b?）
?a?
避免使用：

(int) sqrt(a)

推荐使用：二分查找
https://io.zouht.com/7.html
a/b
避免使用：

pow(a, b)

推荐使用：快速幂
https://io.zouht.com/18.html
?log2(a)?
避免使用：

log2(a)

推荐使用：

__lg

（不规范，但在竞赛中适用）/

bit_width

（C++20 可用）

4.9

gcd()

/

lcm()

（C++17）返回最大公约数 / 最小公倍数

int x = gcd(8, 12); // 4
int y = lcm(8, 12); // 24

如果不是 C++17，但使用 GNU 编译器（g++），则可以使用内建函数

__gcd()

.
当然，

gcd

/

lcm

函数也容易编写，直接编写即可（欧几里得算法）：

int gcd(int a, int b)
{
    if (!b)
        return a;
    return gcd(b, a % b);
}

int lcm(int a, int b)
{
    return a / gcd(a, b) * b;
}

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

分享0 收藏0 回帖

关键词：学习笔记 STL 习笔记 include Vector

相关内容：C++笔记学习