发帖
雷达卡
LU 分解
以下是关于 LU 分解（LU decomposition）的详细总结，包括定义、存在的条件、计算步骤及其特性。
1. 定义
LU 分解是指将一个 \( n \times n \) 的矩阵 \( A \) 分解为两个矩阵的乘积：
\[ A = LU \]
其中，\( L \) 是单位下三角矩阵，意味着其对角线上的所有元素均为 1；而 \( U \) 是上三角矩阵。这种分解方式在数值线性代数领域极为重要，常被应用于解决线性方程组、计算行列式以及求逆矩阵等问题。
2. 存在性条件
并非所有的矩阵都能进行 LU 分解。其基本条件是矩阵 \( A \) 的所有前导主子式（leading principal minors）都不为零，即：
\[ \det(A_{1:k,1:k}) \neq 0, \quad k=1,2,\dots,n \]
这里 \( A_{1:k,1:k} \) 指的是由矩阵 \( A \) 的前 \( k \) 行和前 \( k \) 列组成的子矩阵。此条件确保了在执行高斯消元法的过程中不会遇到除以零的情况。如果某个前导主子式为零，则需使用列或行主元选取技术，从而得到形式为 \( PA = LU \) 的分解，其中 \( P \) 为置换矩阵。
3. 计算方法
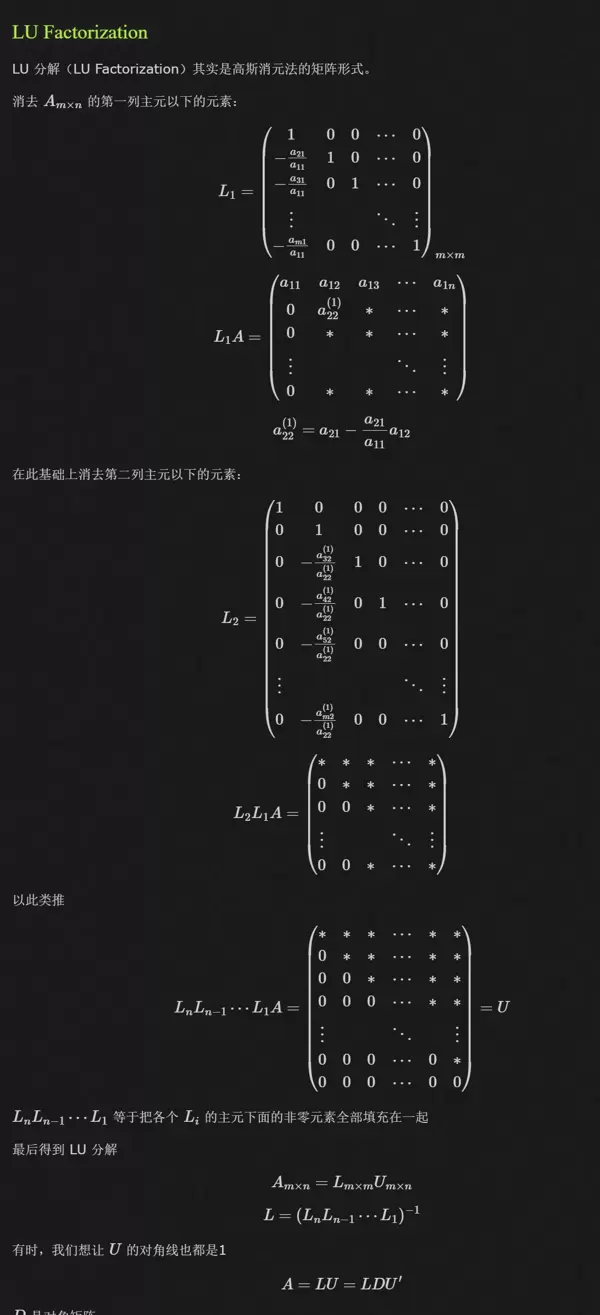
LU 分解实际上是将高斯消元法中的每一步操作用矩阵形式表示出来。
3.1 高斯消元过程
通过消除 \( A \) 矩阵中对角线下方的元素，将其转化为上三角矩阵：
\[ A \xrightarrow{\text{elimination}} U \]
在此过程中使用的消元因子（multiplier）为：
\[ l_{ik} = \frac{a_{ik}^{(k)}}{a_{kk}^{(k)}} \]
这些消元因子构成了矩阵 \( L \) 的非对角元素。
3.2 具体分解形式
将一次消元视为矩阵乘法：
\[ E_1 A = A^{(1)}, \quad E_2 A^{(1)} = A^{(2)}, \dots \]
每个 \( E_k \) 实际上是在单位矩阵的基础上加上了一个用于将某列下三角置零的消元向量。最终结果为：
\[ E_{n-1}\cdots E_1 A = U \]
取其逆运算：
\[ A = E_1^{-1} E_2^{-1} \cdots E_{n-1}^{-1} U \]
由于每个 \( E_k^{-1} \) 都是单位下三角矩阵，将它们相乘即可得到 \( L \)。
4. 唯一性
当要求 \( L \) 为单位下三角矩阵（即对角线元素为 1）时，LU 分解是唯一的。
5. 应用于线性方程组求解
对于线性方程组 \( Ax=b \)，可以通过以下步骤求解：
- 首先对 \( A \) 进行分解，使其成为 \( LU \) 形式；
- 接着解下三角方程 \( Ly = b \)；
- 最后解上三角方程 \( Ux = y \)。
这种方法的时间复杂度为 \( O(n^3) \)，特别适用于需要对相同的 \( A \) 多次求解不同 \( b \) 的情况，能够显著提高计算效率。
6. 带主元的分解（部分主元选取）
为了确保数值稳定性和防止直接分解失败，可以使用部分主元选取技术，即将矩阵 \( A \) 调整为 \( PA = LU \) 的形式，其中 \( P \) 为置换矩阵，表示行交换。这可以确保算法的稳定性，并避免除以零的问题。
在满足存在性的条件下，通过不断执行高斯消元法，最终会得到一个上三角矩阵，然后通过左乘 \( L \) 矩阵，就可以将 \( A \) 分解成上下三角矩阵的形式。
Cholesky 分解
当分解的对象是一个正定对称矩阵时，左乘操作和右乘操作将分别实现上下对称的消元操作，这样不仅简化了计算过程，还使计算量减少了一半。
京公网安备 11010802022788号
