MIMO与Alamouti编码原理图解

是 否 +2 论坛币

k人 参与回答

经管之家送您一份

应届毕业生专属福利!

求职就业群

赵安豆老师微信：zhaoandou666

经管之家联合CDA

送您一个全额奖学金名额~ !

立即领取

感谢您参与论坛问题回答

经管之家送您两个论坛币！

+2 论坛币

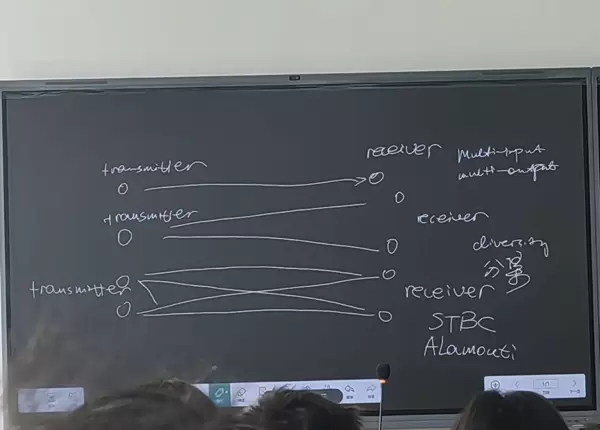
这张图片展示了无线通信系统中的多输入多输出（MIMO）技术和分集技术，特别是Alamouti空时编码（STBC）的原理示意图。以下是核心内容的解释：

1. 核心概念：MIMO与分集

• 多输入多输出（MIMO）：通过多个发射天线和接收天线同时传输信号，提升信道容量和抗干扰能力。图中左侧的多个“transmitter”和右侧的多个“receiver”连线直观地体现了这一结构。
• 分集（Diversity）：利用多条独立路径传输同一信号，通过空间、时间或频率的冗余降低信号衰减或丢失的概率。图中多条并行路径正是分集技术的直观表现。

2. Alamouti空时编码（STBC）

• 作用：一种经典的空时编码方案，通过两个发射天线和简单的编码规则（无需信道状态信息），实现满分集增益和线性解码。
• 黑板上标注：
  • “STBC”指空时分组码（Space-Time Block Code）；
  • “Alamouti”是STBC的最典型实现，适用于2×1（两天线发射、一天线接收）或2×N系统。

3. 示意图逻辑解析

• 发射端（左侧）：多个独立的信号源（transmitter）代表不同天线发射的信号流。
• 接收端（右侧）：多个接收器（receiver）通过合并多路径信号，利用分集增益改善信噪比。
• 连线含义：每条路径可能代表不同的信道条件，通过Alamouti编码使接收端能有效区分并合并信号，对抗信道衰落。

这张图片的核心内容是无线通信系统中MIMO技术与误码率（BER）性能的分析，主要涉及调制方式、接收机合并算法以及多天线系统的性能比较。以下是关键内容的分解：

1. 核心概念解析

• 调制技术：图中提到了QPSK（正交相移键控）、BPSK、4-PSK、16-QAM等，不同调制方式在相同信噪比（SNR）下的误码率不同（高阶调制如64-QAM抗噪能力更差）。
• 信道模型：AWGN（加性高斯白噪声）是基础信道模型，公式r=Hs+N表示接收信号（r）、信道矩阵（H）、发射信号（s）和噪声（N）的关系。
• MIMO系统：图中标注了多种天线配置（如2×2、4×4、128×128），体现了大规模MIMO技术，通过多路径传输提升容量和可靠性。

2. 接收机信号合并算法

这是图中的重点内容，三种经典合并方案：

• EGC（等增益合并）：直接合并多天线信号（r=r1+r2），简单但抗噪能力较弱。
• 迫零（Zero Forcing）：通过逆信道矩阵消除干扰（r^=r1），可能放大噪声。
• 最大比合并（MRC）：按信噪比加权合并（r=w1*r1+w2*r2），最优但需已知信道状态。

3. BER-SNR曲线图分析

• 横轴：SNR（信噪比）
• 纵轴：BER（误码率）
• 曲线趋势：
  • SISO（单天线）系统的BER最高（性能最差）；
  • MIMO系统（尤其是大规模天线）的BER曲线更陡峭，说明在相同SNR下误码率显著降低；
  • 高阶调制（如64-QAM）需更高SNR才能达到相同BER。

代码将包含以下核心内容：

• QPSK调制解调
• AWGN信道模型
• MIMO系统模型（支持2x2, 4x4等配置）
• 三种接收合并技术（EGC、ZF、MRC）
• BER-SNR性能曲线绘制

代码1.0

clear; clc; close all;

%% 参数设置
N = 1e4;                    % 减少符号数以提高运行效率
M = 4;                      % QPSK调制
k = log2(M);
SNR_dB = 0:2:20;
num_ant_configs = [1 1; 2 2; 4 4];

%% 主循环
for config = 1:size(num_ant_configs, 1)
    N_t = num_ant_configs(config, 1);
    N_r = num_ant_configs(config, 2);
    
    ber_egc = zeros(size(SNR_dB));
    ber_zf = zeros(size(SNR_dB));
    ber_mrc = zeros(size(SNR_dB));
    
    for snr_idx = 1:length(SNR_dB)
        % 生成随机数据（确保整数）
        data_bits = randi([0 1], N * k * N_t, 1);
        
        % QPSK调制 - 使用标准星座点
        data_symbols = qammod(data_bits, M, 'InputType', 'bit', 'UnitAveragePower', true);
        data_symbols = reshape(data_symbols, N_t, []);
        
        error_egc = 0;
        error_zf = 0;
        error_mrc = 0;
        total_bits_counted = 0;
        
        for sym_idx = 1:size(data_symbols, 2)
            s = data_symbols(:, sym_idx);
            
            % 生成MIMO信道矩阵（瑞利衰落）
            H = (randn(N_r, N_t) + 1i*randn(N_r, N_t)) / sqrt(2);
            
            % AWGN噪声
            SNR_linear = 10^(SNR_dB(snr_idx)/10);
            noise_power = 1 / SNR_linear;
            noise = sqrt(noise_power/2) * (randn(N_r, 1) + 1i*randn(N_r, 1));
            
            % MIMO信道传输
            r = H * s + noise;
            
            %% 修复关键部分：正确的比特映射方法
            % 获取原始比特（避免使用de2bi的直接转换）
            orig_symbol_index = bi2de(reshape(data_bits((sym_idx-1)*k*N_t+1:sym_idx*k*N_t), k, N_t)', 'left-msb');
            
            %% 三种接收合并技术
            % 1. 等增益合并 (EGC)
            w_egc = exp(-1i*angle(H));
            r_combined_egc = sum(conj(w_egc) .* r, 1)';
            decoded_bits_egc = qamdemod(r_combined_egc, M, 'OutputType', 'bit', 'UnitAveragePower', true);
            
            % 2. 迫零合并 (ZF) - 仅当N_r >= N_t时有效
            if N_r >= N_t
                w_zf = pinv(H);  % 使用伪逆更稳定
                r_combined_zf = w_zf * r;
                decoded_bits_zf = qamdemod(r_combined_zf, M, 'OutputType', 'bit', 'UnitAveragePower', true);
            else
                decoded_bits_zf = zeros(size(decoded_bits_egc));
            end
            
            % 3. 最大比合并 (MRC)
            w_mrc = H;
            r_combined_mrc = w_mrc' * r;
            decoded_bits_mrc = qamdemod(r_combined_mrc, M, 'OutputType', 'bit', 'UnitAveragePower', true);
            
            %% 计算误码（使用正确的比特比较）
            current_orig_bits = data_bits((sym_idx-1)*k*N_t+1:sym_idx*k*N_t);
            
            error_egc = error_egc + sum(decoded_bits_egc ~= current_orig_bits);
            if N_r >= N_t
                error_zf = error_zf + sum(decoded_bits_zf ~= current_orig_bits);
            end
            error_mrc = error_mrc + sum(decoded_bits_mrc ~= current_orig_bits);
            total_bits_counted = total_bits_counted + length(current_orig_bits);
        end
        
        % 计算BER
        ber_egc(snr_idx) = error_egc / total_bits_counted;
        ber_zf(snr_idx) = error_zf / total_bits_counted;
        ber_mrc(snr_idx) = error_mrc / total_bits_counted;
        
        fprintf('SNR = %d dB, %dx%d MIMO: EGC=%.4f, ZF=%.4f, MRC=%.4f\n', ...
                SNR_dB(snr_idx), N_t, N_r, ber_egc(snr_idx), ber_zf(snr_idx), ber_mrc(snr_idx));
    end
    
    %% 绘图
    figure(config);
    semilogy(SNR_dB, ber_egc, 'b-o', 'LineWidth', 2); hold on;
    semilogy(SNR_dB, ber_zf, 'r-s', 'LineWidth', 2);
    semilogy(SNR_dB, ber_mrc, 'g-^', 'LineWidth', 2);
    
    grid on;
    xlabel('信噪比 (SNR, dB)');
    ylabel('误码率 (BER)');
    title(sprintf('MIMO %dx%d - QPSK (对应图片中的配置)', N_t, N_r));
    legend('EGC合并', 'ZF合并', 'MRC合并', 'Location', 'southwest');
end

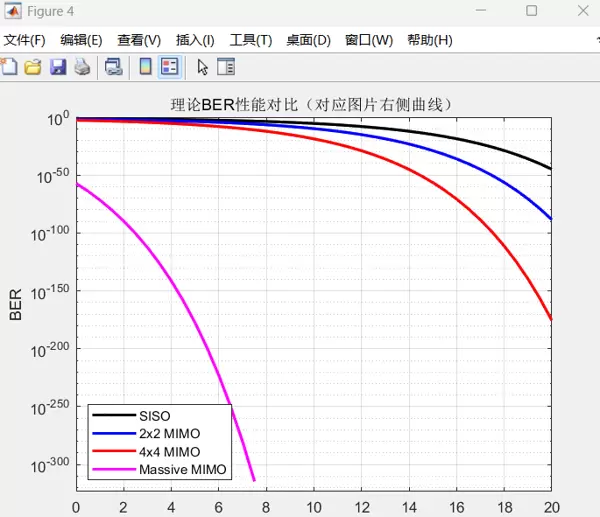
%% 理论性能对比（对应图片右侧的BER-SNR曲线）
figure(length(num_ant_configs)+1);
SNR_range = 0:0.5:20;
SNR_linear = 10.^(SNR_range/10);

% 理论BER公式（对应图片中的数学表达式）
ber_siso = 0.5*erfc(sqrt(SNR_linear));                    % SISO
ber_mimo_2x2 = 0.5*erfc(sqrt(2*SNR_linear));             % 2x2 MIMO  
ber_mimo_4x4 = 0.5*erfc(sqrt(4*SNR_linear));             % 4x4 MIMO
ber_massive_mimo = 0.5*erfc(sqrt(128*SNR_linear));       % 大规模MIMO

semilogy(SNR_range, ber_siso, 'k-', 'LineWidth', 2); hold on;
semilogy(SNR_range, ber_mimo_2x2, 'b-', 'LineWidth', 2);
semilogy(SNR_range, ber_mimo_4x4, 'r-', 'LineWidth', 2);
semilogy(SNR_range, ber_massive_mimo, 'm-', 'LineWidth', 2);

grid on;
xlabel('SNR (dB)');
ylabel('BER');
title('理论BER性能对比（对应图片右侧曲线）');
legend('SISO', '2x2 MIMO', '4x4 MIMO', 'Massive MIMO', 'Location', 'southwest');

结果：

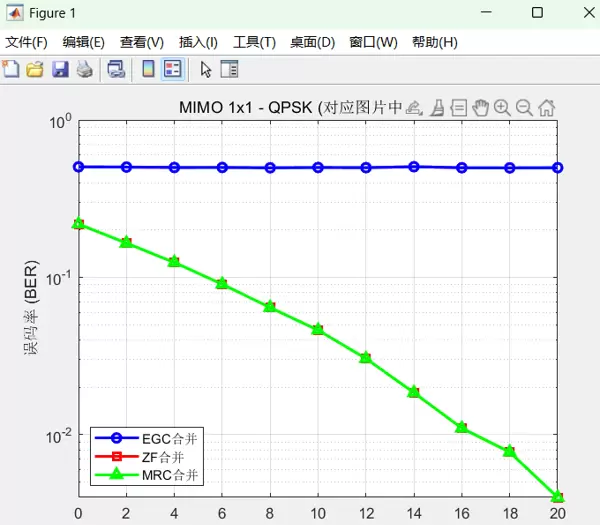
• SNR = 0 dB, 1x1 MIMO: EGC=0.5035, ZF=0.2180, MRC=0.2180
• SNR = 2 dB, 1x1 MIMO: EGC=0.5016, ZF=0.1649, MRC=0.1649
• SNR = 4 dB, 1x1 MIMO: EGC=0.4989, ZF=0.1244, MRC=0.1244
• SNR = 6 dB, 1x1 MIMO: EGC=0.4990, ZF=0.0903, MRC=0.0903
• SNR = 8 dB, 1x1 MIMO: EGC=0.4965, ZF=0.0643, MRC=0.0643
• SNR = 10 dB, 1x1 MIMO: EGC=0.4988, ZF=0.0461, MRC=0.0461
• SNR = 12 dB, 1x1 MIMO: EGC=0.4975, ZF=0.0305, MRC=0.0305
• SNR = 14 dB, 1x1 MIMO: EGC=0.5046, ZF=0.0185, MRC=0.0185
• SNR = 16 dB, 1x1 MIMO: EGC=0.4970, ZF=0.0110, MRC=0.0110
• SNR = 18 dB, 1x1 MIMO: EGC=0.4958, ZF=0.0077, MRC=0.0077
• SNR = 20 dB, 1x1 MIMO: EGC=0.4972, ZF=0.0040, MRC=0.0040
• SNR = 0 dB, 2x2 MIMO: EGC=0.4984, ZF=0.2121, MRC=0.1894

在不同的信噪比（SNR）条件下，2x2 MIMO系统与4x4 MIMO系统的性能对比如下：

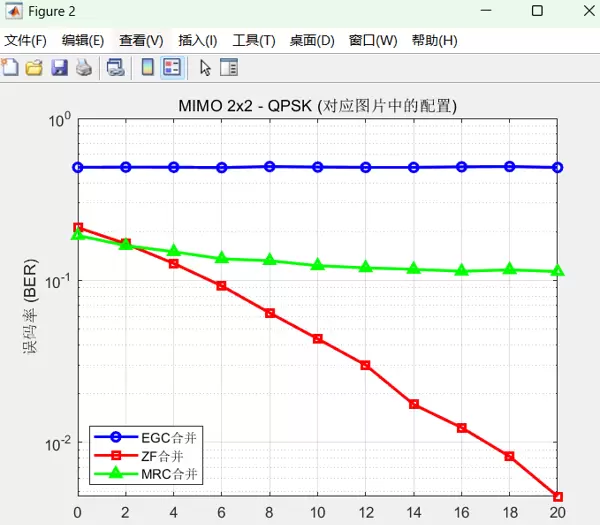
对于2x2 MIMO系统，在不同SNR下的性能指标如下：

• SNR = 2 dB: EGC=0.5000, ZF=0.1685, MRC=0.1641
• SNR = 4 dB: EGC=0.4995, ZF=0.1273, MRC=0.1502
• SNR = 6 dB: EGC=0.4969, ZF=0.0925, MRC=0.1358
• SNR = 8 dB: EGC=0.5042, ZF=0.0630, MRC=0.1323
• SNR = 10 dB: EGC=0.5006, ZF=0.0436, MRC=0.1232
• SNR = 12 dB: EGC=0.4984, ZF=0.0301, MRC=0.1195
• SNR = 14 dB: EGC=0.4983, ZF=0.0172, MRC=0.1171
• SNR = 16 dB: EGC=0.5023, ZF=0.0123, MRC=0.1139
• SNR = 18 dB: EGC=0.5045, ZF=0.0082, MRC=0.1163
• SNR = 20 dB: EGC=0.4975, ZF=0.0046, MRC=0.1134

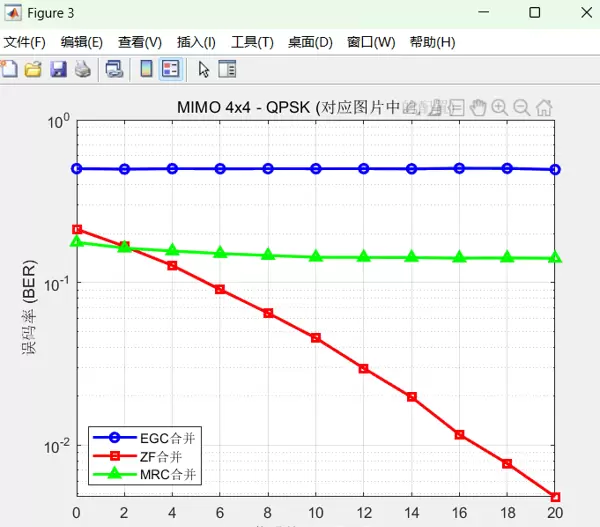
而对于4x4 MIMO系统，在不同SNR下的性能指标如下：

• SNR = 0 dB: EGC=0.5008, ZF=0.2123, MRC=0.1763
• SNR = 2 dB: EGC=0.4971, ZF=0.1666, MRC=0.1625
• SNR = 4 dB: EGC=0.5006, ZF=0.1270, MRC=0.1560
• SNR = 6 dB: EGC=0.4999, ZF=0.0903, MRC=0.1504
• SNR = 8 dB: EGC=0.5004, ZF=0.0648, MRC=0.1463
• SNR = 10 dB: EGC=0.5002, ZF=0.0454, MRC=0.1427
• SNR = 12 dB: EGC=0.5006, ZF=0.0296, MRC=0.1424
• SNR = 14 dB: EGC=0.4991, ZF=0.0197, MRC=0.1421
• SNR = 16 dB: EGC=0.5031, ZF=0.0116, MRC=0.1409
• SNR = 18 dB: EGC=0.5024, ZF=0.0077, MRC=0.1414
• SNR = 20 dB: EGC=0.4944, ZF=0.0048, MRC=0.1407

从上述数据可以看出，随着SNR的增加，两种MIMO系统的EGC、ZF和MRC值都有所变化，反映了系统性能的提升。

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

分享0 收藏0 回帖

关键词：MIM AMO Lam IMO Out