发帖
雷达卡
一、作用域的基本概念
在编程中，作用域指的是变量或函数可以被访问的有效范围。不同的作用域决定了变量的可见性和生命周期。
以下代码展示了不同作用域中变量的使用情况：
#include<stdio.h>
int main() {
// a 和 b 定义在 main 函数的作用域内
// 因此在整个 main 函数中都可以使用
int a = 1, b = 2;
for (int i = 0; i < 3; i++) {
// c 和 d 局部于 for 循环内部的作用域
// 只能在该 {} 内部进行访问
int c = 1, d = 2;
// 由于 for 在 main 的作用域中，因此可以访问 a 和 b
printf("a = %d, b = %d\n", a, b);
// 同时也可以访问当前作用域内的 c 和 d
printf("c = %d, d = %d\n", c, d);
}
// 离开 for 循环后仍可访问 a 和 b
printf("a = %d, b = %d\n", a, b);
// 下列语句将报错，因为 c 和 d 已超出其作用域
// printf("c = %d, d = %d\n", c, d);
return 0;
}
作用域：定义的变量，作用的区域执行结果如下所示：
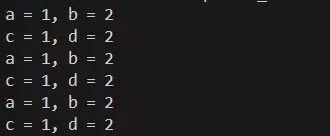
当内外层作用域存在同名变量时，内部作用域会屏蔽外部变量。例如：
#include<stdio.h>
int main() {
// 外部作用域中的 a 和 b
int a = 1, b = 2;
for (int i = 0; i < 3; i++) {
// 内部作用域重新定义了 a 和 b
int a = 3, b = 4;
// 此处访问的是内部变量
printf("in for: a = %d, b = %d\n", a, b);
}
// 循环结束后恢复对外部变量的访问
printf("outside : a = %d, b = %d\n", a, b);
return 0;
}
该程序的输出结果为：
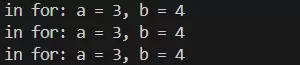
二、函数的使用与设计
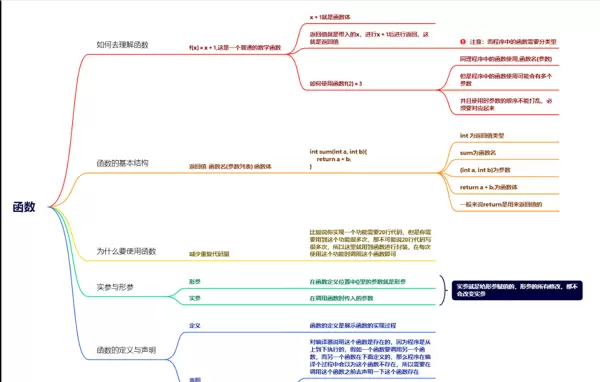
1. 函数的定义与调用方式
函数是实现特定功能的代码块，其基本结构包括返回类型、函数名、参数列表和函数体。
示例代码如下：
#include <stdio.h>
#include <math.h>
// 定义一个整型返回值的函数，用于计算两数之和
int sum(int a, int b) {
return a + b;
}
// 根据 flag 值选择对 x 执行 sqrt(x) 或 x*x 操作
// 返回值可能为浮点型，因此使用 double 类型
double function_1(int flag, int x) {
if (flag == 1)
return sqrt(x);
else if (flag == 2)
return x * x;
else
return 0; // 防止非法输入导致未定义行为
}
// 无返回值函数：打印 n 次 "hello world"
void printf_hello_world(int n) {
for (int i = 0; i < n; i++) {
printf("hello world\n");
}
return; // 显式结束函数
}
int main() {
// 调用 sum 函数并输出结果
printf("3 + 4 = %d\n", sum(3, 4));
int flag, x;
printf("intput flag and x\n");
scanf("%d%d", &flag, &x);
// 注意格式符 %lf 对应 double 类型
printf("function_1 = %lf\n", function_1(flag, x));
int n;
printf("input n\n");
scanf("%d", &n);
printf_hello_world(n);
return 0;
}
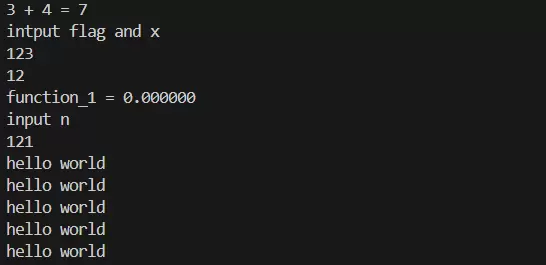
2. 引入函数结构的意义
为何要采用函数化编程？主要原因包括：
- 提高代码复用性，避免重复编写相同逻辑；
- 增强程序可读性，使主流程更清晰；
- 便于调试与维护，功能模块独立隔离；
- 支持分层开发，多人协作更加高效。
以数学运算为例，若需多次处理某个区间内的等差序列（起始值 start，结束值 end，公差 d），将其封装成函数即可反复调用，提升整体开发效率。
// 等差数列求和函数的封装与应用
int function_sum(int start, int end, int d) {
int n = (end - start) / d + 1; // 计算项数
int num = start + (n - 1) * d; // 确定末项
int sum = (start + num) * n / 2; // 应用求和公式
return sum;
}
int main() {
// 示例：计算不同等差数列的和
// 公差为1，从1加到100
int sum1 = (1 + 100) * 100 / 2;
// 公差为2，从1开始直到不超过100
int n2 = (100 - 1) / 2 + 1;
int num2 = 1 + (n2 - 1) * 2;
int sum2 = (1 + num2) * n2 / 2;
// 公差为17，从30到34534
int n3 = (34534 - 30) / 17 + 1;
int num3 = 30 + (n3 - 1) * 17;
int sum3 = (30 + num3) * n3 / 2;
printf("%d %d %d\n", sum1, sum2, sum3);
// 观察发现，每次计算都需要多行重复代码
// 因此可将该逻辑封装成函数，提升代码复用性和可读性
// 使用封装后的函数重新计算
printf("%d ", function_sum(1, 100, 1));
printf("%d ", function_sum(1, 100, 2));
printf("%d\n", function_sum(30, 34534, 17));
return 0;
}
通过上述实现可以看出，使用函数能够有效减少冗余代码，使主函数结构更清晰、逻辑更直观。
3. 形参与实参的区别
以下代码用于演示函数调用过程中参数传递的特点：
#include <stdio.h>
void function_A(int a, int b) { // a 和 b 为形参
a = a + 1;
b = b * 2;
printf("in function_A : a = %d, b = %d\n", a, b);
return;
}
int main() {
int a = 1, b = 2;
function_A(a, b); // a 和 b 作为实参传入
printf("in main : a = %d, b = %d\n", a, b);
return 0;
}
运行结果表明：在函数内部对形参的修改不会影响主函数中实参的原始值。这说明实参向形参传递的是值的副本，而非变量本身。
4. 函数的声明与定义
#include <stdio.h>
// 函数前置声明，告知编译器函数的存在
int func_b(int x);
int func_a(int x) {
// 若无func_b的声明，编译器在未见其定义时会报错
if (x == 1) return func_b(x);
printf("func_a : x * 2 = %d\n", x * 2);
return 0;
}
int func_b(int x) {
if (x == 2) return func_a(x);
printf("func_b : x * 3 = %d\n", x * 3);
return 0;
}
int main() {
// 本程序展示了两个函数相互调用的情形：
// func_a 接收1则调用func_b；否则输出x*2
// func_b 接收2则调用func_a；否则输出x*3
func_a(2);
func_a(1);
return 0;
}
函数的“定义”描述了其具体行为，而“声明”则是提前告诉编译器该函数的签名信息（如返回类型、参数列表），以便在函数定义之前就能被调用。这对于实现函数间的交叉调用至关重要。
5. 递归函数的概念与实现
递归是一种函数调用自身的技术，常用于解决具有自相似结构的问题。关键要素包括：
- 递归出口（终止条件），防止无限递归
- 每次递归应缩小问题规模
示例：计算阶乘
#include <stdio.h>
int func(int n) {
if (n == 1) return 1; // 递归终止条件
return n * func(n - 1); // 向下递归
}
int main() {
int n;
while (scanf("%d", &n) != EOF) { // 支持连续输入，Ctrl+C结束
printf("!%d = %d\n", n, func(n));
}
return 0;
}
递归执行过程图解如下：
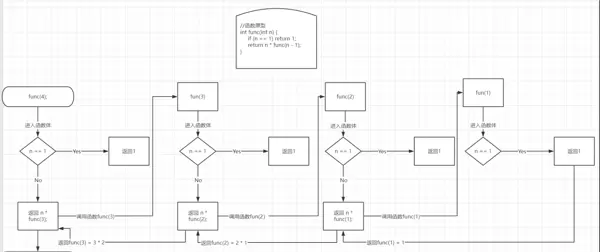通过流程图可以清楚地看到函数逐层调用与返回的过程，有助于理解递归的工作机制。
练习建议：尝试编写一个递归函数来求解斐波那契数列的第n项。
斐波那契数列是一组特殊的数字序列：1，1，2，3，5，8，13，21，34，55，89……从第3项开始，每一项的值都等于前两项之和。这个规律构成了该数列的核心定义。
代码实现与递归解析
#include <stdio.h>
int func(int n) {
if (n == 1 || n == 2) return 1;
return func(n - 1) + func(n - 2);
}
int main() {
int n;
scanf("%d", &n);
printf("func(%d) = %d\n", n, func(n));
return 0;
}
在理解上述递归函数时，可以这样思考：当调用 func(n)（其中 n > 2）时，函数会返回 func(n-1) + func(n-2) 的结果。这一过程不断触发新的函数调用，直到参数变为1或2——这两个条件作为递归的终止出口。随后，程序开始逐层回溯，将每层的结果相加，最终得到原始调用的返回值。
为了更清晰地掌握其执行流程，建议手动绘制递归调用树。通过图形化方式展示每一层的调用与返回关系，有助于深入理解递归机制的工作原理。
欧几里得算法简介
对于两个整数 a 和 b，它们的最大公约数通常记作 gcd(a, b)，即能同时整除 a 和 b 的最大正整数。例如，32 和 24 的最大公约数为 8。
该算法的核心公式为：
gcd(a, b) = gcd(b, a % b)
解释：gcd(a,b)返回值就是a和b的最大公约数
现在需要证明: b 和 a % b的最大公约数是 a 和 b 的公约数。
先证明b 和 a % b的最大公约数也是a 和 b 的公约数公式证明过程
证明一：
假设
gcd(b, a % b) = c c是b和a % b 的最大公约数
设 b = x * c 因为c为b的公约数，所以设b等于x倍c
设 a - k * b = y * c
这个式子的推到过程
a % b是求 a / b 的余数
a / b的余数 + k倍b = a
所以 a % b = a - k * b
y * c就是y倍他们的最大公约数c
现在得到两个式子
b = x * c
a = k * b + y * c
将上面的式子带入到下面式子
a = k * x * c + y * c
a = c * (k * x + y)
最终得到
b = x * c
a = (k * x + y) * c
可以证明a和b也有c这个公约数此部分说明了 b 与 a % b 的最大公约数同样是 a 与 b 的公约数之一。
现在来证明b和a % b的最大公约数也是a 和 b 的最大公约数证明二：
根据上面的推理得到
b = x * c
a = (k * x + y) * c
如何去证明b和a % b的最大公约数也是a 和 b 的最大公约数
通过证明1开始的设
b = x * c
a - k * b = y * c
可以的得到
gcd(x, y) = 1
因为b 和 a % b的最大公约数就是c
所以x和y是互斥的，他们的最大公约数就是1
所以只需要证明 x 和 (k * x + y)是互斥的,也就是他们的最大公约数为1,那么c就是a和b的最大公约数
反证法:
gcd(x, k * x + y) = d
设 x = n * d
设 k * x + y = m * d
那么 y = m * d - k * x
带入x = n * d
y = d * (m - k * n)
因为gcd(x, y) = 1
那么d只能为1，如果d为2或者其他数gcd(x, y)是不可能等于1的
最终证明 b和a % b的最大公约数也是a 和 b 的最大公约数结合“证明一”与“证明二”，可得出结论：等式 gcd(a, b) = gcd(b, a % b) 成立。
算法代码实现
#include<stdio.h>
int gcd_1(int a, int b) {
if (b == 0) return a;
return gcd_1(b, a % b);
}
int gcd_2(int a, int b) {
return b ? gcd_2(b, a % b) : a;
}
int main() {
int a, b;
scanf("%d%d", &a, &b);
printf("gcd_1(%d, %d) = %d\n", a, b, gcd_1(a, b));
printf("gcd_2(%d, %d) = %d\n", a, b, gcd_1(a, b));
return 0;
}
关于递归出口为何设置为 b == 0，可以通过一个实例来理解：
- 设 a = 12，b = 8
- 则有：gcd(12, 8) = gcd(8, 12 % 8) = gcd(8, 4)
- 继续：gcd(8, 4) = gcd(4, 8 % 4) = gcd(4, 0)
- 此时 b = 0，满足递归终止条件，返回 a = 4
由此可见，当 b 为 0 时，当前的 a 值即为原始 a 和 b 的最大公约数。需要注意的是，这里的 a 在不同递归层级中代表不同的数值，最终返回的是最深层调用中的 a 值。
此外，gcd_2 函数使用了三元运算符（? :），其逻辑与 gcd_1 完全一致，仅写法更为简洁。由于非零值视为真，零值视为假，因此可以直接以 b 作为判断条件。
扩展欧几里得算法（附加内容）
贝祖等式指出：对于任意两个整数 a 和 b，存在整数 x 和 y，使得以下等式成立：
a × x + b × y = gcd(a, b) = c
该等式的解可通过扩展欧几里得算法求出。其推导过程依赖于递归回溯的思想。
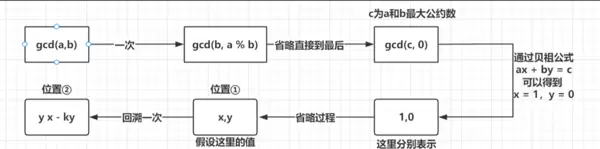
关键问题在于：已知某一步的解 x 和 y（标记为位置①），如何反推出前一步对应的 x 和 y（位置②）？由于算法最后一步已知，需逆向推导。将最后一项视为当前位置①，则倒数第二项为位置②。利用此方法，可以从末尾逐步向前计算，最终获得初始状态下的 x 和 y。
证明：
位置①
因为 a % b = a - k * b
所以可以得到等式
b * x + (a % b) * y = c
b * x + (a - k * b) * y = c
b * x + a * y - k * b * y = c
b * (x - k * y) + a * y = c
所以通过贝祖等式可以得到位置②对应的x和y
_x = y, _y = x - k * y;根据数学推导，前一项的解可通过如下关系更新：
_x = y
_y = x - k * y
其中 k 是当前步的商（即 a / b 的整数部分）。基于此规则，可通过递归实现获取初始系数 x 和 y 的完整代码：
#include<stdio.h>
// 使用全局变量便于在整个作用域内访问
// 只要在定义之后，任何函数均可读取或修改其值
// 最终结果即为递归回溯完成后的最终取值
int x, y, _x, _y; // 分别用于存储当前层与下一层递归中的 x 和 y 值
int gcd_up(int a, int b) {
if (b == 0) {
x = 1;
y = 0;
return a;
}
int c = gcd_up(b, a % b); // 递归调用，进入下一层
// 根据扩展欧几里得算法的推导关系进行系数更新
_x = y; // 当前层的 x 等于下一层的 y
int k = a / b; // 计算商 k
_y = x - k * y; // 利用公式计算当前层的 y
// 回溯前更新全局变量，供上层使用
x = _x;
y = _y;
return c;
}
int main() {
int a, b;
scanf("%d%d", &a, &b);
int c = gcd_up(a, b);
printf("x = %d, y = %d, gcd(%d, %d) = %d\n", x, y, a, b, c);
return 0;
}
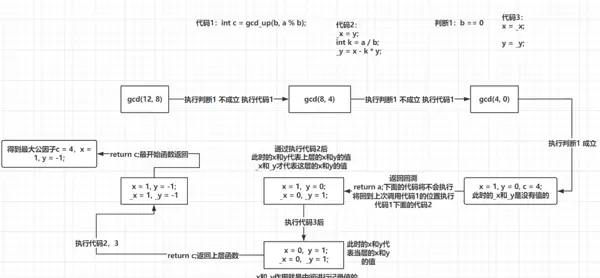
以下是代码执行流程的思维导图说明：
掌握该结构后，在后续熟练过程中，此类递归逻辑将能自然地在脑海中构建出来。
递归与回溯练习题解析：
本题目对初学者可能有一定难度，建议在学习完数组相关内容后再进行尝试。一旦理解此题逻辑，便基本掌握了递归与回溯的核心思想。
题目来源：海贼OJ 235
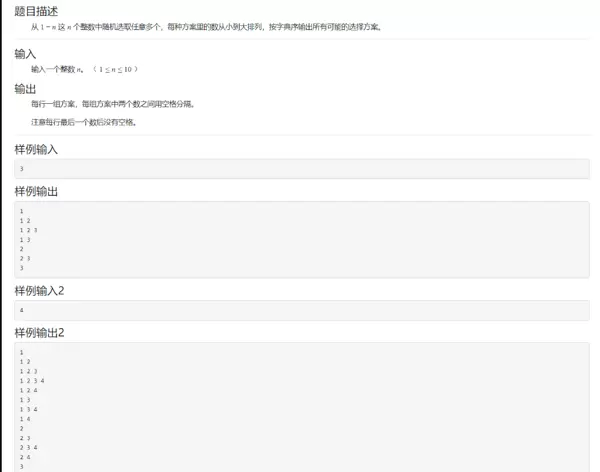#include <stdio.h>
int n;
int num[15]; // 用于存储当前已选择的数字序列
int s = 0; // 表示当前序列长度（栈顶指针）
int func(int x) {
if (x > n) return 0; // 递归终止条件：起始位置超出范围
for (int i = x; i <= n; i++) {
num[s++] = i; // 将当前数字加入路径
// 打印当前子集
for (int j = 0; j < s; j++) {
if (j != 0) printf(" ");
printf("%d", num[j]);
}
printf("\n");
func(i + 1); // 递归处理下一个可选起点
// 回溯：恢复状态
s--;
}
return 0;
}
int main() {
scanf("%d", &n);
func(1);
return 0;
}
6. 可变参数函数的实现
下面展示如何编写一个支持可变参数的函数，用于求多个整数中的最大值。
#include <stdio.h>
#include <stdarg.h>
#include <stdint.h>
// 参数 n 指明后续实际传入的可变参数个数
int max_int(int n, ...) {
va_list args; // 定义一个指向可变参数列表的指针
va_start(args, n); // 初始化参数列表，从 n 之后开始读取
int ans = INT32_MIN; // 初始化最大值为最小可能整数值
for (int i = 0; i < n; i++) {
int a = va_arg(args, int); // 依次获取每个 int 类型的可变参数
if (a > ans) ans = a; // 更新最大值
}
va_end(args); // 清理参数列表（良好习惯）
return ans;
}
int main() {
printf("max_int(%d, %d, %d, %d) = %d\n", 2, 4, 6, 1, max_int(4, 2, 4, 6, 1));
printf("max_int(%d, %d, %d, %d, %d) = %d\n", 10, 4, 6, 1, 88, max_int(5, 10, 4, 6, 1, 88));
return 0;
}
7. 主函数的参数形式
#include <stdio.h>
int main(int argc, char *argv[]) {
printf("argc = %d\n", argc); // 输出命令行参数总数
// 遍历并打印所有参数内容
for (int i = 0; i < argc; i++) {
printf("argv[%d] = %s\n", i, argv[i]);
}
return 0;
}
通过运行程序可以观察到：
- `argc` 用于记录命令行输入的参数数量；
- `argv` 是一个字符串数组，保存了每一个参数的具体内容。
京公网安备 11010802022788号
