我们通过代码实现来验证高数中常见的求导法则,观察其实际运行结果是否与理论一致:
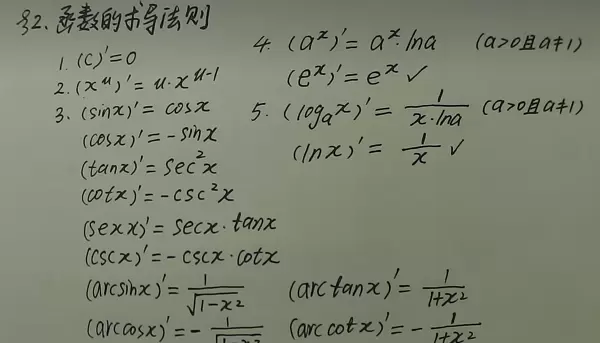
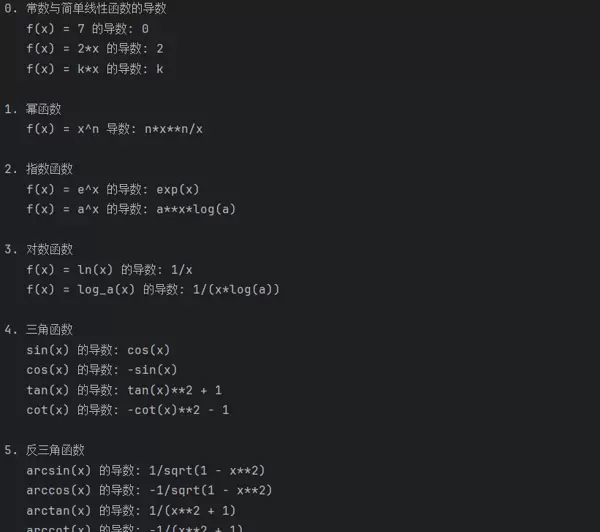 从运行结果可以看出,程序计算出的内容与数学推导的结论完全吻合。我们可以参考以下公式进一步确认:
从运行结果可以看出,程序计算出的内容与数学推导的结论完全吻合。我们可以参考以下公式进一步确认:


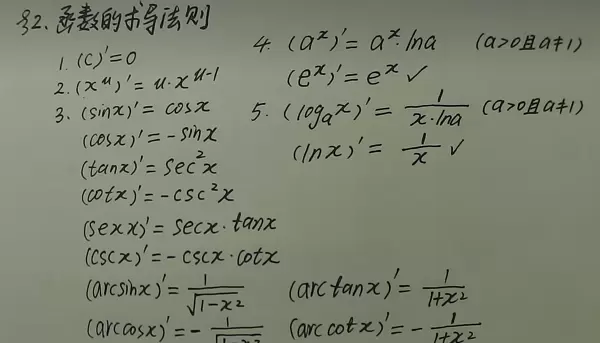
import sympy as sp
# 定义符号变量
x = sp.symbols('x')
print("0. 常数与简单线性函数的导数")
# 常数函数:比如 f(x) = 7
f0_const = 7
print(" f(x) = 7 的导数:", sp.diff(f0_const, x))
# 线性函数:f(x) = 2x
f0_linear = 2 * x
print(" f(x) = 2*x 的导数:", sp.diff(f0_linear, x))
# 也可以用更一般的形式:f(x) = k*x
k = sp.symbols('k')
f0_general_linear = k * x
print(" f(x) = k*x 的导数:", sp.diff(f0_general_linear, x))
print()
# 后续是之前的基本函数(可选保留)
n = sp.symbols('n')
print("1. 幂函数")
print(" f(x) = x^n 导数:", sp.diff(x**n, x))
print()
a = sp.symbols('a', positive=True)
print("2. 指数函数")
print(" f(x) = e^x 的导数:", sp.diff(sp.exp(x), x)) #在 SymPy中,exp(x) 表示e^x
print(" f(x) = a^x 的导数:", sp.diff(a**x, x)) #在SymPy中,log(a)指以e为底的对数,数学上通常记为 ln(a)
print()
print("3. 对数函数")
print(" f(x) = ln(x) 的导数:", sp.diff(sp.log(x), x))
print(" f(x) = log_a(x) 的导数:", sp.diff(sp.log(x, a), x))
print()
print("4. 三角函数")
print(" sin(x) 的导数:", sp.diff(sp.sin(x), x))
print(" cos(x) 的导数:", sp.diff(sp.cos(x), x))
print(" tan(x) 的导数:", sp.diff(sp.tan(x), x))
print(" cot(x) 的导数:", sp.diff(sp.cot(x), x))
print()
print("5. 反三角函数")
print(" arcsin(x) 的导数:", sp.diff(sp.asin(x), x))
print(" arccos(x) 的导数:", sp.diff(sp.acos(x), x))
print(" arctan(x) 的导数:", sp.diff(sp.atan(x), x))
print(" arccot(x) 的导数:", sp.diff(sp.acot(x), x)) 从运行结果可以看出,程序计算出的内容与数学推导的结论完全吻合。我们可以参考以下公式进一步确认:
从运行结果可以看出,程序计算出的内容与数学推导的结论完全吻合。我们可以参考以下公式进一步确认:






 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







