【永磁同步电机】基于simulink的永磁同步电机PMSM矢量控制 1.依据PMSM的数学模型...

是 否 +2 论坛币

k人 参与回答

经管之家送您一份

应届毕业生专属福利!

求职就业群

赵安豆老师微信：zhaoandou666

经管之家联合CDA

送您一个全额奖学金名额~ !

立即领取

感谢您参与论坛问题回答

经管之家送您两个论坛币！

+2 论坛币

基于Simulink的永磁同步电机（PMSM）矢量控制实现

在研究永磁同步电机（PMSM）控制系统的过程中，利用Simulink搭建矢量控制模型是一种高效且直观的方法。本文将介绍如何基于PMSM的数学模型，在Simulink中实现完整的矢量控制策略，涵盖建模、双闭环控制设计以及状态变量的估算方法。

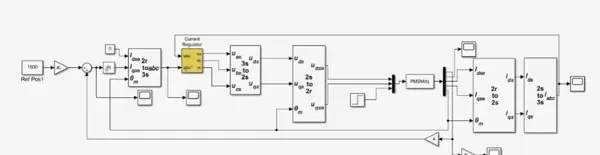
1. 搭建PMSM电机系统模型

矢量控制的核心基础是准确的电机数学模型。为了在仿真环境中真实反映PMSM的动态行为，需依据其电压方程、磁链关系和机械运动方程构建对应的Simulink模型。该模型通常包括定子电压方程、转子磁链表达式以及描述转速与电磁转矩之间关系的动力学方程。

通过合理配置这些方程模块，可以在仿真中精确模拟电机在不同工况下的响应特性，为后续控制器设计提供可靠平台。

% PMSM电压方程
Vd = Rs * Id + Ld * dId/dt - omega * Lq * Iq;
Vq = Rs * Iq + Lq * dIq/dt + omega * (Ld * Id + psi_f);

2. 双闭环PI解耦控制策略设计

在控制结构上，采用经典的双闭环架构：外环为转速环，内环为电流（转矩）环，两者均使用PI调节器进行反馈控制。这种结构能够实现d轴与q轴之间的有效解耦，从而提升系统的动态响应性能和稳态精度。

其中，转速外环根据实际转速与设定值的偏差输出期望的q轴电流指令；而转矩内环则通过调节d、q轴电压实现对电流的快速跟踪。该控制逻辑可通过Simulink中的PID Controller模块或自定义S函数实现。

% 转速外环PI调节器
Kp_speed = 0.1;
Ki_speed = 0.01;
speed_error = speed_ref - speed_actual;
torque_ref = Kp_speed * speed_error + Ki_speed * integral(speed_error);

3. 基于EKF与AEKF的状态估计算法

在无传感器控制应用中，获取转子的电角度和机械转速是一个关键问题。为此，引入了扩展卡尔曼滤波（EKF）及其改进版本——自适应扩展卡尔曼滤波（AEKF）算法，用于在线估算难以直接测量的状态变量。

EKF通过对非线性系统进行局部线性化处理，结合噪声统计信息，实现对转子位置和速度的高精度估计。AEKF进一步优化了噪声协方差的自适应调整机制，增强了系统在参数变化或外部扰动下的鲁棒性。

% EKF算法
function [theta_est, omega_est] = EKF(Id, Iq, Vd, Vq, Ts)
    % 状态方程
    x_est = [theta_est; omega_est];
    F = [1 Ts; 0 1];
    x_pred = F * x_est;
    
    % 观测方程
    H = [1 0];
    y_pred = H * x_pred;
    
    % 更新步骤
    K = P_pred * H' / (H * P_pred * H' + R);
    x_est = x_pred + K * (y_meas - y_pred);
    P_est = (eye(2) - K * H) * P_pred;
    
    theta_est = x_est(1);
    omega_est = x_est(2);
end

4. 观测器实现方式与代码规范性说明

在Simulink中实现上述观测器时，采用了静态变量定义的方式编写核心算法模块。这种方式不仅提高了代码的可读性和模块化程度，也便于后期调试与功能扩展。

整个项目文档完整，函数命名清晰，注释详尽，符合工程开发标准，有助于用户理解算法原理并进行个性化修改。

% 静态变量定义
persistent theta_est omega_est;
if isempty(theta_est)
    theta_est = 0;
    omega_est = 0;
end

总结

本方案展示了从PMSM数学建模到矢量控制实现的完整流程，结合双闭环PI控制与先进的状态估计算法，构建了一个高性能的仿真控制系统。整个过程突出了理论与实践的结合，适用于教学研究及工程原型开发。

通过对各模块的合理组织与参数整定，能够有效提升永磁同步电机的控制精度与运行稳定性。希望此内容能为相关领域的学习者和开发者提供有价值的参考。

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

分享0 收藏0 回帖

关键词：simulink 同步电机 数学模型 link msm