斜齿轮时变啮合刚度的Matlab计算程序解析
在机械传动系统设计中,斜齿轮的动态特性至关重要,而时变啮合刚度正是影响其振动与噪声行为的核心参数之一。本文将介绍如何利用Matlab实现斜齿轮时变啮合刚度的数值计算,并对关键代码逻辑进行说明。
理论基础概述
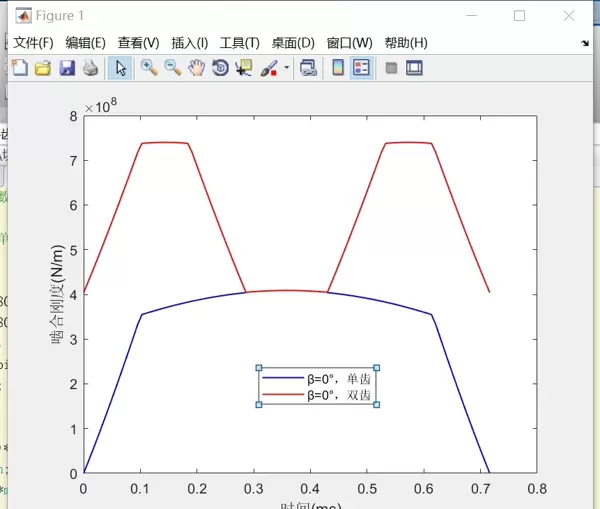
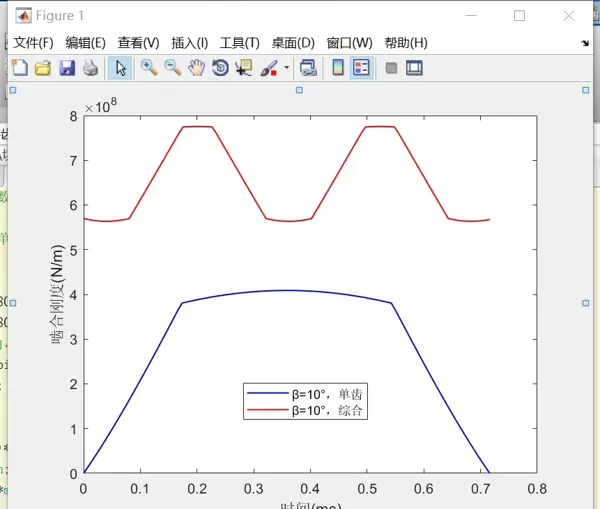
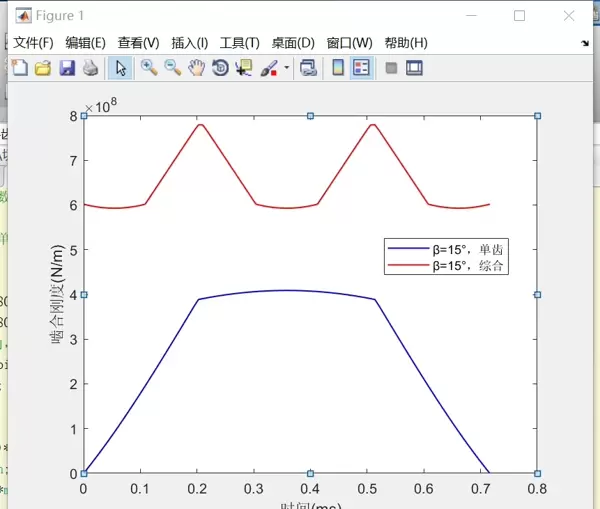
斜齿轮在运转过程中,由于轮齿逐对进入和退出啮合,导致啮合刚度呈现周期性变化。这种时变特性受多种几何参数影响,包括模数、齿数、螺旋角、齿宽等。这些参数共同决定了齿轮副在不同啮合相位下的刚度响应。
核心计算流程
以下为基于Matlab的简化计算框架,涵盖从参数设定到结果可视化的完整过程。
1. 参数初始化
程序首先定义基本齿轮参数:模数、主动轮与从动轮的齿数(num_teeth1)、螺旋角(helix_angle)以及齿宽。这些是后续所有计算的基础输入,如同构建模型的“地基”。例如,模数直接影响齿形尺寸与承载能力;齿数决定传动比;螺旋角则关系到啮合平稳性和轴向力分布。
modulenumteeth2facewidth2. 中间变量求解
根据已知参数,计算两齿轮的基圆半径(base_circle_radius1 和 base_circle_radius2)。基圆是齿轮啮合理论中的重要概念,许多力学分析,如接触线长度、法向力方向等,均依赖于基圆信息。
3. 啮合位置与刚度数组设置
通过linspace或类似方法生成一个从0到 2*pi / num_teeth1 的啮合位置向量(mesh_position),用以模拟一个完整的啮合周期。随后预分配一个相同长度的数组用于存储各位置对应的刚度值(mesh_stiffness)。该操作有助于提升Matlab运行效率,避免动态扩展数组带来的性能开销。
linspacemeshpositionstiffness4. 刚度循环计算
在for循环中,采用赫兹接触理论估算每一啮合点的局部刚度。假设施加恒定接触力(contact_force),实际应用中此值应结合传递扭矩、转速等工况精确确定。接着,依据基圆半径与齿宽推导出两个关键系数,进而合成当前相位下的啮合刚度值。
需注意:此处为理想化简化模型,真实情况还需考虑齿面修形、摩擦、多齿耦合及三维有限元修正等因素。
fork1k2stiffness(i)5. 结果可视化
使用plot函数绘制时变啮合刚度曲线,清晰展现刚度随啮合相位的变化趋势。同时添加坐标轴标签与标题,增强图表可读性,便于工程分析与报告展示。
plot% 定义基本参数
module = 2; % 模数
num_teeth1 = 20; % 主动轮齿数
num_teeth2 = 40; % 从动轮齿数
helix_angle = 15; % 螺旋角(度)
face_width = 30; % 齿宽
% 计算一些中间变量
base_circle_radius1 = module * num_teeth1 / 2 * cosd(helix_angle);
base_circle_radius2 = module * num_teeth2 / 2 * cosd(helix_angle);
% 这里假设一个简单的啮合位置范围,从0到一个啮合周期
mesh_position = linspace(0, 2 * pi / num_teeth1, 100);
% 预分配存储刚度的数组
mesh_stiffness = zeros(size(mesh_position));
for i = 1:length(mesh_position)
% 简单的赫兹接触理论计算刚度(这里是高度简化版,实际更复杂)
contact_force = 100; % 假设一个接触力,实际应根据工况计算
k1 = 1 / (base_circle_radius1 * face_width);
k2 = 1 / (base_circle_radius2 * face_width);
mesh_stiffness(i) = 2 * contact_force / (k1 + k2);
end
% 绘制时变啮合刚度曲线
figure;
plot(mesh_position, mesh_stiffness);
xlabel('Mesh Position (rad)');
ylabel('Mesh Stiffness (N/m)');
title('Time - Variant Mesh Stiffness of Helical Gear');总结与展望
本文提供的Matlab程序虽为简化的理论模型,但已能有效反映斜齿轮时变啮合刚度的基本变化规律。作为研究起点,它为深入理解齿轮动力学提供了直观工具。未来可在该基础上引入更精确的非线性刚度模型、考虑制造误差与装配偏差的影响,进一步逼近真实工况。




 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







