发帖
雷达卡
在数值分析中，问题的敏感性与导数密切相关。对于函数的导数倒数 dx/dy 而言，其绝对值越小，表示系统对输入变化越敏感。
二分法是求解方程根的一种基础方法，中学阶段已有涉及，适用于连续函数且在区间两端函数值异号的情形。
不动点迭代法基于将原方程 f(x) = 0 转化为等价形式 x = g(x)，此时满足 x = g(x) 的点称为不动点。该方法收敛的关键在于：在真实根 x* 附近，若 |g'(x*)| < 1，则迭代过程收敛；且 |g'(x*)| 越小，收敛速度越快。当 g'(x*) = 0 时，可实现二次收敛，即收敛速度显著提升。
以方程 f(x) = x - x - 2 = 0 为例，其根为 x = 2 和 x = -1。将其转化为四种不同的 g(x) 形式进行分析：
- 若 g(x) = x - 2，则 g'(2) = 4 > 1，迭代发散；
- 若 g(x) = √(x + 2)，则 g'(2) = 1/4 < 1，呈现线性收敛，并从单侧趋近于根；
- 若 g(x) = 1 + 2/x，则 g'(2) = -1/2，绝对值小于1，同样线性收敛，但迭代点在根两侧交替逼近；
- 若 g(x) = (x + 2)/(2x - 1)，则 g'(2) = 0，达到二阶收敛，速度最快。
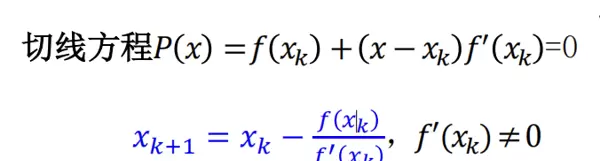
牛顿迭代法是一种高效的求根方法，通过在每一步使用泰勒展开的一阶近似来构造迭代公式：
x^(k+1) = x^k - f(x^k)/f'(x^k)
该方法具有较快的局部收敛性，通常为二次收敛。然而，它对导数的连续性要求较高，且每次迭代需计算导数，计算成本较大。
割线法可视为牛顿法的有限差分替代版本，利用前两次迭代点的函数值构造斜率代替导数，避免了显式求导，适合导数不易计算的情况。
反二次插值法（Inverse Quadratic Interpolation）则利用三个历史迭代点及其函数值，通过拉格朗日插值反推下一个估计值，常用于多项式根的高效逼近。
具体实现步骤如下：
1. 输入与初始化
给定三个初始近似解：
abc以及对应的函数值：
fa = f(a)fb = f(b)fc = f(c)2. 计算中间变量
定义辅助变量：
u = fb / fc
v = fb / fa
w = fa / fc
随后计算：
p = v * w * u - w * c - b * (1 - u) * (b - a)
q = (w - 1)(u - 1)(v - 1)
新的估计值为：
new_estimate = b + p / q
new_estimate3. 更新迭代点集
用新估计值替换原有三点中距离它最远的那个点，保持三个点的有序性，以便下一轮迭代继续使用。
abc重复上述过程直至满足收敛条件。
雅可比矩阵（Jacobian Matrix）是非线性方程组求解中的核心工具，由所有函数关于所有变量的一阶偏导数组成，形式如下：
[ f/x f/x ... f/x ]
J = [ f/x f/x ... f/x ]
[ ]
[ f/x f/x ... f/x ]
对于非线性方程组：
f(x, x, …, x) = 0
f(x, x, …, x) = 0
...
f(x, x, …, x) = 0
可通过构造相应的不动点格式进行迭代求解：
x^(k+1) = g(x^k, x^k, …, x^k)
x^(k+1) = g(x^k, x^k, …, x^k)
...
x^(k+1) = g(x^k, x^k, …, x^k)
而牛顿法在多维情形下的推广基于向量函数 f: → 的一阶泰勒展开：
f(x + s) ≈ f(x) + J_f(x)s
令近似等于零，解得修正量 s 满足：
J_f(x^k)s = -f(x^k)
从而得到迭代格式：
x^(k+1) = x^k + s = x^k - [J_f(x^k)] f(x^k)
此方法在初值足够接近真解时表现出良好的收敛性能，但需要求解线性方程组或矩阵求逆，计算开销较大。
此外，牛顿下山法通过对步长引入控制因子，增强算法的全局稳定性，防止因初始值不佳导致发散。
京公网安备 11010802022788号
