必要观测量的概念与应用
在测量平差中,为了唯一确定网中各点的位置,必须进行一定数量的观测。这些最少必需的观测值个数被称为“必要观测量”。从数学角度理解,它表示在不考虑观测误差的前提下,能够求解出所有未知参数所需的最小观测数目。必要观测量是经典平差理论中的核心概念之一,直接影响多余观测数 r = n - t 的计算和平差模型的构建。
在传统测绘工作中,常见控制网包括高程控制网和平面控制网。针对不同类型的网型,其必要观测量的确定方法有所不同。本文将依次对水准网、测角网、测边网及边角网等典型结构进行分析,并结合图示说明必要观测量个数 t 的推导过程。
一、高程控制网中的必要观测量
在水准网中,目标是通过水准测量获取各待定点的高程平差值。由于高程系统需要一个基准参考,因此是否存在已知高程点会直接影响必要观测量的计算方式。
1.1 含已知点的水准网
当网中存在 m 个已知高程点和 p 个待定点时,整个水准网共包含 m + p 个水准点。此时,因已有高程基准,只需确定每个待定点的高程即可,故必要观测量个数等于待定点的数量:
t = p
以下为两种典型网型示例:
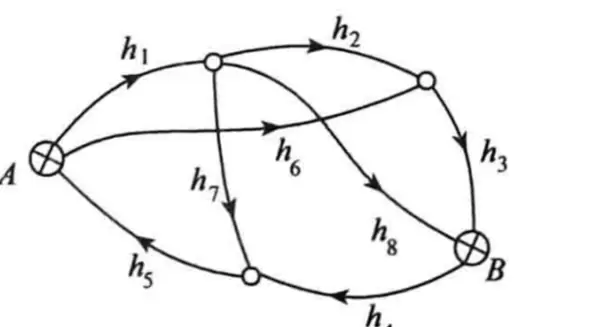
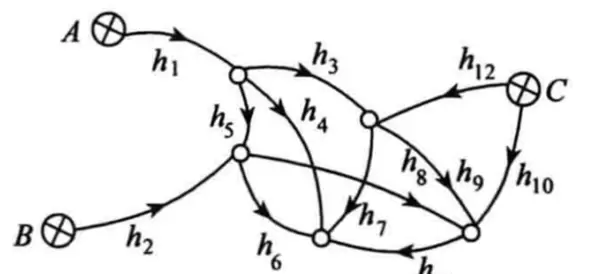
注: 图片来源《误差理论与测量平差基础习题集》(第二版)
左图所示:观测总数 n = 8,必要观测量 t = 3,多余观测 r = 5;右图:n = 12,t = 5,r = 7。
1.2 不含已知点的水准网
若全网无任何已知高程点,设共有 m 个水准点,则缺乏统一的高程基准。此时需人为选定一个点作为参考基准(如设定其高程为零),其余 m - 1 个点相对于该基准进行确定。
因此,必要观测量个数为:
t = m - 1
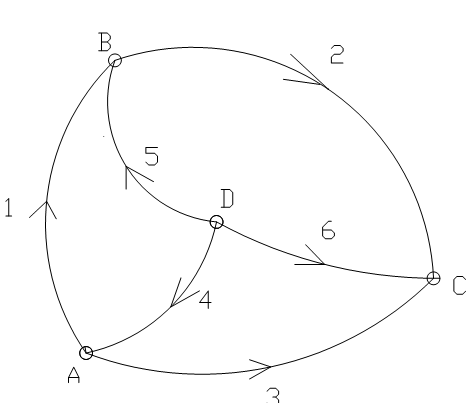
本例中,n = 6,t = 3,r = 3,符合上述公式。
二、平面控制网中的必要观测量
平面控制网主要包括测角网、测边网以及边角同测网三种类型。其中,测边网与边角网在基准需求上具有相似性。为便于统一表述,引入以下符号:
- p:总点数
- Q:全部起算数据总数
- q:多余起算数据个数(文中用于逻辑判断)
2.1 测角网
测角网以角度观测为主,利用三角关系推算各点坐标。要完全确定一个平面图形的位置、大小和方向,需满足以下三类基准条件:
- 位置基准(2个):任一点的坐标 (x, y)
- 方位基准(1个):某条边的方位角 α
- 长度基准(1个):某条边的边长 S
这四项基准等价于两个已知点的坐标信息。根据起算数据是否充足,分为两种情况:
① 起算数据充分(Q ≥ 4)
当已知条件足以提供完整的四个基准参数时,必要观测量为:
t = 2p - Q
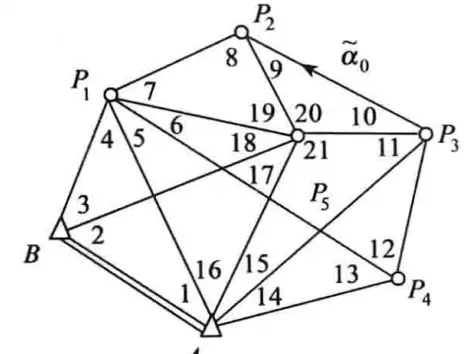
注: 案例来源《误差理论与测量平差基础习题集》(第二版)
图中包含两个已知点坐标及一个已知方位角,共5个起算数据,属于此类情形。代入得:t = 2×7 - 5 = 9。
② 起算数据不足或无已知点
当无法提供完整基准时,需假设建立4个基准参数,此时必要观测量为:
t = 2p - 4
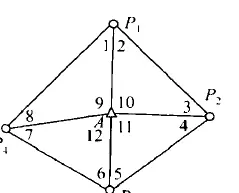
注: 案例来源《测量平差问题中必要观测数的确定》
该网仅有一个已知点,基准不完整,故采用此式:t = 2×5 - 4 = 6。
2.2 测边网与边角网
测边网的观测值全为边长,而边角网则同时包含角度和边长观测。两者在基准需求方面基本一致,区别在于边长本身自带尺度信息,因此无需额外指定长度基准。
其所需基准为:
- 位置基准(2个):某点坐标 (x, y)
- 方位基准(1个):某边方位角 α
共计三个独立基准参数。
据此可分为两种情形:
① 起算数据不足、刚好或恰好满足三个基准
此时必要观测量为:
t = 2p - 3
② 起算数据多于必要基准(即 Q > 3)
应使用实际已知数据数量参与计算:
t = 2p - Q
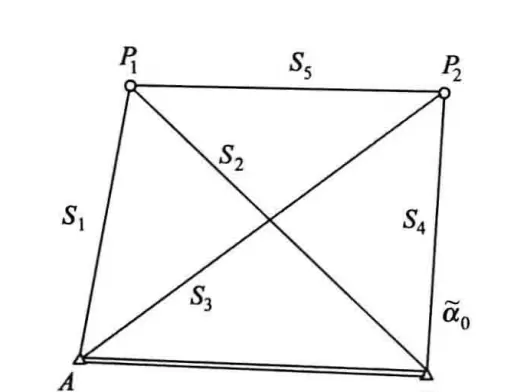
注: 案例来源《误差理论与测量平差基础习题集》(第二版)
图为测边网,含两个已知点(提供4个坐标参数)和一个已知方位角,总计 Q = 5,属第二种情况。p = 4,故 t = 2×4 - 5 = 3。
补充说明:单一导线网
对于由 m 个待定点组成的单一导线,至少需观测 m+2 个转折角和 m+1 段边长,因此其必要观测量为:
t = 2m + 3
注意:此情况不适用于前述测边网或边角网的一般分类规则。
三、总结
本文系统梳理了高程控制网与平面控制网中必要观测量的判定原则。无论是水准网中的高程基准依赖,还是平面网中坐标、方位与尺度基准的组合要求,均体现了必要观测量在平差建模中的关键作用。正确识别各类网型的基准条件并合理计算 t 值,是确保平差结果科学性和可靠性的前提。希望相关内容能为测量工程实践提供有益参考。
参考文献
- 姚宜斌,邱卫宁.测量平差问题中必要观测数的确定[J].测绘通报,2007,(03):14-15+18.
- 宁伟,欧吉坤,张发顺.测量平差中必要观测数确定的再探讨[J].测绘通报,2010,(10):11-13+20.
- 武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础习题集 [M]. 武汉: 武汉大学出版社, 2015.




 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







