机器学习可解释性实操

是 否 +2 论坛币

k人 参与回答

经管之家送您一份

应届毕业生专属福利!

求职就业群

赵安豆老师微信：zhaoandou666

经管之家联合CDA

送您一个全额奖学金名额~ !

立即领取

感谢您参与论坛问题回答

经管之家送您两个论坛币！

+2 论坛币

本文简要探讨了可解释机器学习的研究背景，并借助 Python 中的 sklearn 工具库，初步实践了几种典型的事后可解释性方法。这些技术手段在实际建模与模型分析过程中具有重要的应用价值。

一、研究背景与基础知识

（一）可解释性提出的动因

近年来，深度学习等复杂模型在人工智能的多个领域取得了显著成果，几乎涵盖了人类能完成或难以完成的任务场景。然而，相较于线性回归、决策树等结构清晰的传统模型，深度学习常被视为“黑盒”系统——我们无法直观理解其内部决策机制。

即便对于传统模型，若能通过深入分析揭示特征间的交互关系，也能极大提升模型的理解深度和应用效果。因此，为应对“黑盒”带来的信任与调试难题，学术界提出了“可解释机器学习”的概念。

所谓解释，即以易于理解的方式阐明某个过程或结果。对机器学习而言，可解释性意味着模型具备被人类认知的能力，能够将从输入到输出的预测逻辑转化为清晰、有条理的规则表达。

值得注意的是，可解释性本身具有主观性：不同用户对“解释清楚”的标准不一，难以用统一指标衡量。理想状态下，我们希望模型不仅能做出准确预测，还能“像人一样思考并表达”。只要其推理路径符合人类常识与思维模式，我们就倾向于认为该模型具备良好的可解释性。

（二）可解释性的分类体系

1. 内在可解释 vs. 事后可解释

内在可解释性（Intrinsic Interpretability）指模型自身结构简单透明，使用者可以直接观察其运作机制，如线性模型中的系数或决策树的分支路径。这类模型在设计之初就兼顾了解释能力。

事后可解释性（Post-hoc Interpretability）则是在模型训练完成后，通过额外工具或方法来解析其行为，挖掘隐藏在复杂结构中的信息，适用于神经网络等黑盒模型。

2. 局部解释 vs. 全局解释

根据应用场景的不同，解释需求可分为两类：

局部解释关注单个样本或少量样本的预测变化情况，回答“为什么这个特定输入得到这样的输出”，有助于诊断个体异常或偏差。

全局解释则试图揭示整个模型的行为规律，说明各特征如何整体影响预测结果，可用于发现数据中的普遍趋势或统计特性。

（三）当前主要研究方向概述

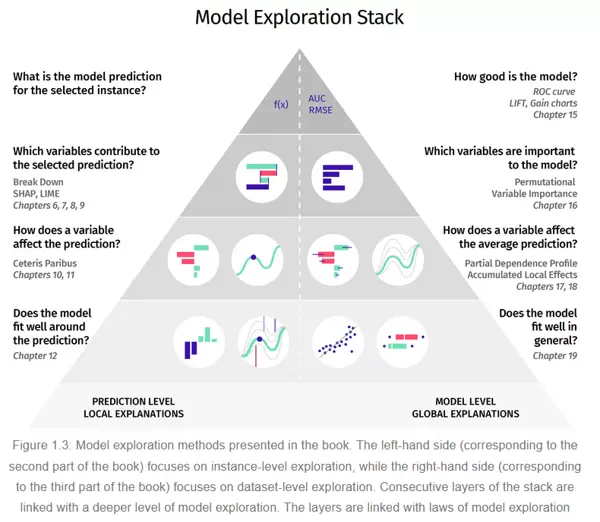
目前，在机器学习模型的发展图谱中，模型通常面临精度与可解释性之间的权衡。如下图所示，传统模型如线性回归、决策树虽然结构透明、易于理解，但在处理复杂问题时往往精度不足；而神经网络、支持向量机等高性能模型虽预测能力强，却缺乏天然的解释能力。

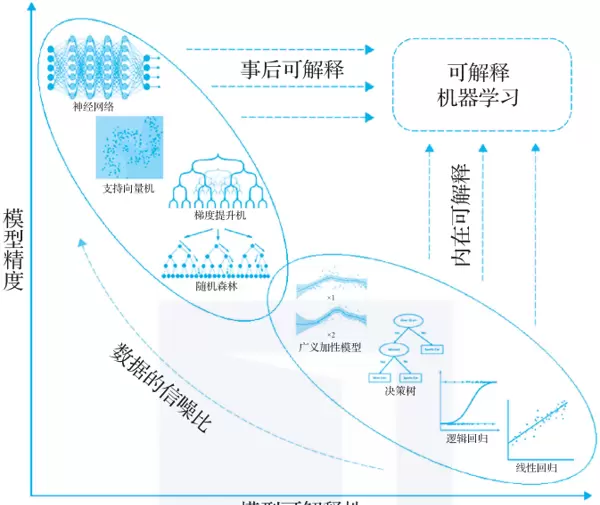
基于此矛盾，可解释机器学习主要朝两个方向发展：

方向一：增强传统模型的表达能力，保持可解释性的同时提升精度

针对逻辑回归、决策树等本身具备良好可解释性的模型，研究者尝试在不破坏其透明结构的前提下，增强其拟合能力。例如，保留加法结构但引入非线性项，从而实现更灵活的数据拟合。GAMI-Net 和 EBM（Explainable Boosting Machine）便是此类“内在可解释模型”的代表。

方向二：为复杂模型提供事后解释工具，兼顾高精度与可理解性

面对深度神经网络等高精度但难解释的模型，有两种改进思路：

• 简化模型结构（如限制树的深度），以牺牲部分性能换取更高的可读性；
• 维持原有模型结构和精度不变，在训练后使用归因分析、可视化等技术进行事后解读。

无论哪种方式，目标都是推动模型在可解释性维度上取得进步，使其更接近横轴正向的理想状态。

本文重点聚焦于第二种路径，即利用事后方法提升模型可解释性。我们将结合

sklearn

所提供的接口及示例数据集，介绍几种经典且实用的技术，包括：部分依赖图（PDP）、个体条件期望图（ICE）、置换特征重要性检验等。这些方法操作简便，适用范围广，能满足大多数模型的事后解释需求。

二、部分依赖图（Partial Dependence Plots, PDP）

“部分依赖图”（Partial Dependence Plot，简称PDP）是一种常用于机器学习模型解释与可解释性分析的技术。其核心作用是展示某个特定输入特征对模型预测结果的独立影响，同时将其他所有特征的影响进行边缘化处理。在实际应用中，机器学习模型通常包含多个特征，这些特征之间可能存在复杂的非线性关系或交互效应。

PDP通过描绘目标变量随某一特征变化的趋势，帮助我们理解模型内部的决策逻辑。从直观角度理解，部分依赖可以被视为：在给定感兴趣特征的不同取值下，模型预测输出的期望响应。

在此定义中，“感兴趣的输入特征”指的是我们希望分析的关键变量，而“补充特征”则是指模型中其余未被重点关注的变量。PDP的生成过程主要包括以下三个步骤：

1. 固定其他特征：针对某一目标特征，保持其余所有特征在训练数据中的平均值或某一固定水平，仅改变该目标特征的取值。
2. 计算预测值：对于每一个目标特征的取值，使用训练好的模型计算对应的预测结果。
3. 绘制图形：将目标特征的不同取值与其对应的平均预测结果绘制成曲线或区域图，形成部分依赖图。若预测值随特征值上升而增加，则曲线呈上升趋势；若无明显关联或呈负相关，则曲线趋于平坦或下降。

通过观察PDP，我们可以获得以下几个方面的洞察：

• 特征重要性：当某特征的取值变化引起预测结果显著波动时，说明该特征对模型输出具有较强影响力。
• 特征交互效应：若某一特征的PDP曲线在另一特征不同条件下呈现形态差异，则暗示两者之间可能存在交互作用。
• 模型稳定性与敏感性：若PDP曲线平滑且波动较小，表明模型对该特征的变化相对稳健；反之，剧烈波动则可能意味着模型对该特征过度敏感。

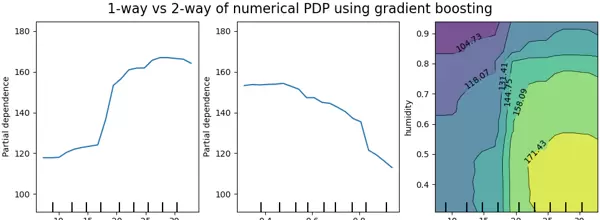
部分依赖图广泛应用于黑盒模型（如随机森林、梯度提升树、神经网络等）的解释过程中，有助于揭示模型背后的决策机制，提升模型透明度和可信度。

上图展示了基于HistGradientBoostingRegressor在共享单车数据集上构建的模型中，温度与湿度两个变量的部分依赖图（图片来源：sklearn官方教程）。其中：

单路PDP（1-way PDP）反映的是目标响应与单一输入特征之间的关系。左图显示了温度对自行车租赁数量的影响，可以看出，随着温度升高，租赁需求总体呈上升趋势。中间图为湿度的影响，显示出在中等湿度范围内租赁量较高，而在极端湿度条件下有所下降。这类分析是在忽略其他特征交互的前提下进行的，因此属于边缘效应分析。

双路PDP（2-way PDP）则进一步揭示两个特征之间的联合影响。例如右图展示了温度与湿度共同作用下的租赁数量变化模式。可以观察到明显的交互现象：当温度高于20摄氏度时，租赁数量主要受湿度影响；而在低温环境下，温度和湿度均对租赁行为产生显著影响。

sklearn.inspection

sklearn提供了专门的函数接口来生成1-way和2-way PDP，便于用户快速实现模型解释功能。

from_estimator

接下来通过一个具体案例演示PDP的实际应用。我们将在糖尿病疾病进展数据集上使用支持向量机回归（SVR）建立预测模型，并利用PDP进行解释分析。该数据集包含了BMI、血压（BP）、性别（sex）、年龄（age）、总血清胆固醇（s1）、低密度脂蛋白（S2）、高密度脂蛋白（S3）等多个生理指标，用以预测糖尿病患者的病情进展情况（disease progression）。除性别为分类变量外，其余均为连续型变量。

首先加载数据并查看各变量间的分布关系，随后构建SVR回归模型。代码如下：

from sklearn.datasets import load_diabetes
from sklearn.svm import SVR
import pandas as pd
import numpy as np

# 加载数据
diabetes_data = load_diabetes()
X = pd.DataFrame(diabetes_data["data"])
X.columns = diabetes_data["feature_names"]
y = diabetes_data["target"]

# 构建可视化数据集并绘制pairplot
dataset_to_display = X.copy()
dataset_to_display["y"] = y
import seaborn as sns
sns.pairplot(dataset_to_display)

# 使用默认参数训练SVR模型
reg = SVR().fit(X, y)
    

我们首先通过 1-way PDP 来分析各个自变量对响应变量的影响程度。以下是实现代码：

from sklearn.inspection import PartialDependenceDisplay
import matplotlib.pyplot as plt

features_interest_1way = np.arange(X.shape[1])
PartialDependenceDisplay.from_estimator(reg, X,
                                        features=features_interest_1way,
                                        grid_resolution=10)
plt.show()

从生成的图形可以观察到，某些特征如 BMI、BP（血压）、S3（总胆固醇/HDL）以及 S5（血清甘油三酯水平可能对数）对糖尿病疾病进展的预测具有较明显的影响，表现为曲线波动更为显著，说明这些变量在模型中的贡献度相对更高。

接下来，为了进一步探究特征之间的交互效应，我们构建 2-way PDP 图来可视化两个特征联合变化时对预测结果的共同影响。由于原始特征维度较高，这里仅选取部分关键特征进行组合分析：

from sklearn.inspection import PartialDependenceDisplay
import matplotlib.pyplot as plt

interest_feature_index = [2, 3, 6, 7, 8]
features_interest_2way = []

for i in range(5):
    for j in range(i + 1, 5):
        features_interest_2way.append((interest_feature_index[i], interest_feature_index[j]))

PartialDependenceDisplay.from_estimator(reg, X,
                                        features=features_interest_2way,
                                        grid_resolution=10)
plt.show()

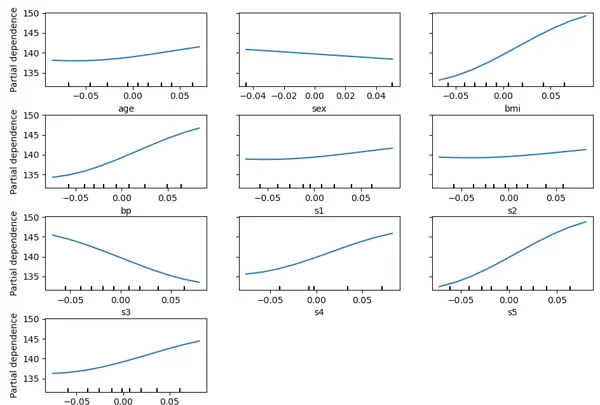
该图展示了如 BMI 与 BP、S1 等特征之间可能存在的协同作用。可以看出，在某些特征组合下，响应变量的变化趋势并非简单的线性叠加，而是呈现出更复杂的非线性关系，反映出特征间存在一定的相互影响。

个体条件期望图（Individual Conditional Expectation Plot, ICE）

ICE 图与 PDP 类似，用于揭示目标输出与某一输入特征之间的依赖关系。不同之处在于：PDP 展示的是模型预测关于某特征的平均边际效应，而 ICE 图则为每个样本单独绘制一条曲线，展现个体层面的预测行为变化。

需要注意的是，每张 ICE 图只能针对一个感兴趣的特征进行可视化。以下是以糖尿病数据集为基础，使用支持向量回归模型（SVR）所绘制的结果示例（参考 sklearn 官方文档风格）：

from sklearn.datasets import load_diabetes
from sklearn.svm import SVR
from sklearn.inspection import PartialDependenceDisplay
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

diabetes_data = load_diabetes()
X = pd.DataFrame(diabetes_data["data"][:, 0:5])
X.columns = diabetes_data["feature_names"][0:5]

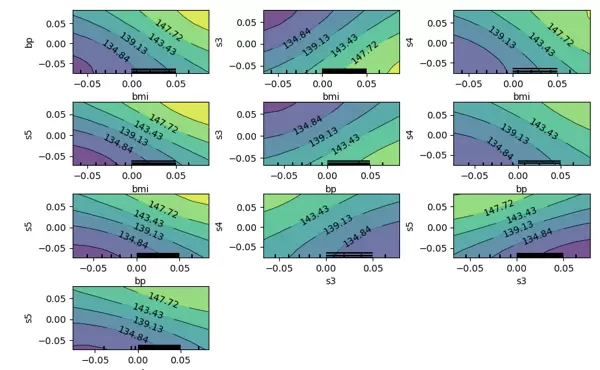
图中每条细蓝线代表一个样本在特定特征变化下的预测轨迹。尽管 PDP 能有效展示整体趋势，但其平均化过程可能会掩盖局部异质性。而 ICE 图能够揭示这种差异。例如，在温度或类似连续特征上，部分样本表现出强烈的敏感性（曲线陡峭），而另一些样本则几乎无反应（曲线平坦），这表明模型对不同人群可能存在差异化预测机制。

对于湿度这一变量，当其值超过 80% 时，部分样本的预测结果出现明显下降趋势，显示出潜在的非一致响应模式。

值得一提的是，sklearn.inspection 模块中的 PartialDependenceDisplay 函数不仅支持生成 PDP 图，也能用于绘制 ICE 图。只需设置相应参数即可实现切换：

sklearn.inspection

通过设定参数

PartialDependenceDisplay.from_estimator

可启用 ICE 模式；若进一步配置

kind='individual'

还能对图像进行中心化处理，使得各条样本曲线围绕基准点展开，便于观察偏离趋势和群体内变异性。

centered=True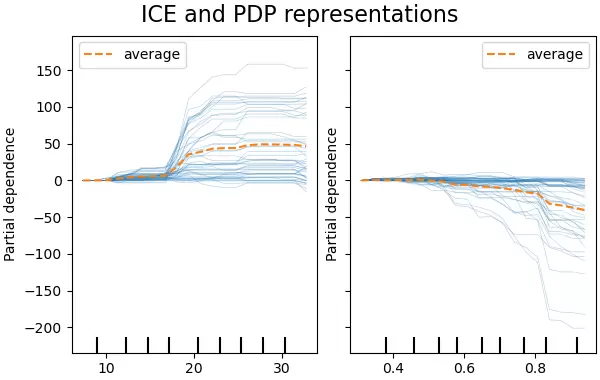

y = diabetes_data["target"] # 获取数据集中的响应变量y
reg = SVR().fit(X, y)
features_interest_1way = np.arange(X.shape[1])
PartialDependenceDisplay.from_estimator(reg, X,
                          features=features_interest_1way,
                          kind='both', # 同时绘制PDP图和ICE图，以便观察。
                          centered=True, # 按x轴第一个点的数值进行中心化处理。
                          grid_resolution=10)
plt.show()

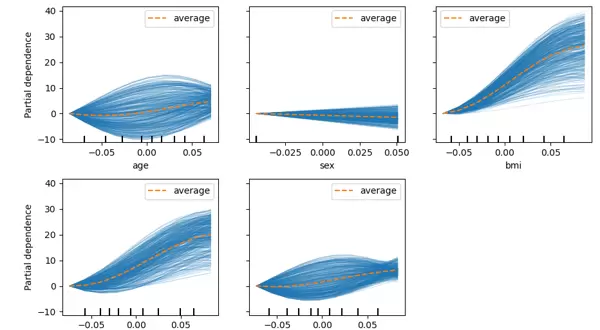
PDP图可视作所有ICE曲线的均值表现。从上图可以看出，BMI、BP、S1等多个因素对糖尿病的发展进程具有显著影响。然而，S1特征（血清胆固醇）的ICE图揭示了更丰富的信息：部分样本的ICE曲线随着S1上升先升高后下降，而另一些则呈现相反趋势——先下降再上升，显示出个体间的异质性反应。

四、置换特征重要性（Permutation Feature Importance）分析

置换特征重要性是一种用于评估模型中各特征贡献度的技术，能够衡量每个特征对模型在特定数据集上性能的影响程度。该方法尤其适用于黑箱模型，其核心思想是：随机打乱某一特征的取值，破坏其与目标变量之间的关联，然后观察模型整体性能的变化。若打乱后模型性能明显下降，则说明该特征对预测结果至关重要。

下图展示了特征置换前后对模型性能的影响（图片源自sklearn官方教程）：

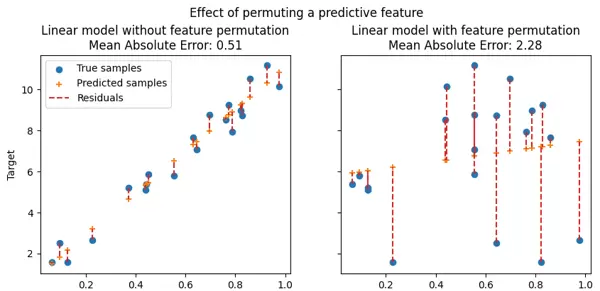
图中横轴表示特征值，纵轴为对应的目标变量（Y）取值。左侧为原始数据，右侧为某特征被随机置换后的分布情况。对于具备预测能力的特征（上方两图），置换操作打破了原有的相关结构，导致模型误差显著增加（如平均绝对误差上升）。而对于无预测力的特征（下方两图），置换后模型性能基本保持不变。

该方法的一大优势在于其“模型无关性”（model-agnostic），即可应用于任何已训练好的模型。此外，通过多次重复置换过程，可以计算特征重要性得分的方差，从而提供对估计稳定性的度量。

如下图所示，使用随机森林对泰坦尼克号幸存者数据集建模，并人为引入两个不含任何有效信息的随机特征：

random_cat

random_num

结果显示，性别、乘客等级、年龄等特征具有较高的置换重要性，而两个随机生成的特征：

random_cat

random_num

其置换重要性接近于零，符合预期。（图片来自sklearn官方教程）

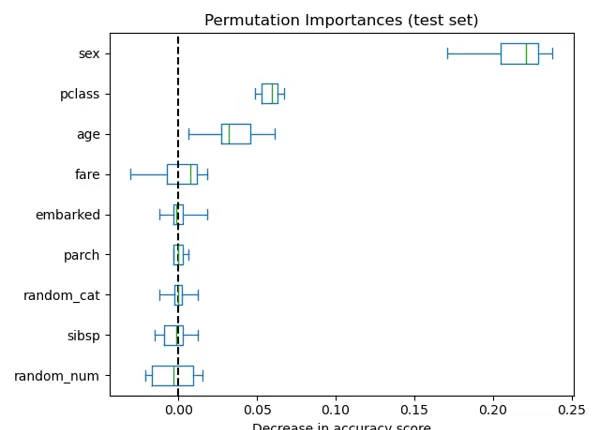
接下来以糖尿病数据集为例进行实际操作。首先加载数据并构建支持向量回归（SVR）模型：

from sklearn.datasets import load_diabetes
from sklearn.svm import SVR
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

diabetes_data = load_diabetes() # 加载数据集
X = pd.DataFrame(diabetes_data["data"]) # 获取自变量X
X.columns = diabetes_data["feature_names"] # 设置特征名称
y = diabetes_data["target"] # 获取响应变量y
reg = SVR().fit(X, y)
reg.score(X,y) # 输出0.2071777370990262

随后利用sklearn提供的工具进行置换特征重要性检验。需传入训练好的模型、输入数据及重复次数，也可通过指定参数选择不同的评估指标：

permutation_importance

scoring

from sklearn.inspection import permutation_importance
r = permutation_importance(reg, X, y,
                    n_repeats=30,
                    random_state=0,
                    scoring="r2")

for i in r.importances_mean.argsort()[::-1]:
    if r.importances_mean[i] - 2 * r.importances_std[i] > 0:
        print(f"{X.columns[i]:<8}"
              f"{r.importances_mean[i]:.3f}")

五、参考文献与拓展阅读

以下为本文涉及的主要参考资料和延伸学习资源：

核心参考文档（sklearn官方）：

• Partial Dependence Plots 相关说明：https://scikit-learn.org/stable/modules/partial_dependence.html#partial-dependence-plots
• PartialDependenceDisplay 模块使用文档：https://scikit-learn.org/stable/modules/generated/sklearn.inspection.PartialDependenceDisplay.html#sklearn.inspection.PartialDependenceDisplay.from_estimator
• 置换特征重要性示例：https://scikit-learn.org/stable/auto_examples/inspection/plot_permutation_importance.html
• Permutation Importance 官方解释：https://scikit-learn.org/stable/modules/permutation_importance.html

中文优质解读文章：

• 可解释机器学习(Explainable ML)总结 - 酒仙桥大鲨鱼的文章 - 知乎
• 终于有人把可解释机器学习讲明白了
• 偏回归图与偏残差图 - vacleon的文章 - 知乎
• Partial Dependence Plots —— 部分依赖图 - 冰焰虫子的文章 - 知乎
• 机器学习模型可解释性进行到底 ——PDP&ICE图（三） - 悟乙己的文章 - 知乎
• 机器学习模型可解释性进行到底——特征重要性（四） - 悟乙己的文章 - 知乎
• R语言可解释性机器学习（五）部分依赖图（PDP） - 修身立道的文章 - 知乎

推荐教材：

《Explainable Artificial Intelligence：An Introduction to Interpretable Machine Learning》一书中的第3.7章“Traditional Interpretable Algorithms”（第102页）对传统可解释算法进行了系统梳理，适合作为理论基础深入学习。

实用工具包（R & Python）：

DALEX 是一个广泛应用于模型解释的 R 和 Python 工具包，其设计清晰且支持多种可视化方法。该模块拥有配套的官方教材，并在官网提供了丰富的教学资源。

此外，在 DALEX 官方网站上还可以找到多个视频研讨会的录像资料，例如 useR! 2020 大会的主题演讲：“Talk with your model!”，有助于更直观地理解如何与模型进行交互式对话。

置换特征重要性的可视化处理

为了更好地展示置换特征重要性的结果，可以借助 pandas 对数据进行整理并排序：

# 利用pandas的dataframe对置换特征重要性检测结果进行一些预处理和排序
import pandas as pd
rdf = pd.DataFrame(r.importances)
rdf.index = X.columns
rdf["mean"] = r.importances_mean
rdf = rdf.sort_values(by="mean",ascending=False)
rdf = rdf.T
rdf = rdf.drop("mean",axis=0)

随后通过 seaborn 绘制箱线图以实现可视化：

# 之后，使用seaborn进行数据可视化
import seaborn as sns
sns.boxplot(rdf,orient="h")
plt.plot([0,0],[-1,rdf.shape[1]],color="#222",linestyle="--")
plt.xlabel("Decrease in accuracy score")
plt.title("permutation importances")
plt.show()

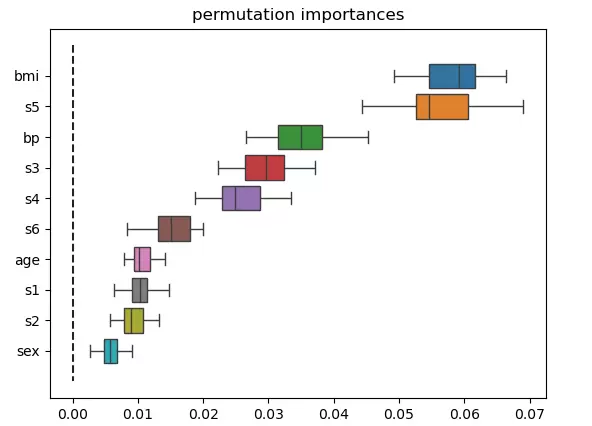
上述代码将生成如下图形结果，用于清晰呈现各特征在模型预测中的相对重要程度。

关于置换重要性的注意事项

需要特别指出的是，某些特征在表现较差的模型中可能显示出较低的重要性（即交叉验证得分低），但在性能优良的模型中却可能发挥关键作用。因此，在分析特征重要性之前，必须首先通过交叉验证等方式评估模型的整体预测能力。

置换重要性反映的并非特征本身固有的预测能力，而是该特征对特定模型预测效果的影响程度。换言之，它衡量的是当某个特征被随机打乱后，模型性能下降的程度。

结果输出格式示例

在实际计算过程中，常使用如下语句输出每个特征的重要性均值及其标准差：

f" +/- {r.importances_std[i]:.3f}"

bmi     0.058 +/- 0.005
s5      0.056 +/- 0.006
bp      0.035 +/- 0.004
s3      0.030 +/- 0.004
s4      0.026 +/- 0.004
s6      0.015 +/- 0.003
age     0.011 +/- 0.002
s1      0.010 +/- 0.002
s2      0.009 +/- 0.002
sex     0.006 +/- 0.002

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

分享0 收藏0 回帖

关键词：机器学习 解释性 Permutation conditional Progression