Optuna-模型调参

是 否 +2 论坛币

k人 参与回答

经管之家送您一份

应届毕业生专属福利!

求职就业群

赵安豆老师微信：zhaoandou666

经管之家联合CDA

送您一个全额奖学金名额~ !

立即领取

感谢您参与论坛问题回答

经管之家送您两个论坛币！

+2 论坛币

Optuna 的核心架构由多个关键组件构成，这些组件协同工作以实现高效的超参数优化。主要包含以下四个部分：

Trial（试验）：表示目标函数的一次执行实例。每一次 Trial 都会从参数空间中选取一组具体的参数值进行评估，并返回对应的目标值。在量化策略优化场景中，一次 Trial 可以理解为使用特定参数组合完成一次完整的回测流程。

Study（研究）：代表一个完整的优化任务，是多个 Trial 的集合体。它负责统筹整个优化过程，包括参数的采样调度、试验结果的记录以及最优解的追踪与管理。可以将 Study 类比为一个实验项目，保存了所有试验的历史信息和优化轨迹。

Sampler（采样器）：其职责是从预定义的参数搜索空间中生成新的参数组合。Optuna 内置多种采样算法，如 TPE（Tree-structured Parzen Estimator）、CMA-ES 和随机搜索等。其中默认的 TPE 方法能够基于历史试验的表现动态调整采样策略，在探索未知区域和利用已有优质参数之间实现良好平衡。

Pruner（剪枝器）：用于在试验过程中识别并提前终止那些表现明显落后的 Trial，从而节省计算资源。例如，在回测初期若发现某组参数导致收益极低或风险过高，Pruner 可立即中断该试验，避免无意义的后续计算。

安装与基础使用方法

首先需要安装 Optuna 及其常用依赖库，可通过 pip 命令完成：

pip install optuna xgboost pandas numpy matplotlib plotly

接下来通过一个简单示例展示 Optuna 的基本使用流程：

import optuna

# 定义目标函数
def objective(trial):
    x = trial.suggest_float('x', -10, 10)
    return (x - 2) ** 2

# 创建Study对象
study = optuna.create_study()
# 运行优化
study.optimize(objective, n_trials=100)

# 输出最优结果
print(f"最优参数: {study.best_params}")
print(f"最优值: {study.best_value}")

在此例中，我们设定目标是最小化表达式 (x2)。通过 suggest_float 方法在区间 [-10, 10] 内搜索最优参数 x。经过 100 次试验后，Optuna 成功定位到接近理论最优值的结果。

框架构建流程

数据准备与特征工程

构建量化模型的第一步是数据收集与处理。我们需要获取股票的历史行情数据及基本面信息，并据此构造有效的输入特征。以下是一个简化的数据生成流程：

import pandas as pd
import numpy as np
from datetime import datetime, timedelta

# 修复后的股票数据生成函数
def generate_stock_data(stock_code, start_date, end_date):
    dates = pd.date_range(start=start_date, end=end_date, freq='D')
    np.random.seed(42)
    
    base_price = 100
    prices = [base_price]
    for i in range(1, len(dates)):
        trend = 0.0001
        volatility = np.random.normal(0, 0.01)
        new_price = prices[-1] * (1 + trend + volatility)
        new_price = max(new_price, 1)  # 防止价格过低
        prices.append(new_price)
    
    df = pd.DataFrame({
        'date': dates,
        'open': np.array(prices) * np.random.uniform(0.99, 1.01, len(dates)),
        'high': np.array(prices) * np.random.uniform(1.0, 1.02, len(dates)),
        'low': np.array(prices) * np.random.uniform(0.98, 1.0, len(dates)),
        'close': prices,
        'volume': np.random.randint(100000, 500000, len(dates))
    })
    df['stock_code'] = stock_code
    return df

# 获取多只股票的数据（调整时间范围）
stocks_data = []
for code in ['000001.SZ', '600000.SH', '600519.SH']:

# 合并所有股票数据并按日期排序
all_stocks = pd.concat(stocks_data)
all_stocks = all_stocks.sort_values(['stock_code', 'date']).reset_index(drop=True)

# 缩短时间范围以生成个股历史行情
df = generate_stock_data(code, '2020-01-01', '2023-12-31')
stocks_data.append(df)



def calculate_technical_indicators(df):
    """计算技术指标 - 修复版本"""
    df = df.copy()

    def calculate_for_group(group):
        group = group.copy()
        group = group.sort_values('date').reset_index(drop=True)

        # 移动平均线计算（5日、20日、60日）
        group['ma_5'] = group['close'].rolling(window=5, min_periods=1).mean()
        group['ma_20'] = group['close'].rolling(window=20, min_periods=1).mean()
        group['ma_60'] = group['close'].rolling(window=60, min_periods=1).mean()

        # 收益率特征构建
        group['return_1d'] = group['close'].pct_change()
        group['return_5d'] = group['close'].pct_change(periods=5)
        group['return_20d'] = group['close'].pct_change(periods=20)

        # 历史波动率（基于20天收益率标准差）
        group['volatility_20d'] = group['return_1d'].rolling(window=20, min_periods=1).std()

        # 成交量移动平均与相对比率
        group['volume_ma_20'] = group['volume'].rolling(window=20, min_periods=1).mean()
        group['volume_ratio'] = group['volume'] / group['volume_ma_20']

        # RSI 指标计算（默认周期14）
        def calculate_rsi(data, window=14):
            delta = data.diff()
            gain = (delta.where(delta > 0, 0)).rolling(window=window, min_periods=1).mean()
            loss = (-delta.where(delta < 0, 0)).rolling(window=window, min_periods=1).mean()
            rs = gain / loss
            rsi = 100 - (100 / (1 + rs))
            return rsi

        group['rsi_14'] = calculate_rsi(group['close'])

        # MACD 指标系列计算
        group['ema_12'] = group['close'].ewm(span=12, adjust=False).mean()
        group['ema_26'] = group['close'].ewm(span=26, adjust=False).mean()
        group['macd'] = group['ema_12'] - group['ema_26']
        group['signal_line'] = group['macd'].ewm(span=9, adjust=False).mean()
        group['macd_histogram'] = group['macd'] - group['signal_line']

        return group

    # 对每只股票分组计算技术指标
    result_df = df.groupby('stock_code').apply(calculate_for_group).reset_index(drop=True)

    # 处理数值异常：将无穷大替换为缺失值
    numeric_columns = result_df.select_dtypes(include=[np.number]).columns
    result_df[numeric_columns] = result_df[numeric_columns].replace([np.inf, -np.inf], np.nan)

    return result_df

清理数据中...

移除包含缺失值（NaN）的记录行：

all_stocks_with_indicators = all_stocks_with_indicators.dropna()

输出清理后的数据维度信息：

print(f"清理后数据形状: {all_stocks_with_indicators.shape}")

展示数据覆盖的时间区间：

print(f"数据时间范围: {all_stocks_with_indicators['date'].min()} 到 {all_stocks_with_indicators['date'].max()}")

计算技术指标进度提示：

print("正在计算技术指标...")

调用函数为所有股票数据添加技术指标：

all_stocks_with_indicators = calculate_technical_indicators(all_stocks)

目标函数的设计与实现

在量化交易策略开发过程中，目标函数承担着核心作用，主要职责包括：

• 设定XGBoost模型的超参数搜索范围
• 基于当前参数组合训练预测模型
• 执行策略回测并生成绩效评估结果
• 返回用于优化的目标数值

以下为重构后的完整目标函数示例，融合了多因子选股策略的关键逻辑：

def objective(trial):
    try:
        # 定义模型参数空间 - 使用trial建议不同类型的参数值
        params = {
            'objective': 'binary:logistic',
            'eval_metric': 'auc',
            'booster': trial.suggest_categorical('booster', ['gbtree', 'gblinear', 'dart']),
            'n_estimators': trial.suggest_int('n_estimators', 50, 300),
            'max_depth': trial.suggest_int('max_depth', 3, 10),
            'learning_rate': trial.suggest_float('learning_rate', 0.01, 0.2, log=True),
            'subsample': trial.suggest_float('subsample', 0.6, 1.0),
            'colsample_bytree': trial.suggest_float('colsample_bytree', 0.6, 1.0),
            'reg_alpha': trial.suggest_float('reg_alpha', 1e-8, 1.0, log=True),
            'reg_lambda': trial.suggest_float('reg_lambda', 1e-8, 1.0, log=True),
            'gamma': trial.suggest_float('gamma', 0.0, 0.5),
            'min_child_weight': trial.suggest_int('min_child_weight', 1, 10),
            'random_state': 42
        }

        # 数据预处理阶段
        df_for_model = all_stocks_with_indicators.copy()

        # 指定用于建模的特征变量列表
        features = [
            'ma_5', 'ma_20', 'ma_60', 'volatility_20d', 'rsi_14',
            'macd', 'macd_histogram', 'volume_ratio', 'return_5d', 'return_20d'
        ]

        # 构造分类标签：次日收盘价是否上涨
        df_for_model['label'] = (df_for_model.groupby('stock_code')['close'].shift(-1) > df_for_model['close']).astype(int)
        df_for_model = df_for_model[df_for_model['label'].notna()]

        # 填充特征中的空值，使用各特征均值代替
        for feature in features:
            df_for_model[feature] = df_for_model[feature].fillna(df_for_model[feature].mean())

        # 按照股票代码和日期排序，准备划分训练集
        df_for_model = df_for_model.sort_values(['stock_code', 'date'])

        # 设定训练集截止日期
        train_date_cutoff = '2022-12-31'
        train_data = df_for_model[df_for_model['date'] <= train_date_cutoff]
    

# 创建 Study 对象并启动优化流程
study = optuna.create_study()

# 划分训练集与测试集
test_data = df_for_model[df_for_model['date'] > train_date_cutoff]
if len(train_data) == 0 or len(test_data) == 0:
    print(f"Trial {trial.number}: 数据划分失败")
    return 0.0

# 提取特征与标签
X_train = train_data[features].values
y_train = train_data['label'].values
X_test = test_data[features].values
y_test = test_data['label'].values

# 检查训练标签是否满足二分类条件
if len(np.unique(y_train)) < 2:
    print(f"Trial {trial.number}: 标签分布不平衡")
    return 0.0

# 构建 XGBoost 训练所需的数据矩阵
dtrain = xgb.DMatrix(X_train, label=y_train)
dtest = xgb.DMatrix(X_test, label=y_test)
evals = [(dtrain, 'train'), (dtest, 'eval')]

# 训练模型
model = xgb.train(
    params,
    dtrain,
    num_boost_round=1000,
    evals=evals,
    early_stopping_rounds=50,
    verbose_eval=False
)

# 执行预测并计算 AUC 指标
y_pred = model.predict(dtest)
auc = roc_auc_score(y_test, y_pred)

# 进行简化回测以评估策略表现
test_data_copy = test_data.copy()
test_data_copy['prediction'] = y_pred
test_data_copy['signal'] = (test_data_copy['prediction'] > 0.55).astype(int)
portfolio_returns = []

# 遍历每只股票进行信号驱动的模拟交易
for stock_code in test_data_copy['stock_code'].unique():
    stock_data = test_data_copy[test_data_copy['stock_code'] == stock_code].sort_values('date')
    position = 0  # 当前持仓状态：0 表示空仓，1 表示持有多头
    
    for i in range(len(stock_data) - 1):
        current_row = stock_data.iloc[i]
        next_row = stock_data.iloc[i+1]
        
        # 若出现买入信号且当前未持仓，则按收盘价买入并在下一日卖出
        if current_row['signal'] == 1 and position == 0:
            buy_price = current_row['close']
            sell_price = next_row['close']
            returns = (sell_price - buy_price) / buy_price
            portfolio_returns.append(returns)
            position = 1
        # 若出现卖出信号且当前已持仓，则平仓
        elif current_row['signal'] == 0 and position == 1:
            position = 0

# 计算投资组合的夏普比率
if len(portfolio_returns) > 0:
    portfolio_returns = np.array(portfolio_returns)
    sharpe_ratio = np.mean(portfolio_returns) / np.std(portfolio_returns) * np.sqrt(252) if np.std(portfolio_returns) > 0 else 0
    print(f"Trial {trial.number}: AUC={auc:.4f}, 夏普比率={sharpe_ratio:.4f}, 交易次数={len(portfolio_returns)}")
    
    # 综合评分：结合夏普比率和 AUC，赋予不同权重
    composite_score = 0.6 * sharpe_ratio + 0.4 * auc
    return composite_score
else:
    # 若无有效交易记录，仅返回 AUC 作为基础评价指标
    print(f"Trial {trial.number}: 没有交易")
    return auc

# 超参数优化配置
study = optuna.create_study(
    direction='maximize',
    sampler=optuna.samplers.TPESampler(seed=42)
)

print("开始超参数优化...")
print(f"数据总量: {len(all_stocks_with_indicators)}")

# 执行优化过程（减少试验次数以提升运行效率）
study.optimize(objective, n_trials=10, show_progress_bar=True)

# 输出最终优化结果
if len(study.trials) > 0 and study.best_value > 0:
    print("\n=== 优化完成 ===")
    print(f"最优试验编号: {study.best_trial.number}")
    print(f"最优综合评分: {study.best_value:.4f}")
    print(f"最优参数: {study.best_trial.params}")
else:
    print("\n优化未能找到有效结果，请检查数据和参数设置")

Optuna 可视化功能介绍

Optuna 内置了多种可视化工具，位于 optuna.visualization 模块中，便于分析优化过程与结果。默认使用 Plotly 作为绘图后端，支持生成交互式图表。

基础环境设置

在进行可视化之前，需先导入相关模块并配置显示参数：

import optuna.visualization as vis

# 若需支持中文显示，可设置 Matplotlib 字体
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False

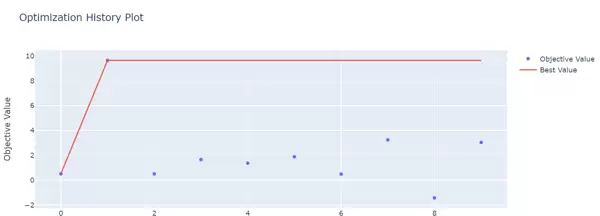
优化历史趋势图

通过 plot_optimization_history 可查看每次试验中目标函数最优值的变化趋势，判断优化是否趋于收敛：

fig = vis.plot_optimization_history(study)
fig.show()

（该图表包含多个交互控件，实际使用时可自行探索操作）

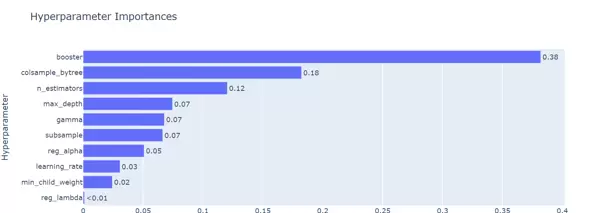
参数重要性评估

利用 plot_param_importances 可直观展示各超参数对模型性能影响的重要性排序：

fig = vis.plot_param_importances(study)
fig.show()

多维度参数关系可视化

Optuna 提供多种方式用于分析参数之间的关联性：

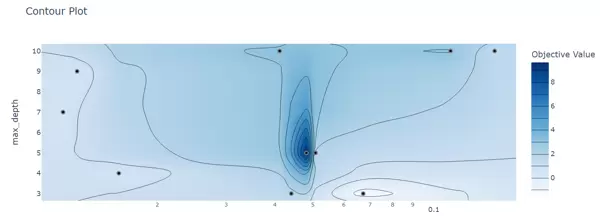
• 等高线图（Contour Plot）：使用 plot_contour 展示两个参数间的交互效应。

fig = vis.plot_contour(study, params=['max_depth', 'learning_rate'])
fig.show()

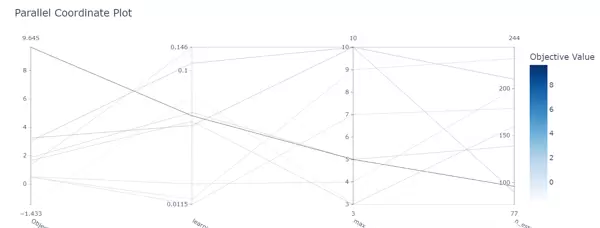
• 平行坐标图（Parallel Coordinate）：通过 plot_parallel_coordinate 分析高维参数组合下目标值的分布情况。

fig = vis.plot_parallel_coordinate(study, params=['max_depth', 'learning_rate', 'n_estimators'])
fig.show()

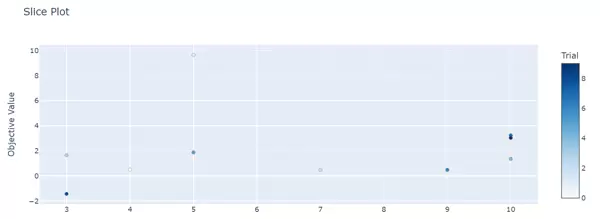
• 切片图（Slice Plot）：使用 plot_slice 观察单一参数变化对目标值的影响趋势。

fig = vis.plot_slice(study, params=['max_depth'])
fig.show()

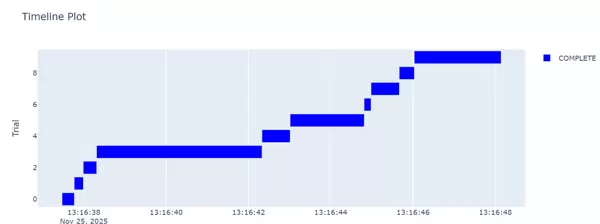
试验时间线分析

plot_timeline 可呈现每个试验的启动时间、执行时长及最终状态，有助于：

• 识别耗时异常的试验任务
• 发现失败或中断的试验记录
• 掌握整体优化过程的时间分布特征

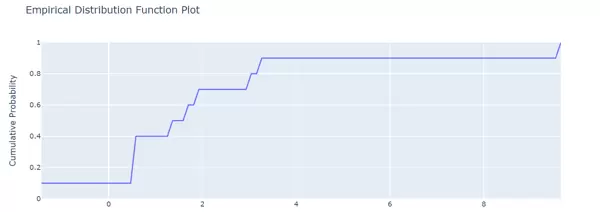
目标值经验分布函数图

通过 plot_edf 绘制目标值的经验分布函数（Empirical Distribution Function），帮助理解目标值在整个优化过程中的累积分布形态：

fig = vis.plot_edf(study)
fig.show()

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

分享0 收藏0 回帖

关键词：OPT Optimization distribution Categorical Indicators