深度学习入门实战--全连接神经网络

是 否 +2 论坛币

k人 参与回答

经管之家送您一份

应届毕业生专属福利!

求职就业群

赵安豆老师微信：zhaoandou666

经管之家联合CDA

送您一个全额奖学金名额~ !

立即领取

感谢您参与论坛问题回答

经管之家送您两个论坛币！

+2 论坛币

全连接神经网络中的常见激活函数分析

在深度学习中，激活函数是神经网络实现非线性表达能力的关键组成部分。以下将介绍几种常用的激活函数及其特性。

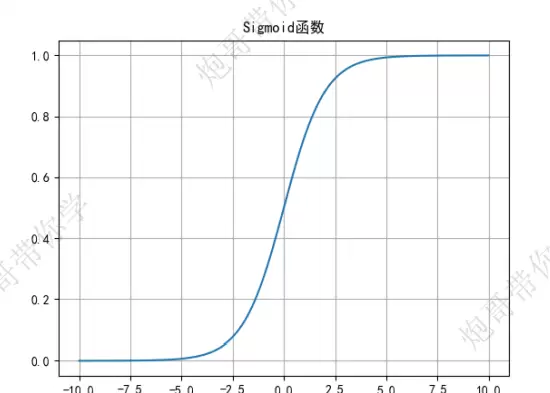
Sigmoid 函数

公式定义为：
y = 1 / (1 + e^-z)
其导数形式为：
y′ = y(1 - y)

优点：

• 结构简单，输出范围在 (0,1) 区间内，非常适合用于二分类任务的输出层。

缺点：

• 在反向传播过程中容易出现梯度消失问题，尤其是在权重初始化过小的情况下，导致梯度趋近于零，参数难以更新。
• 输出区间不关于原点对称，这会影响后续层的训练效率，因为非对称输入可能导致更新方向不稳定。
• 由于梯度更新路径可能在不同方向上波动较大，优化过程变得复杂，整体训练时间增加。

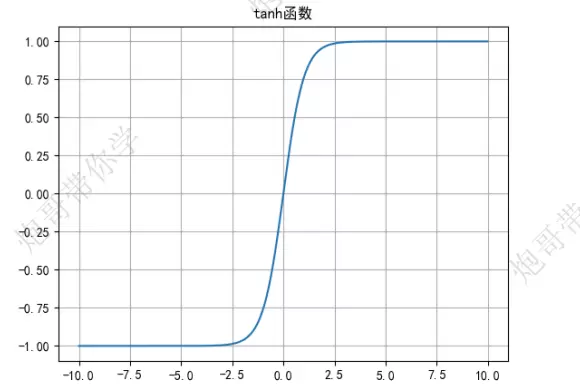
Tanh 函数

数学表达式为：
y = (e^z - e^-z) / (e^z + e^-z)
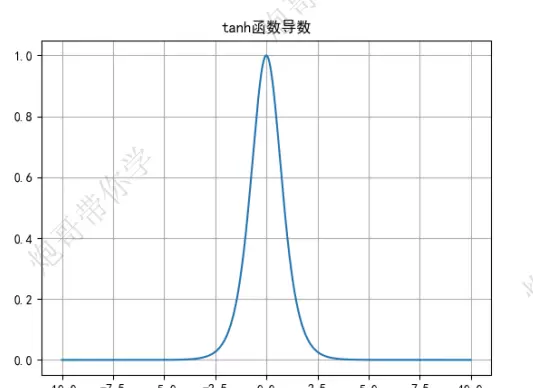
求导后得到：
y′ = 1 - y

优点：

• 相较于 Sigmoid 函数，Tanh 的输出是以 0 为中心的，即值域为 (-1, 1)，解决了非零对称的问题，有助于加快模型收敛速度。
• 最大导数值可达 1.0，远高于 Sigmoid 的 0.25，因此在梯度传递方面更具优势，训练效率更高。

缺点：

• 仍然存在梯度消失的风险，特别是在输入绝对值较大时，函数两端趋于饱和，导数接近零。
• 与 Sigmoid 函数结构相似，本质缺陷也较为接近，未能根本解决深层网络中的梯度问题。

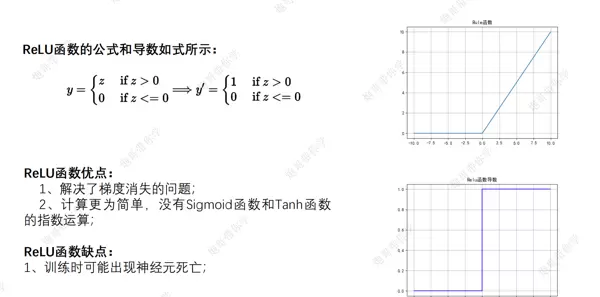
ReLU 激活函数

该函数在现代神经网络中广泛应用，具有计算高效、缓解梯度消失的优点。其图像如下所示：

Leaky ReLU 函数

作为 ReLU 的改进版本，Leaky ReLU 在负半轴引入了一个微小斜率，避免了“神经元死亡”现象。其示意图如下：

SoftMax 激活函数

SoftMax 函数的输出值位于 [0,1] 范围内，并且多个输出节点的概率总和恒等于 1。例如，在一个三分类任务中，SoftMax 会输出三个分别对应各类别的概率值，且三者之和为 1。

正因如此，SoftMax 常被用作多分类任务中神经网络最后一层的激活函数，便于进行概率解释和类别判定。

反向传播机制简介

反向传播是训练神经网络的核心算法之一，通过误差从输出层向输入层逐层回传，来调整网络中的权重和偏置参数。具体流程如下：

1. 数据输入：将样本数据送入网络进行处理。
2. 前向传播：信号逐层传递，最终得到预测输出结果。
3. 计算损失：利用损失函数衡量预测值与真实标签之间的误差。
4. 梯度计算：根据损失函数对各层的权重 W 和偏置 b 分别求偏导，获得梯度信息。
5. 参数更新：沿梯度反方向调整 W 和 b 的值，完成一次迭代优化。随后重复上述步骤直至模型收敛。

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

分享0 收藏0 回帖

关键词：神经网络 深度学习 神经网 数学表达式 激活函数