Exhibit 8.1 AR(1) 模型拟合与残差可视化(color 数据集) 加载时间序列分析专用包 TSA,并读取其中的 color 内置数据集。该数据集可能记录了与颜色相关的时序观测值。 使用 arima() 函数对 color 序列拟合一个 AR(1) 模型(即自回归阶数为1,无差分、无移动平均项),并将结果保存为 m1.color。随后输出模型估计结果,包括系数、标准误及对数似然等统计量。为进一步评估模型拟合效果,绘制标准化残差的时间序列图。通过 rstandard() 提取标准化残差,以 'o' 类型绘制点线结合图形,纵轴标注为“Standardized residuals”。同时添加一条 y=0 的水平参考线,便于观察残差是否围绕零值随机波动。
Exhibit 8.2 AR 模型优化(hare 数据集) 载入 hare 数据集,该数据包含野兔种群数量随时间变化的观测值。为改善序列的平稳性,先对原始数据进行平方根变换,再拟合一个 AR(3) 模型。 初步模型结果显示,AR(2) 项的系数不显著,提示可考虑将其剔除或设为零。因此构建第二个模型 m2.hare,在 arima() 中利用 fixed 参数将 AR(2) 系数固定为 0,其余参数自由估计。
重新拟合并输出新模型结果,可见参数精简后模型更简洁且有效。
接着绘制优化后模型 m2.hare 的标准化残差序列图,依然采用 type='o' 显示趋势,并加入 h=0 的横线辅助判断残差是否存在系统性偏差。
Exhibit 8.3 IMA (1,1) 模型拟合(oil.price 数据集) 导入 oil.price 数据集,代表油价的历史变动情况。首先对数据取自然对数,以稳定方差并增强线性结构。 计算并绘制对数变换后序列的自相关函数(ACF)图像,用于识别潜在的依赖结构。
同时绘制偏自相关函数(PACF)图,帮助判断自回归部分的阶数。
基于 ACF 和 PACF 的特征,选择建立 IMA(1,1) 模型,即 ARIMA(0,1,1) 模型。具体操作是对 log(oil.price) 进行一次差分处理,并引入一阶移动平均项,调用 arima(log(oil.price), order=c(0,1,1)) 实现建模。 完成拟合后,绘制该模型的标准化残差,使用 type='l' 表示连续线条形式呈现,同样添加 y=0 参考线。
进一步开展残差异常值的概率分析:计算标准正态分布下 |Z| > 3 的概率 p,约为 0.00135;然后基于二项分布计算在 241 个残差中出现至少 4 个极端值的概率,以此检验异常点是否超出预期。
Exhibit 8.4 残差正态性检验 为了验证模型残差是否符合正态假设,首先绘制 Q-Q 图。使用 qqnorm() 绘制 m1.color 模型残差的分位点,并设置点型为实心圆(pch=20)、颜色为红色(col=2),大小适当缩小(cex=0.8)。再通过 qqline() 添加理论正态分布的参考直线,颜色设为蓝色(col=4),直观判断偏离程度。
接下来执行 Shapiro-Wilk 正态性检验,调用 shapiro.test() 对同一模型的残差进行统计推断,获得检验统计量和 p 值,以量化方式评估正态性假设是否成立。
此外,还尝试 Kolmogorov-Smirnov 检验(K-S 检验),由于原始残差可能存在重复值,影响检验有效性,故使用 jitter() 对数据轻微扰动以避免问题。调用 ks.test() 并指定比较分布为正态分布 pnorm,需填入样本均值和标准差(原文省略具体数值)。 Exhibit 8.8 AR(1) 模型系数的置信区间计算 设定滞后阶数 k 从 1 到 20,提取 m1.color 模型中的自回归系数 φ(phi),以及 color 数据的长度 n。 利用解析公式 sqrt((1 - (1 - φ) × φ^(2k2)) / n) 计算每个滞后阶数下 φ^k 的渐近标准差,作为构造置信区间的依据。通过 lapply 遍历所有 k 值并返回结果列表。
Exhibits 8.9–8.10:残差自相关性检验(ACF 图) 绘制 m1.color 模型残差的样本自相关函数图(ACF),主标题设为“残差的样本自相关函数”,检查是否存在显著的剩余相关性。
Exhibit 8.11:Ljung-Box Q 检验(定量检验残差自相关) 为实现 Ljung-Box 检验做准备,首先调用 acf(residuals(m1.color), plot=F) 获取残差的 ACF 数值而不绘图,提取其 acf 属性值。
从中截取前六个自相关系数,并使用 signif() 函数保留两位有效数字,便于后续参与 Q 统计量计算或报告展示。
计算 Ljung-Box Q 统计量的过程如下:
首先确定数据长度,使用命令获取序列 color 的长度:
n = length(color)
接着根据 Ljung-Box Q 统计量的公式进行计算:
Q = n * (n + 2) * sum(a^2 / ((n - 1) : (n - length(a))))
该公式用于检验残差是否为白噪声。计算完成后输出 Q 值:
Q
然后进一步计算对应的 p 值,采用卡方分布函数:
1 - pchisq(Q, 5)
其中自由度取值为 5,对应滞后阶数减去模型参数个数(例如 6 - 1)。结果可用于判断是否存在显著自相关。

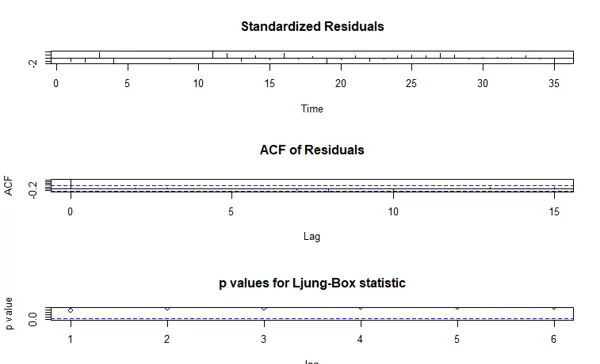
接下来生成综合残差诊断图(tsdiag),以便对模型残差进行全面评估:
tsdiag(m1.color, gof = 6, omit.initial = F)
此图包含标准化残差、自相关函数图以及 p 值序列,帮助判断模型拟合效果和残差的随机性。
以下是对 color 数据集的不同 ARIMA 模型进行比较的部分内容:
首先是已经拟合好的 AR(1) 模型,其结果可作为基准用于后续对比:
m1.color

随后构建其他几种时间序列模型以作比较:
拟合一个 AR(2) 模型,增加自回归部分的阶数:
m2.color = arima(color, order = c(2, 0, 0))
建立 ARMA(1,1) 模型,同时考虑一阶自回归与一阶移动平均项:
m3.color = arima(color, order = c(1, 0, 1))
进一步尝试更复杂的 ARMA(2,1) 模型:
m4.color = arima(color, order = c(2, 0, 1))
这些模型可用于分析不同结构在拟合精度和残差特性上的差异。
此外,针对 hare 数据集的平方根序列,拟合了一个 AR(3) 模型,并对其残差执行游程检验(runs test)以检测随机性:
m1.hare = arima(sqrt(hare), order = c(3, 0, 0))
运行游程检验命令:
runs(residuals(m1.hare), k = 0)
该检验有助于判断残差序列中是否存在系统性偏离随机模式的现象。





 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







