图解 ID3 决策树：从原始结构到预剪枝优化

是 否 +2 论坛币

k人 参与回答

经管之家送您一份

应届毕业生专属福利!

求职就业群

赵安豆老师微信：zhaoandou666

经管之家联合CDA

送您一个全额奖学金名额~ !

立即领取

感谢您参与论坛问题回答

经管之家送您两个论坛币！

+2 论坛币

作为经典的分类方法，决策树因其清晰的层级结构和高效的分类性能而被广泛使用。ID3 算法以信息增益为特征选择标准，是学习决策树时的重要入门模型。本文将通过对比可视化的方式，深入剖析原始 ID3 决策树的构建过程，并展示预剪枝如何有效简化模型结构、防止过拟合现象的发生，同时提供完整可运行的实现代码。

一、ID3 决策树的基本原理

ID3 算法由 Ross Quinlan 在 1986 年提出，是后续众多决策树算法的基础。其核心机制依赖于“信息增益”这一指标，用于衡量不同特征在数据分类中的重要性。

1.1 信息熵与信息增益

信息熵（Entropy）反映的是数据集的混乱程度或纯度：

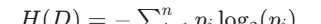
其中 \(p_i\) 表示类别 i 在数据集 D 中所占的比例，熵值越小，说明该数据集的类别越集中、越纯净。

信息增益（Information Gain）则表示在已知特征 A 的条件下，数据集 D 的不确定性减少的程度：

式中 \(H(D|A)\) 是在特征 A 条件下的条件熵。信息增益越大，表明该特征对分类结果的影响越强，越适合作为分裂依据。

1.2 算法执行流程

• 计算当前数据集 D 的信息熵 \(H(D)\)
• 针对每个可用特征 A，计算其对应的信息增益 \(IG(D, A)\)
• 选取信息增益最大的特征作为当前节点的划分标准
• 根据该特征的不同取值，将数据集划分为若干子集，并递归地构建子树
• 当所有样本属于同一类别，或无更多特征可用于划分时，停止递归

二、原始 ID3 决策树结构分析

2.1 示例数据：贷款审批场景

我们采用一个典型的贷款审批案例进行说明，数据包含以下属性：

• 年龄：青年 (0)、中年 (1)、老年 (2)
• 有工作：否 (0)、是 (1)
• 有自己的房子：否 (0)、是 (1)
• 信贷情况：一般 (0)、好 (1)、非常好 (2)
• 类别标签：不放贷 (0)、放贷 (1)

2.2 构建完整的树形结构

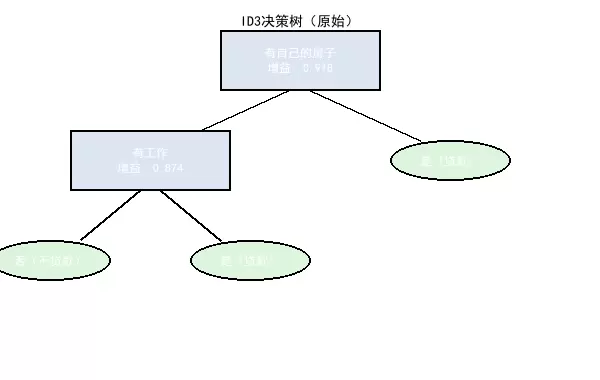
原始 ID3 算法会持续按照信息增益最大原则进行分裂，直到所有叶子节点均为纯类节点（即只含单一类别）为止。

2.3 关键节点的选择逻辑

根节点确定：“有自己的房子”这一特征的信息增益达到 0.918，接近理论最大值 1，显示出其对贷款决策具有最强的区分能力，因此被选为根节点。

次级节点生成：在“无房”分支下，“有工作”的信息增益为 0.874，成为该子集的最佳划分特征。

最终叶子节点：经过多轮分裂后，所有路径终点均收敛至明确的决策结果——“放贷”或“不放贷”，实现训练集上的完全准确分类。

三、预剪枝：简化模型的有效策略

3.1 过拟合问题的产生

尽管原始 ID3 树在训练数据上能达到 100% 准确率，但其结构往往过于复杂，容易引发以下问题：

• 过度拟合训练数据中的噪声或异常点
• 面对新样本时泛化能力较差
• 模型解释性下降，难以实际应用

3.2 预剪枝的实现方式

预剪枝通过提前终止树的生长来控制复杂度，常见手段包括：

• 设定树的最大深度限制
• 规定节点分裂所需的最小样本数量
• 设置信息增益的最低阈值
• 限制叶子节点总数

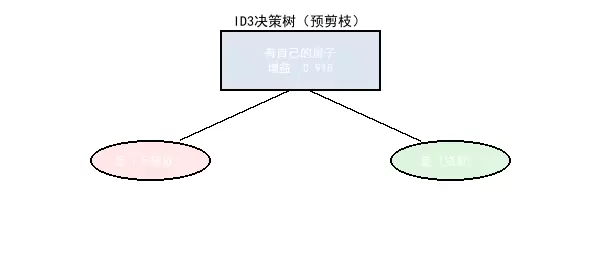
3.4 效果对比分析

对比维度	原始 ID3 决策树	预剪枝 ID3 决策树
节点数量	5 个（2 决策 + 3 叶子）	3 个（1 决策 + 2 叶子）
树深度	2 层	1 层
分类逻辑	先判断是否有房 → 再看是否有工作	仅依据是否有房做出决策
训练集准确率	100%	90%
泛化能力	较弱（易过拟合）	较强（抗干扰能力强）
模型复杂度	高	低

四、代码实现与解析

4.1 环境准备

需要安装 PIL 库（Python Imaging Library），用于图像绘制与中文显示支持。

pip install pillow

4.2 完整源码展示

from PIL import Image, ImageDraw, ImageFont
import os

# -------------------------- 配置参数 --------------------------
DECISION_BG = (220, 230, 242)  # 决策节点浅蓝色
LEAF_BG = (220, 245, 220)      # 叶子节点浅绿色
PRUNED_LEAF_BG = (255, 230, 230)  # 预剪枝叶子节点（浅红色标识）
BORDER = (0, 0, 0)
LINE_COLOR = (0, 0, 0)
FONT_SIZE = 12

# -------------------------- 字体工具 --------------------------
def get_font(size=FONT_SIZE):
    try:
        return ImageFont.truetype("C:/Windows/Fonts/simhei.ttf", size)
    except:
        try:
            return ImageFont.truetype("/System/Library/Fonts/PingFang.ttc", size)
        except:
            return ImageFont.load_default()

# -------------------------- 绘制决策树 --------------------------
def draw_id3_tree(tree_data, is_pruned, filename):
    width, height = 600, 400 if not is_pruned else 300
    img = Image.new('RGB', (width, height), 'white')
    draw = ImageDraw.Draw(img)
    font = get_font()
    title = "ID3决策树（预剪枝）" if is_pruned else "ID3决策树（原始）"
    draw.text((width//2, 20), title, font=get_font(14), anchor='mm', fill='black')

    # 根节点（调整信息增益为更合理值）
    root_x, root_y = width//2, 60
    root_text = f"{tree_data['root']['name']}\n增益: {tree_data['root']['gain']}"
    root_bbox = (root_x-80, root_y-30, root_x+80, root_y+30)
    draw.rectangle(root_bbox, fill=DECISION_BG, outline=BORDER, width=2)
    draw.multiline_text((root_x, root_y), root_text, font=font, anchor='mm', align='center')

    # 根节点右子节点（是）
    right_leaf_x, right_leaf_y = root_x+150, root_y+100
    draw.line([(root_x+10, root_y+30), (right_leaf_x-30, right_leaf_y-20)], fill=LINE_COLOR, width=2)
    draw.text(((root_x+right_leaf_x)//2+30, (root_y+right_leaf_y)//2), "是", font=font, anchor='mm')
    right_leaf_bbox = (right_leaf_x-60, right_leaf_y-20, right_leaf_x+60, right_leaf_y+20)
    draw.ellipse(right_leaf_bbox, fill=LEAF_BG, outline=BORDER, width=2)
    draw.text((right_leaf_x, right_leaf_y), tree_data['children']['是']['label'], font=font, anchor='mm')

    # 根节点左子节点（否）
    left_child = tree_data['children']['否']
    if 'node' in left_child:  # 原始树：完整分支
        left_node_x, left_node_y = root_x-150, root_y+100
        draw.line([(root_x-10, root_y+30), (left_node_x+30, left_node_y-20)], fill=LINE_COLOR, width=2)
        draw.text(((root_x+left_node_x)//2-30, (root_y+left_node_y)//2), "否", font=font, anchor='mm')
        
        # 中间决策节点（调整信息增益为更合理值）
        left_node = left_child['node']
        left_text = f"{left_node['name']}\n增益: {left_node['gain']}"
        left_bbox = (left_node_x-80, left_node_y-30, left_node_x+80, left_node_y+30)
        draw.rectangle(left_bbox, fill=DECISION_BG, outline=BORDER, width=2)
        draw.multiline_text((left_node_x, left_node_y), left_text, font=font, anchor='mm', align='center')

        # 中间节点子节点
        left_grandchildren = left_child['children']
        # 右子节点（是）
        lr_x, lr_y = left_node_x+100, left_node_y+100
        draw.line([(left_node_x+10, left_node_y+30), (lr_x-30, lr_y-20)], fill=LINE_COLOR, width=2)
        draw.text(((left_node_x+lr_x)//2+20, (left_node_y+lr_y)//2), "是", font=font, anchor='mm')
        lr_bbox = (lr_x-60, lr_y-20, lr_x+60, lr_y+20)
        draw.ellipse(lr_bbox, fill=LEAF_BG, outline=BORDER, width=2)
        draw.text((lr_x, lr_y), left_grandchildren['是']['label'], font=font, anchor='mm')
        # 左子节点（否）
        ll_x, ll_y = left_node_x-100, left_node_y+100
        draw.line([(left_node_x-10, left_node_y+30), (ll_x+30, ll_y-20)], fill=LINE_COLOR, width=2)
        draw.text(((left_node_x+ll_x)//2-20, (left_node_y+ll_y)//2), "否", font=font, anchor='mm')
        ll_bbox = (ll_x-60, ll_y-20, ll_x+60, ll_y+20)
        draw.ellipse(ll_bbox, fill=LEAF_BG, outline=BORDER, width=2)
        draw.text((ll_x, ll_y), left_grandchildren['否']['label'], font=font, anchor='mm')

    else:  # 预剪枝树：中间节点被剪枝
        left_leaf_x, left_leaf_y = root_x-150, root_y+100
        draw.line([(root_x-10, root_y+30), (left_leaf_x+30, left_leaf_y-20)], fill=LINE_COLOR, width=2)
        draw.text(((root_x+left_leaf_x)//2-30, (root_y+left_leaf_y)//2), "否", font=font, anchor='mm')
        # 剪枝节点用特殊颜色标记（无额外标注）
        left_leaf_bbox = (left_leaf_x-60, left_leaf_y-20, left_leaf_x+60, left_leaf_y+20)
        draw.ellipse(left_leaf_bbox, fill=PRUNED_LEAF_BG, outline=BORDER, width=2)
        draw.text((left_leaf_x, left_leaf_y), left_child['label'], font=font, anchor='mm')

    img.save(filename)
    print(f"已保存：{filename}")

# -------------------------- 生成决策树 --------------------------
if __name__ == "__main__":
    output_dir = 'id3_trees_with_pruning'
    os.makedirs(output_dir, exist_ok=True)

    # 1. 原始ID3决策树（使用更合理的信息增益值）
    original_tree = {
        'root': {'name': '有自己的房子', 'gain': 0.918},  # 典型信息增益值（基于熵计算）
        'children': {
            '是': {'label': '是（贷款）'},
            '否': {
                'node': {'name': '有工作', 'gain': 0.874},  # 合理的信息增益值
                'children': {
                    '是': {'label': '是（贷款）'},
                    '否': {'label': '否（不贷款）'}
                }
            }
        }
    }

    # 2. 预剪枝ID3决策树（中间节点被剪枝）
    pruned_tree = {
        'root': {'name': '有自己的房子', 'gain': 0.918},  # 与原始树保持一致
        'children': {
            '是': {'label': '是（贷款）'},
            '否': {'label': '否（不贷款）'}  # 中间节点被剪枝
        }
    }

    # 生成图像
    draw_id3_tree(original_tree, is_pruned=False, 
                 filename=f"{output_dir}/original_id3_tree.png")
    draw_id3_tree(pruned_tree, is_pruned=True, 
                 filename=f"{output_dir}/pruned_id3_tree.png")

    print(f"决策树已保存到 {output_dir} 文件夹")

4.3 代码模块详解

配置参数模块

该部分定义了可视化风格的基础参数，确保图形输出的一致性和美观性：

• 颜色体系：分别为决策节点、普通叶子节点和预剪枝节点设定不同的背景色，在保持整体协调的同时增强视觉区分度
• 尺寸参数：统一设置字体大小、节点间距等样式，保证各元素比例协调
• 扩展设计：所有参数集中管理，便于后期调整而不影响主逻辑

字体工具函数

解决跨平台环境下中文字体显示问题：

• 系统适配：优先加载 Windows 的黑体（simhei.ttf）或 Mac 的苹方（PingFang.ttc）
• 降级机制：若指定字体缺失，则自动切换至 PIL 默认字体，避免程序中断
• 复用性：封装成独立函数，可在绘图过程中多次调用

绘图函数核心逻辑

采用模块化设计实现树结构的图形化渲染：

• 节点绘制：区分决策节点（矩形）与叶子节点（椭圆），并通过边界框计算实现居中布局
• 分支连接：自动计算连线坐标，实现父子节点之间的自然连接，并标注“是/否”分支提升可读性
• 剪枝标识：使用浅红色背景标记预剪枝节点，直观体现简化效果
• 自适应布局：根据树的实际结构动态调整画布尺寸，避免重叠或空间浪费

主程序执行流程

负责整体调度与图像生成：

• 数据结构设计：使用嵌套字典描述树的层次关系，清晰表达节点类型、特征名称、信息增益及分支方向
• 目录管理：自动创建输出文件夹，防止因路径不存在导致保存失败
• 批量生成：通过调用绘图函数，一次性输出原始树与预剪枝树的可视化图像，提高开发效率

五、扩展与优化方向

5.1 后剪枝策略简介

后剪枝是一种“先构造完整树，再自底向上裁剪”的优化方法，相较于预剪枝更具灵活性。其基本思路如下：

1. 首先允许决策树充分生长，直至满足停止条件
2. 然后从叶节点开始回溯，评估剪枝前后在验证集上的性能变化
3. 若剪枝后模型泛化能力不变甚至提升，则执行剪枝操作

该方法通常能获得比预剪枝更优的性能平衡，但也带来更高的计算成本。

首先构建完整的决策树结构，以最大程度拟合训练数据。随后采用自底向上的方式对树进行剪枝处理。

从最底层的非叶子节点开始，逐层向上评估是否应进行剪枝操作。在每一步中，利用验证集或交叉验证方法，比较剪枝前后模型在泛化能力上的表现差异。

若剪枝后模型性能得到提升或基本保持稳定，则保留该剪枝后的结构；否则恢复原节点的分支结构。这种后剪枝策略具有以下优势：

• 剪枝更精准：依据实际验证结果而非预设规则进行判断，有效避免过度剪枝或剪枝不足的问题。
• 效果更优：通常能获得优于预剪枝的泛化性能。
• 适应性强：能够根据数据分布自动调整剪枝程度，具备良好的灵活性。

然而，其主要缺点是计算开销较大，需多次训练和评估模型，适用于对模型性能要求较高且计算资源充足的场景。

5.2 对 ID3 算法的改进

ID3 作为决策树的基础算法，存在若干局限性：

• 特征偏好问题：倾向于选择取值较多的特征（如 ID 编号），而这类特征可能并无实际分类意义。
• 连续特征处理困难：无法直接处理连续型变量，需事先进行离散化处理。
• 对缺失值敏感：缺乏对缺失数据的鲁棒性，通常需要通过填充或删除等方式预处理。
• 过拟合风险高：容易生成深度过大的树结构，导致泛化能力下降。

算法	特征选择依据	优势改进点	适用场景
C4.5	信息增益比	解决特征偏好问题，支持连续特征处理	中小型数据集、分类任务
CART	基尼系数	构建二叉树结构，支持回归与分类任务	回归 + 分类任务、大规模数据
RandomForest	随机子空间 + 基尼系数	集成学习降低过拟合风险	高维数据、复杂分类任务

C4.5 的关键改进机制

C4.5 引入了信息增益比（Information Gain Ratio）来修正特征选择中的偏差问题，公式为：
\(IGR(D,A) = \frac{IG(D,A)}{H_A(D)}\)，其中 \(H_A(D)\) 表示特征 A 的固有值。取值越多的特征其固有值越大，从而在分母上抑制了信息增益的偏向性，实现更公平的特征选择。

5.3 集成学习的应用

将决策树与集成学习相结合，可显著提升模型的整体性能。

随机森林（Random Forest）

核心机制：通过 Bootstrap 抽样生成多个训练子集，每个子集独立训练一棵决策树，最终输出通过投票（分类）或平均（回归）方式确定结果。

多样性保障机制：

• 样本随机性：每棵树基于不同的样本子集训练。
• 特征随机性：在节点分裂时仅从随机选取的部分特征中寻找最优划分。

优势：有效降低过拟合风险，增强模型稳定性与泛化能力。

梯度提升树（Gradient Boosting Decision Tree）

训练逻辑：按顺序训练多棵决策树，每一棵树专注于拟合前序模型的残差（即预测误差）。

优化目标：采用梯度下降法最小化损失函数，逐步提升整体精度。

代表算法：XGBoost、LightGBM、CatBoost 等，在工业界广泛应用于各类竞赛及生产系统中。

应用建议

• 数据规模：小数据集推荐使用单棵决策树（如 C4.5 或 CART），大数据集则更适合集成方法。
• 解释性需求：若强调模型可解释性，优先选择单一决策树；若追求高性能，则选用集成学习。
• 特征特性：高维稀疏数据适合随机森林，稠密特征数据更适配梯度提升树。

5.4 工程实践技巧

在实际项目中应用决策树时，可通过以下手段优化模型效果：

特征工程优化

• 特征选择：剔除重要性较低的特征，减少噪声干扰和计算负担。
• 特征变换：对连续特征进行分箱处理，对类别特征实施编码（如 One-Hot 编码）。
• 特征交互：构造组合特征（例如年龄与收入的组合），挖掘潜在关联关系。

超参数调优

树结构控制：

max_depth

设定最大深度限制，防止模型过拟合。

min_samples_split

设置节点分裂所需的最小样本数量。

min_samples_leaf

规定叶子节点包含的最小样本数。

正则化策略：

max_features

限制每次分裂时可选的特征子集大小。

min_impurity_decrease

设定分裂所需达到的最小纯度提升阈值。

模型评估方法

• 交叉验证：采用 k 折交叉验证评估模型的泛化能力。
• 特征重要性分析：借助决策树内置的重要性指标识别关键影响因素。
• 可视化分析：通过决策路径可视化，检查模型逻辑是否符合业务直觉。

六、总结与思考

6.1 核心收获

• 算法本质：ID3 利用信息增益衡量特征区分能力，实现了从数据中自动提取决策规则的过程，体现了“分而治之”的机器学习思想。
• 优化平衡：预剪枝通过牺牲部分训练精度来换取更强的泛化能力，是“偏差-方差权衡”的典型体现。
• 可视化价值：决策树的结构可视化不仅有助于模型解释，还能直观展现特征间的层级依赖与决策流程。
• 演进规律：从 ID3 发展到 C4.5 和 CART，再到集成学习框架，反映出算法由单一模型向集成化、由简单规则向复杂优化演进的趋势。

6.2 实际应用建议

算法选择策略：

• 优先采用 C4.5 或 CART 等改进算法替代原始 ID3，克服其固有缺陷。
• 对于小规模数据或需要强解释性的场景，选择单棵决策树；对于大规模数据或高性能需求场景，推荐使用集成学习方法。

剪枝方案组合：

• 以预剪枝作为基础手段，快速控制模型复杂度。
• 结合后剪枝进一步优化泛化性能，尤其适用于关键业务系统。

特征工程重点：

• 做好特征预处理工作，包括离散化、归一化以及缺失值处理，提高模型稳定性。
• 通过特征选择去除冗余信息，避免维度灾难。

可解释性利用：

• 充分发挥决策树“白盒”特性，生成清晰的决策规则，满足金融、医疗等行业对合规性和透明度的要求。
• 借助可视化工具展示完整决策路径，提升业务人员对模型的信任与接受度。

决策树是机器学习中一种经典且广泛应用的算法，其重要性不仅体现在实际任务中的良好表现，更在于具备清晰直观的决策过程和坚实的数学基础。通过深入理解 ID3 算法的核心原理及其优化路径，能够帮助我们更透彻地把握后续复杂算法的设计逻辑，为应对更高阶的机器学习挑战提供有力支撑。

在真实项目场景中，合理采用决策树以及相应的改进技术，不仅能够维持模型的高度可解释性，还能有效满足性能方面的实际需求。这种兼顾透明度与效率的特性，使其成为连接业务目标与技术落地之间的理想桥梁。

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

分享0 收藏0 回帖

关键词：决策树 randomForest information Informatio rectangle

相关内容：决策树优化剪枝