点云配准算法之-Generalized-ICP（ GICP）

是 否 +2 论坛币

k人 参与回答

经管之家送您一份

应届毕业生专属福利!

求职就业群

赵安豆老师微信：zhaoandou666

经管之家联合CDA

送您一个全额奖学金名额~ !

立即领取

感谢您参与论坛问题回答

经管之家送您两个论坛币！

+2 论坛币

1. 算法概述

Generalized-ICP（简称 GICP）由 Aleksandr Segal 等人在 Robotics: Science and Systems 2009 上提出。该方法将传统的点到点 ICP 和点到面 ICP 统一在一个基于概率与协方差的最小二乘优化框架中。通过为每个点构建局部协方差矩阵，并采用马氏距离衡量配准误差，GICP 能够更鲁棒地估计刚性变换，尤其适用于存在噪声、点云密度不均以及局部平面结构复杂的场景。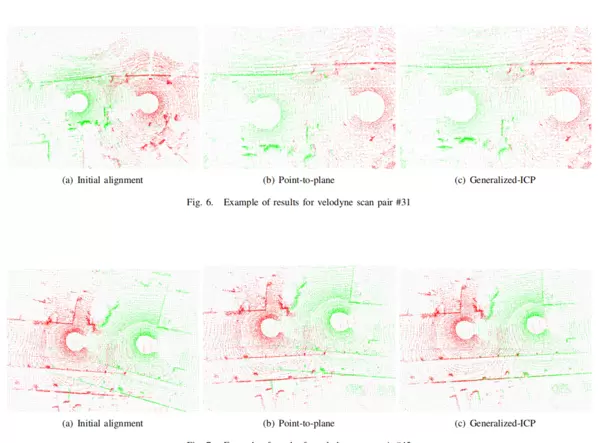

2. 动机与背景分析

传统点到点 ICP 方法依赖欧氏距离最小化对应点之间的偏差，虽然实现简单，但对噪声敏感，且无法有效应对点密度变化或采样方向差异的问题。而点到面 ICP 则通过在目标点法线方向上最小化投影误差，在近似平面区域表现出更快的收敛速度和更高的精度；然而，它仅利用目标点云一侧的几何信息，且高度依赖准确的法向量估计。 GICP 的核心动机在于：源点云和目标点云各自都蕴含了局部几何特征（如局部平面性），这些信息应被同时建模。通过引入概率机制表达这种不确定性，算法能够在配准时融合双向局部结构信息，从而构造出更平滑、更具一致性的误差曲面，提升整体鲁棒性与收敛性能。

3. 主要贡献与创新点

• 统一的概率建模范式：将点云配准问题形式化为极大似然估计（MLE）任务，假设每对匹配点服从以各自局部协方差描述不确定性的联合高斯分布。这一视角自然涵盖了点到点和点到面 ICP 作为特例。
• 局部协方差建模：针对每个点，基于其 k 近邻点集计算协方差矩阵，用于刻画该点周围空间中不同方向上的几何变异程度。例如，在局部平面上，法线方向的方差较小，而切向方向则较大。
• 融合双向不确定性的代价函数：使用形如 $(q_i - R p_i - t)^T (C_{q_i} + R C_{p_i} R^T)^{-1} (q_i - R p_i - t)$ 的马氏距离作为误差项，其中包含了源点与目标点的协方差信息。该代价在局部近似为二次函数，有利于优化过程稳定进行。
• 增强的鲁棒性表现：相较于经典 ICP 方法，GICP 在面对复杂形状、噪声干扰、非均匀采样及部分视角缺失时展现出更强的稳定性，且对初始位姿的依赖程度更低，因此常被后续研究用作基准方法。

4. 关键技术挑战及其应对策略

GICP 致力于解决以下四个核心问题：

1. 如何综合利用源点云与目标点云的局部几何结构？—— 通过分别估计两侧点的局部协方差实现双向信息融合。
2. 如何量化并整合不同方向上的几何不确定性？—— 使用协方差矩阵建模各向异性，并将其嵌入马氏距离度量中。
3. 如何高效求解含协方差项的优化问题？—— 在每次迭代中对非线性代价函数进行线性化处理，转化为标准线性最小二乘问题求解增量变换。
4. 如何在噪声、离群点和密度差异下保持准确性与收敛性？—— 协方差加权机制天然抑制了异常方向的影响，提升了整体稳健性。

其解决方案可概括为：先为每个点估算局部协方差，再将其纳入误差权重设计中，构建基于马氏距离的联合代价函数，最后借助经典的优化工具（如线性化与线性系统求解）迭代更新变换参数。

5. 算法执行流程

以下是 GICP 的主要步骤，以伪代码逻辑呈现，便于理解其实现机制。 输入： 源点云 $ P = \{p_i\} $，目标点云 $ Q = \{q_j\} $，初始变换 $ (R, t) $

1. 局部协方差预估：
   • 对源点云 $ P $ 中每个点 $ p_i $，利用其 k 近邻计算协方差矩阵 $ C_{p_i} $；
   • 对目标点云 $ Q $ 中每个点 $ q_j $，同样计算对应的 $ C_{q_j} $；
   • 通常这两个协方差集合在原始坐标系下独立完成。
2. 外层迭代循环（ICP 框架）：
   1. 应用当前变换 $ (R, t) $ 将源点云映射至目标坐标系： $ p_i' = R p_i + t $
   2. 为每个变换后的点 $ p_i' $ 寻找对应点 $ q_i $（常用最近邻搜索，可设距离阈值过滤无效匹配）。
   3. 对每一对匹配 $ (p_i, q_i) $ 构造合成协方差项： $ S_i = C_{q_i} + R C_{p_i} R^T $
   4. 构建总代价函数： $ E(R,t) = \sum_i (q_i - R p_i - t)^T S_i^{-1} (q_i - R p_i - t) $
   5. 在当前 $ (R,t) $ 处对 $ E(R,t) $ 进行线性化（可通过小角度近似或李代数参数化），得到关于变换增量的线性最小二乘问题。
   6. 求解该线性系统，获得更新量并修正 $ R $ 和 $ t $。
   7. 重复上述过程直至满足收敛条件或达到最大迭代次数。

输出： 最终估计的刚性变换 $ (R, t) $

6. 核心方法详解

6.1 经典ICP算法回顾

标准 ICP 算法的核心思想包含两个基本步骤：

1. 建立两帧点云之间的点对点对应关系；
2. 求解一个最优刚体变换，使得所有对应点之间的距离总和最小。

这两个步骤交替执行，通常经过若干次迭代后可收敛至合理结果。由于现实中难以保证两次扫描完全重叠，因此需设定最大匹配距离阈值，以剔除不可靠的匹配对，避免错误关联影响优化过程。

在点云配准中，d_max?d\_{\max} 是一个关键的阈值参数，主要用于处理第二幅扫描中某些点缺乏对应匹配点的情形。例如，当某个点位于扫描 A 的边界之外时，便无法找到有效对应关系。

大多数 ICP（Iterative Closest Point）算法实现中，d_max?d\_{\max} 的设定体现了收敛性能与配准精度之间的权衡：

• 若该值设置过小，会导致算法视野受限，出现“短视”现象，从而影响整体收敛性；
• 若取值过大，则可能引入错误的点对匹配，使最终变换结果偏离真实最优解。

标准 ICP 算法流程如算法 1 所示。

算法 1：标准 ICP

输入：
两个点云：A = {a_i}, B = {b_i}
初始变换：T_0

输出：
将点云 A 与 B 对齐所需的正确变换 T。

6.2 点到平面 ICP 算法

点到平面（Point-to-Plane）ICP 是一种利用表面法向信息以提升配准效果的 ICP 变体。该方法最早由 Chen 和 Medioni 提出，在处理 2.5D 深度数据时表现出比传统点到点方法更强的鲁棒性和更高的精度。

不同于点到点 ICP 最小化误差项 ∑∣T·b_i m_i∣，点到平面方法最小化的是变换后点沿其对应点表面法线方向的投影误差。换句话说，它优化的是残差向量 (T·b_i m_i) 在由表面法线张成的空间上的分量。

这一目标可通过修改算法 1 中第 11 行的优化步骤实现：

T ← arg min_T ∑_i w_i |η_i · (T·b_i m_i)|

其中 η_i 表示对应点 m_i 处的单位表面法线。

6.3 Generalized-ICP 算法

Generalized-ICP 的核心思想是在标准 ICP 框架的基础上，于算法 1 第 11 步的最小化过程中引入概率建模机制，其余流程保持不变。这种设计在不显著增加计算复杂度的前提下，提升了配准的稳健性，同时保留了 ICP 固有的高效特性。

值得注意的是，点对的对应关系仍基于标准欧氏距离进行搜索，并未采用概率度量方式。这一策略允许继续使用 kd-tree 进行快速最近邻查找，从而维持 ICP 相较于全概率方法的主要优势——速度与简洁性。

由于仅第 11 步涉及概率推导，以下分析聚焦于该步骤的上下文。假设最近点匹配已完成，且两组点云已按对应关系排列为：

A = {a_i}_{i=1,…,N},  B = {b_i}_{i=1,…,N}

即每个 a_i 与 b_i 构成一对候选匹配点。此外，所有满足 ∥m_i T·b_i∥ > d_max 的点对已被预先剔除。

概率模型构建

假设存在一组潜在的真实点集：

= {_i},  B = {b_i}

这些潜在点生成观测到的点云 A 与 B，具体形式为：

a_i N(_i, C_i^A),  b_i N(b_i, C_i^B)

其中 C_i^A 与 C_i^B 分别表示点 a_i 和 b_i 的协方差矩阵，反映其观测不确定性。

进一步假设存在完美对应关系（即几何一致、无遮挡或采样偏差），并设真实刚体变换为 T*，则有如下理想关系：

b_i = T* _i    (1)

对于任意刚体变换 T，定义残差函数：

d_i(T) = b_i T a_i

考虑在真实变换 T* 下的残差分布 d_i(T*)。由于 a_i 与 b_i 分别独立地从高斯分布中采样，可得：

d_i(T*) N(b_i T* _i,  C_i^B + T* C_i^A (T*)^T)

结合等式 (1)，即 b_i = T* _i，均值项为零，因此上式简化为：

d_i(T*) N(0,  C_i^B + T* C_i^A (T*)^T)

最大似然估计

采用最大似然估计（MLE）方法，可对变换矩阵 \( T \) 进行迭代求解：

\[ T = \arg \max_T \prod_i p(d_i(T)) = \arg \max_T \sum_i \log p(d_i(T)) \]

进一步将其转化为最小化问题：

\[ T = \arg \min_T \sum_i d_i(T)^T \left(C_i^B + T C_i^A T^T \right)^{-1} d_i(T) \tag{2} \]

该优化式构成了 Generalized-ICP 的核心步骤。

与标准 ICP 的关系

当设定 \( C_i^B = I \) 且 \( C_i^A = 0 \)，公式 (2) 简化为：

\[ T = \arg \min_T \sum_i \| d_i(T) \|^2 \tag{3} \]

这正是标准 ICP 算法中的误差最小化形式。因此，标准 ICP 可视为 Generalized-ICP 在特定协方差参数下的特例。

与点到平面 ICP 的关系

点到平面 ICP 的优化目标为：

\[ T = \arg \min_T \sum_i \| P_i \cdot d_i \|^2 \tag{4} \]

其中 \( P_i \) 是投影矩阵，将向量投影至对应点 \( b_i \) 的法向所张成的子空间。由于 \( P_i \) 为正交投影矩阵，满足：

\[ P_i = P_i^2 = P_i^T \]

因此有：

\[ \| P_i \cdot d_i \|^2 = d_i^T P_i d_i \]

于是公式 (4) 可重写为：

\[ T = \arg \min_T \sum_i d_i^T P_i d_i \tag{5} \]

对比公式 (5) 与 (2)，可以看出：若令

\[ C_i^B = P_i^{-1}, \quad C_i^A = 0 \tag{6,7} \]

则点到平面 ICP 成为 Generalized-ICP 的一种极限情况。虽然严格意义上 \( P_i \) 不可逆，但可通过一个可逆矩阵 \( Q_i \) 近似，当 \( Q_i \to P_i \) 时，Generalized-ICP 将趋近于点到平面 ICP。

直观理解是：在法线方向上约束较强（即定位精确），而在切平面方向上不确定性高（即位置信息缺失）。

应用：面到面（plane-to-plane）扩展

为了提升配准精度并增强对称性，可进一步扩展 Generalized-ICP 方法，使其同时利用两个点云的局部表面几何信息。最直接的想法是将点云 B 的表面特性引入公式 (7) 中的协方差建模。然而，由于涉及奇异矩阵，直接构造不可行。为此，借鉴点到平面的思想建立合理的概率模型。

基本思想

点云数据实际上是三维曲面的离散采样结果，而非无结构的随机点集。在局部范围内，曲面可近似为平面，因此每个采样点主要在其表面法线方向提供有效约束。

• 法向方向：协方差值极小，表示该方向上的观测置信度高；
• 切平面方向：协方差值较大，表示该方向上的位置信息较弱或不确定。

假设某点的法向为 \( e_1 \)，其对应的协方差矩阵可设为：

\[ \begin{pmatrix} \epsilon & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \]

其中 \( \epsilon \) 为一个极小的正数，表明法向方向具有高度确定性，而切平面上的位置则几乎未知。

协方差矩阵构造

设点 \( b_i \) 的单位法向为 \( \mu_i \)，点 \( a_i \) 的单位法向为 \( \nu_i \)。通过旋转矩阵 \( R_{\mu_i} \) 将标准坐标系对齐至 \( \mu_i \) 方向，则其协方差矩阵定义为：

\[ C_i^B = R_{\mu_i} \begin{pmatrix} \epsilon & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} R_{\mu_i}^T \]

类似地，可构建来自点云 A 的协方差项 \( C_i^A \)，从而实现双向表面约束的融合，提升配准鲁棒性与准确性。

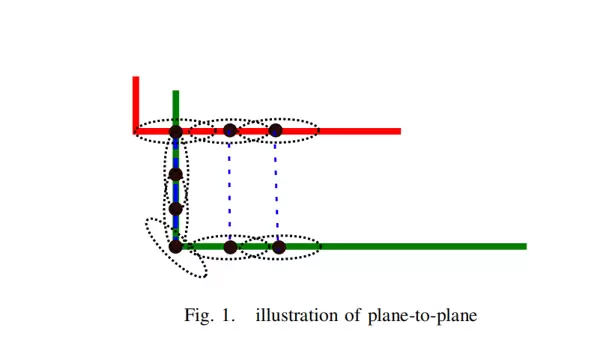
在极端情况下，例如绿色点云的垂直部分错误匹配到红色点云中的同一点时，由于法向量方向不一致，plane-to-plane 方法会自动降低这些误匹配项的权重。此时对应的协方差矩阵趋向于各向同性，导致其在目标函数中的贡献极小。换句话说，这是一种软约束机制：红点沿 x 方向自由移动，绿点沿 y 方向自由移动，因此这类错误匹配对整体配准结果的影响几乎可以忽略。

法向量估计

为了构建表面协方差矩阵，需要为两个点云中的每个点估计其法向量。常用的方法是 PCA（主成分分析）：对每一个点选取其最近的 20 个邻域点，计算局部协方差矩阵并进行特征分解，其中最小特征值所对应的特征向量即为该点的法向量估计。这种方法广泛应用于点到平面 ICP 和 Generalized-ICP 中。

在 Generalized-ICP 框架中，进一步利用该法向构造旋转矩阵，将 ε 分量对齐至表面法线方向。

算法优势与局限

优势

• 更合理的误差模型：结合了两侧点云的局部几何信息，使得代价函数更接近二次型，提升了收敛性能，在包含平面结构和噪声的实际场景中表现稳定。
• 统一的框架设计：可视为点到点与点到面 ICP 的泛化形式；通过调节协方差参数，可在不同模式间灵活切换行为。
• 对密度差异与采样不均更具鲁棒性：协方差能够反映局部区域的采样分布与不确定性，从而缓解因点密度变化带来的影响。

局限性与注意事项

• 计算开销较大：需为每个点计算协方差（涉及 kNN 搜索及 SVD 或特征值分解），并在每次匹配中求解 3×3 矩阵 S 的逆，虽然单次运算小，但总体耗时高于标准点到点 ICP。实际实现中应采用优化策略，如加速近邻搜索、协方差缓存、并行处理以及快速矩阵求逆等。
• 仍对不良匹配敏感：当对应关系出现严重偏差（如大位移或遮挡导致的错误最近邻）时，马氏距离虽能施加惩罚，但无法完全消除其影响；通常还需引入重投票机制、距离阈值或鲁棒损失函数（如 Huber、Tukey）来增强稳定性。
• 退化情形下的问题：在高度结构化的几何环境中（如纯平面或柱面），协方差矩阵可能出现奇异情况，需进行正则化处理；某些场景下仍存在可观测性不足的问题。

实践建议

• 协方差估计参数选择：邻域大小 k（典型范围为 10–30）会影响估计的平滑程度与局部敏感性；对于稀疏或含较多外点的点云应谨慎设置。针对高噪声扫描数据，可在协方差矩阵上添加 (εI) 进行正则化。
• 预处理优化：在计算法线或协方差前，先进行体素网格下采样（voxel grid filtering），可显著提升效率且通常不影响甚至改善配准效果。
• 加权与鲁棒化处理：在线性系统求解过程中，可在代价项中引入鲁棒核函数，以进一步抑制错误对应点对结果的影响。
• 初始变换的重要性：尽管 GICP 相比点到点方法更具鲁棒性，但仍依赖合理的初始位姿估计；在形变较大的情况下容易陷入局部最优，建议使用特征匹配或粗配准提供先验初值。
• 高效实现的关键点：推荐缓存已计算的协方差、并行化协方差与最近邻搜索过程，并对矩阵 S 使用 Cholesky 分解以加速 S^{-1}v 的求解。许多开源库（如 PCL 中的 GICP 实现）已集成上述优化措施。

参考实现与扩展

PCL（Point Cloud Library）提供了 GICP 的官方实现

pcl::GeneralizedIterativeClosestPoint

，并在工程层面进行了多项性能优化，可供直接调用或学习参考。目前大量 SLAM 与 LOAM 类系统在点云配准模块中采用了 PCL-GICP 或其改进版本。

后续研究提出了多种扩展形式，包括 Multi-Channel GICP（融合强度或颜色通道信息）、视觉引导的 GICP，以及面向点云分片或多尺度结构的优化方案。近年来的工作主要聚焦于加速计算、增强鲁棒性以及退化场景的检测与应对。

关键公式汇总

局部协方差矩阵：

C_x = \frac{1}{|N|} \sum_{y\in N(x)} (y - \mu)(y - \mu)^T

配准误差项：

e = q - (R p + t)

融合协方差矩阵：

S = C_q + R C_p R^T

加权代价函数：

e^T S^{-1} e

线性化后的求解系统：

(J^T S^{-1} J)\xi = -J^T S^{-1} e

结论

GICP 通过“局部协方差 + 马氏距离”的概率建模范式，融合了点到点与点到面 ICP 的核心思想，在大多数具有平面结构、噪声干扰或密度不均的真实点云数据中表现出更强的稳健性。它已成为工业界和学术界点云配准任务中的常用基线方法。相较于经典 ICP，GICP 在精度和鲁棒性方面通常更优，但代价是更高的计算复杂度与实现难度。

参考文献

A. V. Segal, D. Haehnel, S. Thrun, “Generalized-ICP”

Robotics: Science and Systems (RSS), 2009.

PCL 相关文档以及源代码，涵盖工业级实现与性能优化方案。

pcl::GeneralizedIterativeClosestPoint

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

分享0 收藏0 回帖

关键词：Generalized Generalize General ICP ALI