Python实现固定效应回归模型实现因果关系推断

是 否 +2 论坛币

k人 参与回答

经管之家送您一份

应届毕业生专属福利!

求职就业群

赵安豆老师微信：zhaoandou666

经管之家联合CDA

送您一个全额奖学金名额~ !

立即领取

感谢您参与论坛问题回答

经管之家送您两个论坛币！

+2 论坛币

众所周知，“相关并不意味着因果关系”是统计学中的一句经典警示。然而，我想指出的是，在满足特定条件的前提下，相关性确实可以反映因果关系。这些条件在计量经济学领域已有广泛研究和讨论。本文将以通俗易懂的方式对这些关键条件进行总结，并解释为何当这些条件不成立时，传统的普通最小二乘法（OLS）无法准确识别因果效应。

随后，我将引入固定效应（FE）模型作为一种有效的解决方案，并通过两组实际数据分析案例，展示如何使用Python实现相关操作。希望通过清晰的研究设计与可靠的分析结果，帮助你更深入地理解因果推断的本质。

相关性何时能代表因果？——前提条件解析

要判断变量x是否对y具有因果影响，必须满足以下三个经典标准：

1. 时间顺序：x的发生必须早于y；
2. 统计关联：x与y之间存在显著的相关性；
3. 排除混杂：x与y之间的关系不能由其他外部因素所解释。

只有同时满足上述三点，我们才有可能从相关性中推断出因果关系。否则，所谓的“关系”可能只是表象，甚至是误导性的。

仅凭相关性推断因果往往不可靠

图（A）形象地说明了为什么直接从相关性得出因果结论是危险的。

以冰淇淋销量与鲨鱼袭击事件为例：数据显示两者在夏季呈现高度正相关。但这是否意味着吃冰淇淋会增加遭遇鲨鱼的风险？显然不是。这种看似强烈的关联实际上是由第三个变量驱动的——天气炎热的夏季。

具体来看：

• 首先，鲨鱼袭击并不会因为某人购买了冰淇淋而发生；
• 其次，该相关性仅在特定季节出现，并不具备普遍性；
• 最关键的是，二者的关系完全可以被“夏季高温”这一共同诱因而解释。

混杂因素的存在导致虚假关联

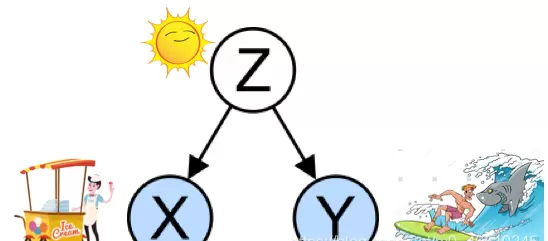
如图（B）所示，冰淇淋销售量（x）和鲨鱼袭击次数（y）都受到夏季气温（z）的影响。这里的气温就是一个典型的混杂因素（Confounding Factor）。它同时作用于自变量x和因变量y，从而制造出一种看似相关实则无因的假象。

在实证研究中，若未能识别并控制这类混杂变量，就可能导致错误的因果推论。尤其当这些因素难以观测或未被记录时，问题更加严重。解决之道在于尽可能将潜在的混杂因素纳入模型，使其变为可观测、可控制的变量。

内生性问题：相关系数可能毫无意义

当存在一个未被控制的混杂因素能够解释x与y之间的关系时，我们就说x具有内生性。此时，即使OLS估计得到了一个显著的回归系数，这个系数也可能完全失真——它可能偏高、偏低，甚至符号相反。

例如，你能说“冰淇淋销售促进了鲨鱼袭击”吗？尽管数据上显示正相关，但由于内生性问题，这一结论毫无依据。因此，在存在内生性的背景下，不应依据相关方向或大小做出任何实质性判断。

如何科学衡量X对Y的真实影响？

要评估某个处理（treatment）的真实效果，我们必须比较个体在接受处理与未接受处理两种状态下的结果差异。换句话说，我们需要知道“如果这个人没有接受干预，会发生什么”——这被称为反事实（counterfactual）推理。

随机对照试验（RCT）：因果推断的黄金标准

在理想情况下，随机对照试验（RCT）被认为是确定因果关系的最佳方法（Shadish et al., 2002）。通过将个体随机分配至处理组和对照组，可以确保两组在可观测与不可观测特征上的分布基本一致。这样一来，最终观测到的结果差异就可以归因于处理本身。

从统计角度看，普通最小二乘法（OLS）依赖的核心假设正是：自变量x与误差项u之间无相关性，即 E(Xu) = 0。这一假设排除了内生性问题。而在随机化条件下，由于分配过程独立于所有潜在影响因素，该假设自然成立。

OLS模型通常表示如下（i 表示第 i 个个体，共有 N 个个体），其矩阵形式也已在图中给出。

然而，在现实中，开展RCT往往面临诸多限制：

• 成本高昂、耗时长；
• 公众参与意愿低，沟通难度大；
• 某些情境下涉及伦理问题，例如不允许人为延迟患者治疗以设立对照组。

因此，许多实际问题无法通过RCT来解决。那么，还有哪些可行路径？近年来，越来越多的研究者转向准实验设计（quasi-experimental design），并取得了令人信服的成果。“准”并非“假”，而是指在缺乏随机化的前提下，尽可能模拟RCT的逻辑结构。

准实验设计：逼近“同样有效”的替代方案

尽管无法实施随机分配，但准实验设计力求使处理组与对照组之间唯一的系统性差异就是“是否接受处理”。常见的方法包括：

• 回归不连续设计（Regression Discontinuity, RD）
• 双重差分法（Difference-in-Differences, DiD）
• 固定效应模型（Fixed-Effects Model, FE）

回归不连续设计（RD）：利用阈值划分群体

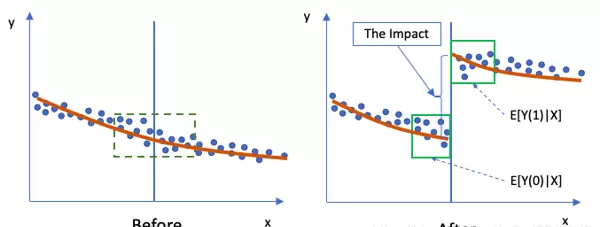
RD设计的核心思想是比较那些刚好高于与刚好低于某一决策阈值的个体。如图（D）中的“Before”阶段所示，绿色框内的个体在各项特征上极为相似。

进入“After”阶段后，其中一组因跨越阈值而接受干预，另一组则未受影响。若在此处观察到结果变量出现明显的跳跃或不连续变化，则可将其归因于干预措施的效果。

这种方法巧妙地规避了选择偏差问题，因为在临界点附近，个体是否被处理近乎“随机”，从而为因果识别提供了有力支持。

在评估某一干预措施的影响时，我们通常关注“After”阶段（标记为“1”）对结果变量Y的期望值，即E[Y(1)|X]，而“Before”阶段（标记为“0”）对应的则是E[Y(0)|X]。如小绿色框所示，在该区域内所有个体的协变量X非常接近，因此可认为“前”与“后”两个时期的X保持一致。此时，所得出的回归不连续性（RD）估计结果将趋近于随机对照试验（RCT）的效果。

面板数据（Panel Data）

面板数据，也被称为纵向数据或跨时间序列数据，指的是在多个时间点上对同一组个体进行观测所获得的数据集。这类数据结合了横截面和时间序列的特点，能够提供更丰富的信息结构。一个基本的面板数据回归模型形式类似于公式（1），其中???? 和 ???? 表示待估参数，i 和 t 分别代表个体和时间维度。

使用面板数据的优势在于它允许研究者控制不可观测的异质性，并能更准确地识别变量之间的关系。例如，在Python中广泛使用的Pandas库，其名称正是来源于“Panel Data”的谐音，这一命名既巧妙又富有亲和力。

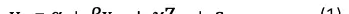
假设可在OLS中完全控制所有影响因素

设想我们可以构建一个完全详尽的线性模型来分析婚姻状况是否会影响个人收入。假设模型中包含了所有可能影响收入的因素：

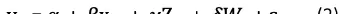
其中 y_it 表示个体i在时间t的收入水平，x_it 为其婚姻状态，Z_it 是随时间变化的可观测变量（如年龄、工作年限等），W_i 是不随时间改变的特征（如种族、出生地等），而 ????_it 为误差项。若确实能够穷尽所有相关变量，则通过普通最小二乘法（OLS）得到的系数???? 将是无偏估计。

当在面板数据上应用OLS时，这种方法常被称为“池化OLS”（Pooled OLS）。理论上，只有当各观测之间相互独立时该方法才成立。然而在实际中，由于同一个体在不同时间点的数据往往存在自相关，这一前提很难满足。尽管如此，如果个体内部的相关性较弱且影响有限，采用池化OLS仍可能是可接受的近似处理方式。

现实中难以在OLS中涵盖全部变量

遗憾的是，现实中我们几乎不可能列出所有影响因变量的潜在因素。假设我们将上述模型中的 Z_it 和 W_i 忽略，仅将 y_it 对 x_it 进行回归。已知婚姻状况（x_it）、年龄（Z_it）以及种族（W_i）之间很可能存在相关性。一旦未将这些变量纳入模型，它们就会被吸收进误差项 ????_it 中，导致 x_it 与误差项相关，从而使OLS估计产生内生性问题。

这种情况下，婚姻状况成为内生变量，使得所估计的???? 系数无论正负都失去了因果解释的意义。因此，遗漏重要变量会严重损害模型的有效性，任何基于此类设定得出的结论都将不可靠。

固定效应模型（Fixed Effects Model）

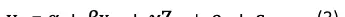
为了缓解遗漏变量带来的偏差，可以引入固定效应模型。其中 ????_i 被称为个体固定效应，用于捕捉那些不随时间变化但可能影响结果的个体特征，如性别、种族乃至某些稳定的个性特质。y_it 和 x_it 分别表示个体i在时间t的收入与婚姻状况，Z_it 则涵盖其他随时间变动的控制变量。

该模型假设误差项 ????_it 与所有解释变量无关；若此假设不成立，则仍可能存在因遗漏变量而导致的估计偏误。

如何估计方程（3）？大多数教材中呈现的基本形式如方程（3）所示。当只涉及两个个体（i=0,1）时，可以直接写出表达式。而在包含N个个体（i=1,…,N）的情形下，????_i 可以理解为一组共(N1)个虚拟变量 D_i 的简写，每个对应一个个体并拥有独立系数，如方程（4）所示——这也是回归输出中最常见的形式。

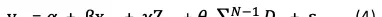
双重差分法是固定效应模型的特例

事实上，双重差分法（Difference-in-Differences, DiD）可以被视为固定效应框架下的一个特殊情形。

图（E）：DiD 方法示意图

DiD的核心思想十分直观：首先计算“Before”阶段处理组与对照组之间结果变量的平均差异，记作“A”；然后在“After”阶段重复同样的计算，得到“B”；最后取两者之差，即“A”与“B”的差值，称为“第二重差分”，标记为“C”。“C”反映了两组结果变化趋势的差异，而这部分差异可归因于政策或干预的因果效应。

从面板数据的角度看，DiD可通过“差分消除”（differencing out）那些不随时间变化的混杂因素，从而从固定效应模型中推导而出。由于这些潜在混淆变量已被剔除，最终估计的影响具有更强的因果含义。典型的建模设定如公式（5）所示：

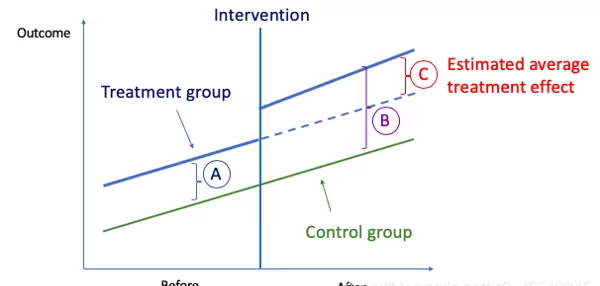
设个体i属于处理组（x_i = 1）或对照组（x_i = 0），并且处于干预前（t_i = 0）或干预后（t_i = 1）阶段。那么干预后的净效应由 ????_2 表示，如图（E）中的“C”所示。该系数可通过以下方式识别：

需要注意的是，DiD与一般固定效应模型的关键区别在于：引起变化的干预必须是外生的，即不由个体自主选择决定。例如，某州政府统一调整最低饮酒年龄法规，这种政策变动就是典型的外生冲击，适合作为DiD分析的基础。

固定效应数据分析实例1 — 投资与市场价值的关系

公司投资行为背后的驱动因素一直是经济学研究的重要课题，大量学术文献探讨了影响企业投资决策的各种变量。Grunfeld提出，企业的市场价值是解释和预测其投资水平的关键指标。本文将借助Grunfeld数据集（可通过statsmodels.datasets获取）来展示如何应用固定效应模型进行实证分析。该数据集在计量经济学领域具有重要地位，类似于机器学习中常用的鸢尾花数据集，被广泛用于教学与研究。事实上，一篇题为“Grunfeld数据集50年”的论文也强调了其长期的学术影响力。

该面板数据涵盖了11家美国公司在20年间的年度观测值，涉及的企业包括：IBM、通用电气、美国钢铁、大西洋炼油、钻石比赛、西屋电气、通用汽车、固特异、克莱斯勒、联合石油等。在处理此类数据时，通常将“firm”（企业）和“year”（年份）设为多层索引结构，以便于建模分析。固定效应模型可表示如下，其中 表示个体层面的企业效应（entity effects），而 " alt="图片13"> 则代表时间效应（time effects）。

另一种表达方式是引入虚拟变量：D_j 代表第 j 家公司的企业虚拟变量，I_t 则为第 t 年的时间虚拟变量，如公式所示：" alt="图片14">

from statsmodels.datasets import grunfeld
data = grunfeld.load_pandas().data
data = data.set_index(["firm","year"])
print(data.head())

" alt="图片15">

为了估计固定效应模型，可以使用 linearmodels.panel 模块中的 PanelOLS 方法。 该方法能够控制不可观测的企业特定效应，即通过为每个企业设置虚拟变量的方式捕捉那些不随时间变化但跨企业不同的因素。由于存在11家企业，模型会自动生成N-1=10个虚拟变量以避免多重共线性。 下面展示了两种等价的代码实现方式，二者回归结果一致。

# 方法一：显式添加常数项并指定变量
from linearmodels.panel import PanelOLS
import statsmodels.api as sm
exog = sm.add_constant(gf[['value','capital']])
grunfeld_fe = PanelOLS(gf['invest'], exog, entity_effects=True, time_effects=False)
grunfeld_fe = grunfeld_fe.fit()
print(grunfeld_fe)

# 方法二：使用公式接口
grunfeld_fe = PanelOLS.from_formula("invest ~ value + capital + EntityEffects", data=gf)
print(grunfeld_fe.fit())

" alt="图片16">

回归结果显示，“value”（市场价值）的系数为0.1101，在95%置信水平下具有统计显著性。这支持了Grunfeld的核心结论：企业的高市场价值与其高水平的投资之间存在正向因果关系，即市场估值越高的公司倾向于进行更多的资本支出。

进一步地，我们也可以同时纳入企业固定效应和时间固定效应，以控制可能随时间共同变动的外部冲击（如宏观经济波动）。以下代码实现了这一扩展模型：

# 同时包含企业和时间效应 — 方法一
from linearmodels.panel import PanelOLS
import statsmodels.api as sm
exog = sm.add_constant(gf[['value','capital']])
grunfeld_fet = PanelOLS(gf['invest'], exog, entity_effects=True, time_effects=True)
grunfeld_fet = grunfeld_fe.fit()  # 注：此处应为 grunfeld_fet 而非 grunfeld_fe，原文可能存在笔误
print(grunfeld_fet)

# 方法二：公式法
grunfeld_fet = PanelOLS.from_formula("invest ~ value + capital + EntityEffects + TimeEffects", data=gf)
print(grunfeld_fet.fit())

" alt="图片17">

即便在加入时间效应后，主要结论依然稳健，“value”的正向影响未发生根本改变。

固定效应模型应用实例二：啤酒税与交通事故死亡率

提高啤酒税是否有助于降低交通致死率？这是一个具有重大公共政策意义的问题。观察发现，一些州降低了酒精饮料税收，随之而来的是更高的交通事故死亡率。但这是否意味着降低啤酒税直接导致了更多死亡？要识别这种因果关系，需谨慎控制潜在混杂因素。本部分采用Stock与Watson在其经典教材《计量经济学导论》中使用的“fatalities”数据集来进行分析。

import pandas as pd
import numpy as np
import seaborn as sns
fatalities = pd.read_csv('/fatality.csv')
fatalities.head()

" alt="图片18">

数据集中主要变量说明如下：

• mrall：每百万车辆行驶里程中的总死亡人数
• beertax：每加仑啤酒的税收金额
• mlda：法定最低饮酒年龄
• jaild：对酒驾者实施强制监禁的政策标识
• comserd：是否要求酒驾者参与社区服务
• vmiles：每位驾驶员的平均年行驶里程
• unrate：州级失业率

通过构建面板数据模型并引入州固定效应或时间固定效应，可以更准确地评估啤酒税对交通安全的影响，从而为政策制定提供依据。

perinc 表示人均个人收入。为了观察年度趋势，我计算了每年的平均值，用以展示每年的平均啤酒税以及相应的死亡率情况。数据显示，1982年至1984年期间的平均啤酒税水平高于1986年至1988年期间。

avg = fatalities.groupby('year')['mrall','beertax'].mean()
avg

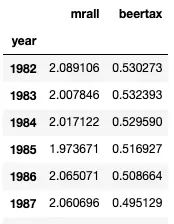
接下来，我使用 `seaborn` 库来可视化啤酒税与总体死亡率之间的相关性关系。通过设置绘图风格为“darkgrid”，并采用联合回归图（jointplot）的形式进行展示，能够更清晰地呈现两者间的线性趋势。

sns.set(style="darkgrid")
g = sns.jointplot("beertax", "mrall", data=avg, kind="reg", color="m", height=6)

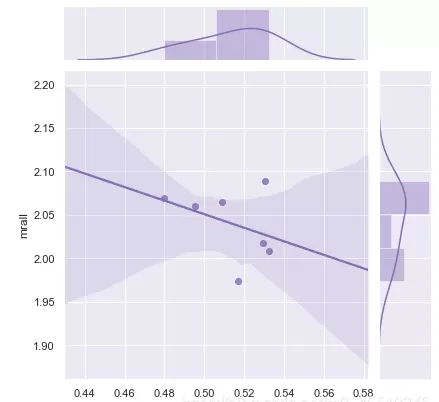
那么，是否可以从中推断出因果关系？为了验证这一点，我采用了固定效应模型进行分析，并对比了三种不同的建模方式：一是包含实体和时间双重效应的模型；二是仅考虑实体效应的模型；三是汇总普通最小二乘法（Pooled OLS）模型。

模型 1: 实体效应 + 时间效应
模型 2: 实体效应（Entity_effects）
模型 3: 汇总OLS

其中，D_j 表示州 i 的虚拟变量，I_t 则代表时间 t 的虚拟变量，用于控制不随个体变化但随时间变动的因素。

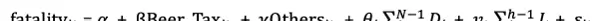
该模型设计可有效控制两类潜在遗漏变量的影响：其一，是各州内部不随时间改变的特征，例如当地文化或居民对饮酒行为的态度；其二，是对所有州具有普遍影响但随时间波动的宏观因素，如联邦政策调整或经济周期变化等。

如何判断应选择哪种模型设定更为合适？这可以通过“可合并性检验”（Poolability Test）来进行判断。许多统计模块已内置此检验结果。下图展示了相关输出内容——这是针对“无需使用固定效应”的原假设所进行的F检验。在模型1中，F统计量为40.158，对应的p值为0.0，表明我们可以强烈拒绝原假设，从而支持采用固定效应模型的合理性。

模型1：实体效应 + 时间效应

# 方法一 编码实现
from linearmodels.panel import PanelOLS
import statsmodels.api as sm
exog = sm.add_constant(fatalities[['beertax','mlda','jaild', 'comserd','vmiles','unrate','perinc']])
fe = PanelOLS(fatalities['mrall'], exog, entity_effects=True, time_effects=True)
fe = fe.fit()
print(fe)

# 方法二 公式法实现
from linearmodels.panel import PanelOLS
fe = PanelOLS.from_formula("mrall ~ beertax + mlda + jaild + comserd + vmiles + unrate + perinc + EntityEffects + TimeEffects", data=fatalities)
print(fe.fit())

根据模型1的结果，啤酒税与交通事故死亡率之间存在显著的负向关联，其系数为 -0.4649。这意味着，提高啤酒税与降低死亡率之间具备统计上的因果联系，即更高的啤酒税可能有助于减少交通致死事故的发生。

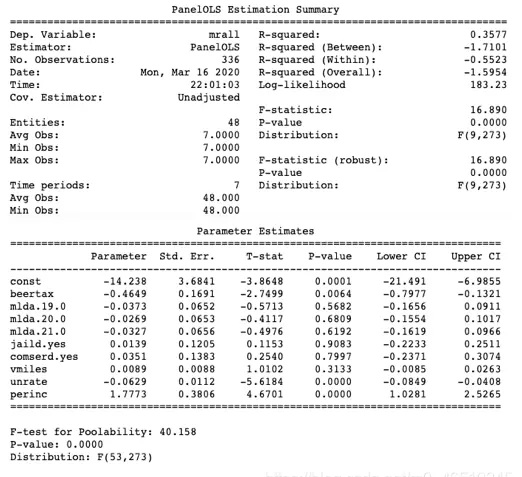
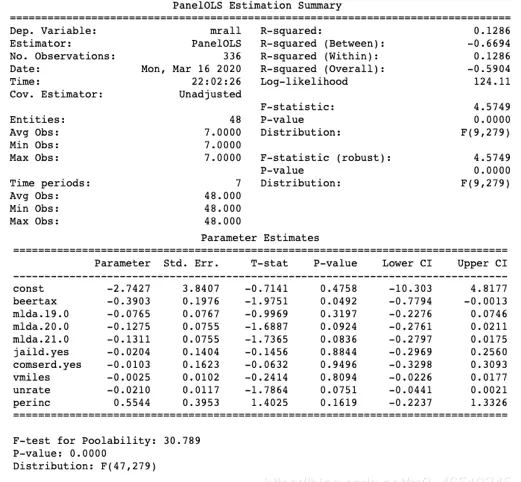
模型2：实体效应

关于三个模型中R-squared值的解释如下：模型1的R为0.3577，明显高于模型2的0.1286，说明前者对数据的拟合程度更优。而模型3的R达到0.4662，虽然数值更高，但由于其基于合并OLS方法构建，属于错误设定的模型（如前述公式(1)和(2)所示），未能处理内生性问题，因此不能用于因果推断。

# 方法一 实现代码
from linearmodels.panel import PanelOLS
import statsmodels.api as sm
exog = sm.add_constant(fatalities[['beertax','mlda','jaild','comserd','vmiles','unrate','perinc']])
fe2 = PanelOLS(fatalities['mrall'], exog, entity_effects=True, time_effects=False)
fe2 = fe2.fit()
print(fe2)

# 方法二 公式法实现
from linearmodels.panel import PanelOLS
fe2 = PanelOLS.from_formula("mrall ~ beertax + mlda + jaild + comserd + vmiles + unrate + perinc + EntityEffects", data=fatalities)

F-test for poolability

模型3：汇总OLS回归分析

方法一：使用 linearmodels 库中的 PanelOLS 进行建模。首先导入必要的模块，包括 statsmodels.api 用于添加常数项，以及 PanelOLS 用于构建面板数据的普通最小二乘模型。

选取自变量 beertax、mlda、jaild、comserd、vmiles、unrate 和 perinc，并通过 sm.add_constant() 添加截距项。因变量为 mrall，基于 fatalities 数据集进行建模。设置 entity_effects 和 time_effects 均为 False，表示不引入个体或时间固定效应。

代码实现如下：

from linearmodels.panel import PanelOLS
import statsmodels.api as sm
exog = sm.add_constant(fatalities[['beertax','mlda',
'jaild','comserd','vmiles','unrate','perinc']])
pooledOLS = PanelOLS(fatalities['mrall'], exog,
entity_effects=False, time_effects=False)
pooledOLS = pooledOLS.fit()
print(pooledOLS)

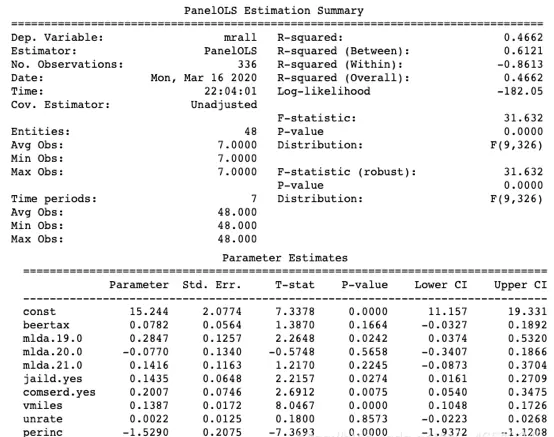
方法二：采用公式方式构建相同的汇总OLS模型。该方法更简洁，直接通过 from_formula 函数定义回归方程。

公式表达式为 "mrall ~ beertax + mlda + jaild + comserd + vmiles + unrate + perinc"，同样基于 fatalities 数据集拟合模型，并输出结果。

# Coding method 2
from linearmodels.panel import PanelOLS
pooledOLS = PanelOLS.from_formula("mrall ~ beertax  +
mlda + jaild + comserd + vmiles + unrate  + perinc ",
data=fatalities)
print(pooledOLS.fit())

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

分享0 收藏0 回帖

关键词：python 因果关系 回归模型 固定效应 fixed-effect