13.3
对中国GDP时间序列数据的处理,重点在于平稳性检验、自相关分析以及模型预测。以下是具体操作流程与分析逻辑。
核心分析步骤:
- 平稳性判断:若自相关函数(ACF)呈现缓慢衰减趋势,则表明原序列可能不具备平稳性。
- 模型类型识别:
- AR(p) 模型:偏自相关函数(PACF)在第 p 阶后截尾,而 ACF 缓慢衰减。
- MA(q) 模型:ACF 在第 q 阶后截尾,PACF 缓慢衰减。
- ARMA(p,q) 模型:两者均表现为缓慢衰减。
- 残差白噪声检验:建模完成后需对残差进行 ACF/PACF 分析,并结合 Q 检验判断其是否为白噪声。若 Q 检验不显著,则说明模型拟合充分。
以下为执行的相关 do 命令:

冷知识补充:命令中 gen year = _n + 1977 的作用是生成年份变量,假设观测从1978年开始,其中 _n 表示当前观测序号。
13行命令输出结果分析
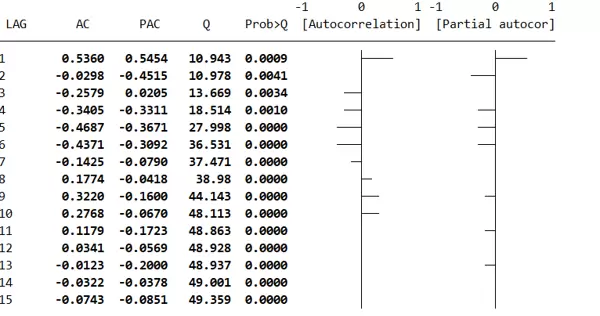
根据表格内容可得:
- ACF 特征:
- 滞后1阶的自相关系数较强,达到0.5360;
- 滞后2阶迅速下降至接近0(-0.0298);
- 滞后3至6阶出现负相关,尤其滞后5阶达-0.4687;
- 滞后8至10阶转为正相关;
- 整体呈现“震荡衰减”模式,暗示可能存在周期性或季节性结构。
- PACF 特征:
- 滞后1阶较高(0.5454),滞后2阶为负值(-0.4515),之后逐步减小;
- 即使到滞后5阶仍为-0.3671,显示高阶滞后项仍有直接影响;
- 未见明显截尾现象,提示可能适用 ARMA 或 ARIMA 类模型。
- Q 检验结果:
- 所有滞后阶数对应的 p 值均小于0.01,表明序列显著非白噪声,存在明显的自相关结构。
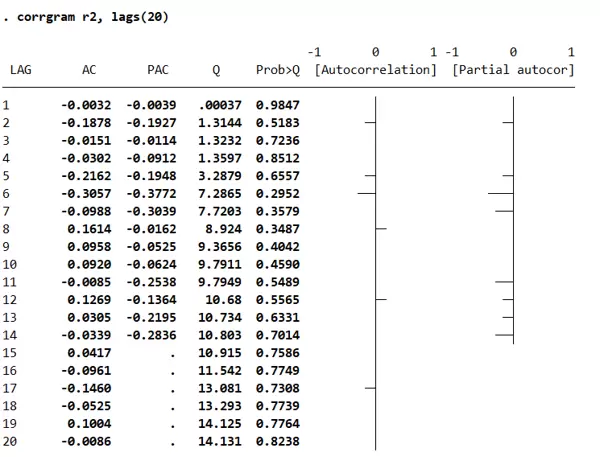
19行命令输出结果解读
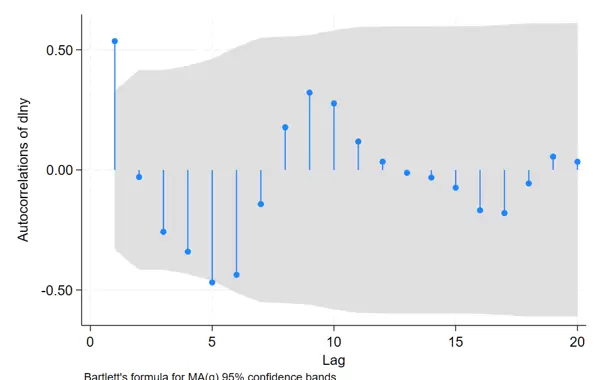
图中阴影部分代表置信区间。若某阶自相关系数落在该区域之外,则认为其显著异于零。
- 仅滞后1阶和滞后5阶的 ACF 落在置信区间外,其余各阶均不显著。
- 这种“稀疏且振荡”的显著模式,既非典型截尾也非典型拖尾。
该模式可能暗示以下几种情况:
- 可能是一个高阶 AR 模型(如本题所示),其中只有特定滞后项具有解释力;
- 或者存在季节性 ARIMA 结构,前提是数据本身具备季节特征;
- 也可尝试使用简单的 ARMA(1,1) 模型并检查残差,必要时引入季节性成分(例如 SARIMA(1,0,1)×(1,0,1),若认为5阶反映季节周期)。
一阶自回归模型(AR(1))拟合与预测
采用 AR(1) 进行建模与预测后的误差分析如下:
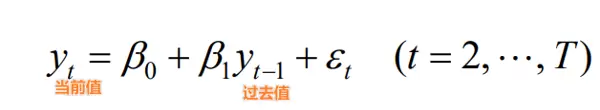


最终预测偏差为 -895.95832,表示模型高估了约895.90347亿元的实际值。
高阶自回归模型(AR(p))分析
为进一步提升模型精度,考虑更高阶的 AR 模型:
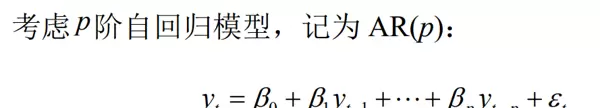

AR 阶数选择的方法冲突与解决
方法一:基于信息准则(AIC 与 BIC)
- 原理:权衡模型拟合优度与参数复杂度,数值越小越好。
- 计算过程:
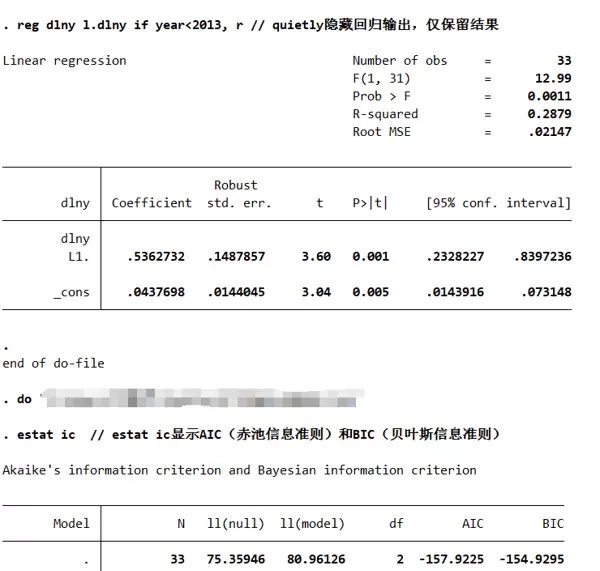
- AR(1):AIC = -157.9223,BIC = -154.9293;
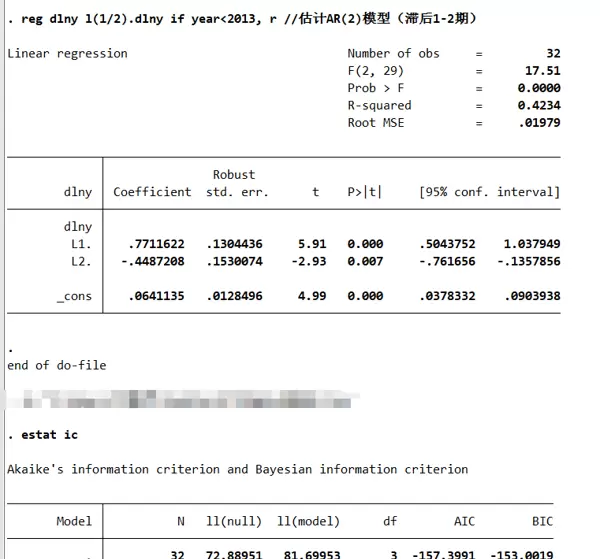
- AR(2):AIC = -157.3987,BIC = -153.0015。
- 结论:由于 AR(1) 的 AIC 和 BIC 更小,信息准则支持选择 AR(1)。
方法二:序贯 t 规则(Sequential t-rule)
- 原理:从高阶开始逐步降阶,剔除不显著的最高阶滞后项,直至保留最后一个显著项为止。
- 实施步骤:
- 在 AR(3) 中,三阶滞后项 `L3.dlny` 的 p 值为 0.906,极不显著,故拒绝 AR(3);
- 在 AR(2) 中,二阶滞后项 `L2.dlny` 的 p 值为 0.007,在 1% 水平上显著。
- 结论:依据此规则应选择 AR(2)。
两种方法结论不一致:
- 信息准则 → 推荐 AR(1)
- 序贯 t 规则 → 支持 AR(2)
最终决定选用 AR(2),原因如下:
- 避免遗漏变量偏差:若真实过程为 AR(2),但错误采用 AR(1),将忽略显著的 `L2.dlny` 项,导致估计有偏。
- 残差诊断结果更优:对比两个模型的残差 Q 检验发现:
- AR(1) 残差存在自相关,说明模型未能完全提取信息;
- AR(2) 残差无自相关,表明模型已充分捕捉序列动态特征。
因此,综合理论合理性与诊断效果,优先选择 AR(2) 模型。
AR(2) 模型下的最终预测偏差为 -680.85149,即高估了680.85149亿元。
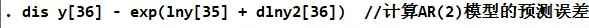
进一步验证显示,AR(2) 的残差通过了白噪声检验,无显著自相关。
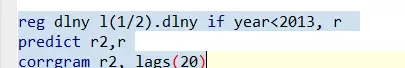




 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







