训练营介绍
2025年昇腾CANN训练营第二季正式开启,依托CANN开源开放的全场景能力,推出面向不同开发阶段人群的系列课程,涵盖零基础入门、码力强化特辑以及真实开发者案例解析等内容。无论你是初学者还是进阶开发者,都能通过系统学习快速掌握算子开发核心技能。
完成指定课程并通过考核,即可获得Ascend C算子中级认证证书,并有机会参与社区任务赢取华为手机、平板设备及开发板等丰富奖品。
报名入口:
https://www.hiascend.com/developer/activities/cann20252#cann-camp-2502-intro

引言:从硬件指令到数学创新
在实际的算子开发过程中,我们通常会直接调用如
Exp(x)和
Tanh(x)这类由硬件微码支持的intrinsic指令,这些指令执行效率极高。
然而,学术研究不断推陈出新。设想某天一篇顶会论文提出一个全新激活函数:
$$f(x) = x \cdot \ln(1 + e^{x^2})$$查阅Ascend C API文档后却发现并无现成实现。此时开发者面临两种选择:
方案一:组合法
通过调用多个基础操作进行拼接,例如使用
MulLnExpAdd等指令逐步构建目标函数。
缺点:涉及多次内存读写(IO),性能受限;同时多步非线性运算易导致累积精度损失。
方案二:拟合法
采用多项式逼近方式,用形如 $P(x) = a_0 + a_1 x + a_2 x^2 + \dots$ 的表达式来近似原函数。
优势:仅包含乘加运算(FMA),可在Vector单元上高效流水线运行,显著提升执行速度。
本文将带你掌握如何化身“数学魔术师”,利用基本算术操作构造复杂函数逻辑。
一、图形化理解:用直线逼近曲线
函数拟合的核心思想是在特定区间内,使用一条“可弯曲的线”——即多项式——尽可能贴近原始目标曲线。多项式的阶数越高,其形状越灵活,拟合效果也越精确。
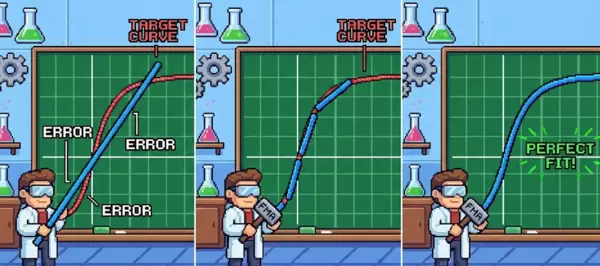
二、关键技术:霍纳法则(Horner's Rule)
假设我们已通过泰勒展开或Remez算法获得了一个三阶近似多项式:
$$P(x) = c_0 + c_1 x + c_2 x^2 + c_3 x^3$$若按常规方法计算,则需分别求出
x2 = x*xx3 = x2*xres = c0 + c1*x + c2*x2 + c3*x3共需3次乘法与3次加法,且存在复杂的依赖关系,不利于并行优化。
霍纳法则提供了一种更优结构,将上述表达式重写为嵌套形式:
$$P(x) = c_0 + x \cdot (c_1 + x \cdot (c_2 + x \cdot c_3))$$该结构天然适配Ascend C中的
FMA (Fused Multiply-Add)指令,其语义为
Mad(d, a, b, c)表示 $d = a \times b + c$。
具体计算流程如下:
reg = c3Mad(reg, x, reg, c2)Mad(reg, x, reg, c1)Mad(reg, x, reg, c0)整个过程仅需3条FMA指令,且具备良好的流水线特性,极大提升了执行效率。
三、实战演练:实现FastGELU算子
GELU函数的标准形式包含复杂的
erf运算,开销较大。工程中常用以下近似公式替代:
$$\text{GELU}(x) \approx 0.5x (1 + \tanh(\sqrt{2/\pi}(x + 0.044715 x^3)))$$其中最耗时的部分是
Tanh的计算。若限定输入范围在 $[-3, 3]$ 内,可考虑对 $\tanh(x)$ 使用四阶多项式拟合,或直接对整体函数进行逼近。
为便于演示,我们实现一个简化版本:$y = \sum_{i=0}^{4} c_i x^i$。
3.1 系数准备(Coefficients)
在Host端或Kernel初始化阶段预加载所需系数值。
// 假设这是通过 scipy.optimize.curve_fit 算出来的最优系数
const float COEFF[] = {0.0f, 0.5f, 0.1f, -0.01f, 0.001f}; // 仅做示例3.2 核函数实现(Compute)
编写核心计算逻辑,利用霍纳法则高效执行多项式求值。
__aicore__ inline void Compute(int32_t i) {
LocalTensor<float> xLoc = inQueueX.DeQue<float>();
LocalTensor<float> yLoc = outQueueY.AllocTensor<float>();
// 1. 广播系数到向量
// 我们需要把标量 c0, c1... 变成全 1 的向量,或者利用标量广播指令
// Ascend C 的 Muls/Adds 支持标量,但 Mad 指令通常需要向量
// 最佳实践:在 Init 阶段把系数 Duplicate 到 UB 的保留区域
// 2. 霍纳法则计算 (Horner's Method)
// P(x) = c0 + x(c1 + x(c2 + x(c3 + x*c4)))
// Step 1: Init with highest order coeff
// yLoc = c4
Duplicate(yLoc, COEFF[4], tileLength);
// Step 2: yLoc = yLoc * x + c3
// Mad(dest, src1, src2, src3) -> dest = src1 * src2 + src3
// 注意:具体 Mad 指令参数顺序需查阅 API 手册,通常是 dest = src1 * src2 + src3
Mad(yLoc, yLoc, xLoc, COEFF[3], tileLength); // 伪代码:支持标量 c3 广播
// Step 3: yLoc = yLoc * x + c2
Mad(yLoc, yLoc, xLoc, COEFF[2], tileLength);
// Step 4: yLoc = yLoc * x + c1
Mad(yLoc, yLoc, xLoc, COEFF[1], tileLength);
// Step 5: yLoc = yLoc * x + c0
Mad(yLoc, yLoc, xLoc, COEFF[0], tileLength);
// 计算完成,yLoc 中即为拟合结果
outQueueY.EnQue(yLoc);
inQueueX.FreeTensor(xLoc);
}3.3 精度优化策略:分段拟合
多项式拟合存在明显局限:当定义域过宽时,低阶多项式难以维持高精度。例如,在 $[-100, 100]$ 范围内拟合高度非线性的GELU函数,四阶多项式显然不够。
解决方案:分段拟合(Piecewise Fitting)
结合上期所学的
Select指令,根据不同输入区间选择最优计算路径:
- 区间 A ($|x| < 3$):函数变化剧烈,采用五阶多项式实现高精度拟合。
- 区间 B ($x \ge 3$):趋于线性区域,可用 $y=x$ 或简单线性表达式代替。
- 区间 C ($x \le -3$):进入饱和区,输出恒定为 $y=0$。
// 伪代码:分段处理
Abs(absX, xLoc);
Compare(maskA, absX, 3.0f, CMP_LT); // MaskA: |x| < 3
// 计算多项式结果
ComputePoly(polyRes, xLoc);
// 组合结果
// 如果在区间 A,取 polyRes;否则检查是否 > 3...
// 这里简化为:GELU 在 x>3 时约等于 x,在 x<-3 时约等于 0
// y = (x > 3) ? x : 0 -> Relu(x)
// 最终混合: Select(res, maskA, polyRes, Relu(x))四、性能对比分析:拟合 vs 组合法
| 方法 | 指令数量 | 延迟 (Latency) | 精度 |
|---|---|---|---|
| 组合法 (Exp+Div+Add) | 5~8 条高延迟指令 | 高(Exp耗时为Add的10倍以上) | 高(符合IEEE 754标准) |
| 拟合法 (Mad * 4) | 4 条低延迟指令 | 极低(可实现流水线满载) | 中(取决于多项式阶数) |
在多数对绝对精度要求不苛刻的
1e-7推理场景下,多项式拟合方案通常能带来
3~5倍的性能提升。
五、总结与展望
数学函数拟合是Ascend C高性能算子开发的关键技术之一,属于进阶优化的必修内容。掌握霍纳法则、分段处理与多项式逼近方法,不仅能有效降低计算延迟,还能在保证足够精度的前提下大幅提升执行效率。未来面对新型函数需求时,你将不再受限于现有API,而是能够主动设计高效的定制化实现方案。
实现:通过霍纳法则与 Mad 指令,构建高效的流水线运算结构,提升计算吞吐效率。

工具:借助 Host 端的 Python 或 Matlab 工具,预先完成拟合系数的计算与优化。
技巧:采用分段拟合策略,有效应对大区间内函数逼近的精度下降问题,确保整体误差可控。
掌握该方法后,你将能够灵活实现物理世界中的任意函数映射,彻底摆脱芯片原生指令集的功能限制。




 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







