论文题目:DeepSeekMath_V2
论文地址:https://github.com/deepseek-ai/DeepSeek-Math-V2/blob/main/DeepSeekMath_V2.pdf
发表时间与平台:GitHub,2025年11月
所属机构:DeepSeek
研究背景与动机(Motivation)
当前,大型语言模型(LLM)在解决数学推理任务时,普遍依赖强化学习(RL),通过判断最终答案的正确性或解题过程的合理性来优化模型。然而,这种方法存在两个显著缺陷:
- 其一,可能存在“答案正确但推导过程错误”的情况,导致逻辑不严谨;
- 其二,难以适用于定理证明等开放性任务,因缺乏明确的参考答案作为监督信号。
因此,现有方法在处理需要高度严谨性的数学推理任务时表现受限,无法满足对严密逻辑验证的需求。
核心贡献
- 构建了一个高精度且忠实可靠的基于LLM的数学证明验证器;
- 引入元验证机制(Meta-Verification),有效缓解模型幻觉问题,提升验证结果的可信度;
- 激励证明生成器通过自我验证机制不断提升证明质量;
- 扩展验证计算能力,实现对复杂证明的自动标注,在无需人工干预的前提下持续改进验证器性能。
方法设计的关键观察
本研究的方法建立在以下三点人类认知特性的启发之上:
- 人类即使在没有标准解答的情况下,也能识别出证明中的漏洞——这一能力对于应对开放性问题至关重要;
- 当经过充分验证仍未发现错误时,该证明更有可能是有效的;
- 发现并指出问题所需的努力程度,可作为衡量证明质量的有效代理指标,并用于优化生成过程。
验证器的迭代优化机制
验证器被设计为参与一个闭环式的持续改进流程:
- 利用验证反馈信息优化证明生成策略;
- 增强验证计算资源,自动识别并标记难以验证的新类型证明,从而生成高质量训练数据以反哺验证器自身;
- 使用升级后的验证器进一步指导和优化证明生成器的表现。
这种机制形成了“左脚踩右脚”式的自举式提升路径。更重要的是,一个可靠的验证器使得证明生成器能够学会像验证器一样评估自己的输出,进而实现对证明的反复修正,直到无法再检测到新问题为止。本质上,模型被赋予了对奖励函数的显式理解,使其可以通过深思熟虑的推理而非盲目试错来最大化收益。
证明验证器的设计细节
评分标准
验证器采用三级评分体系对证明进行打分:
- 1分:证明完整且逻辑严谨,所有步骤均有清晰依据;
- 0.5分:整体逻辑成立,但存在轻微错误或细节缺失;
- 0分:证明包含根本性逻辑错误或关键漏洞,无法成立。

数据集构建
从 Art of Problem Solving (AoPS) 平台收集约17,000道数学问题,使用 DeepSeek-V3.2-Exp-Thinking 模型生成初步解答,并由人工按照上述标准进行0、0.5或1分的标注。
强化学习中的奖励设计
在训练过程中,验证器的奖励由两部分组成:
- R_format:格式合规性得分;
- R_score:预测分数与真实人工评分之间的差异惩罚项。
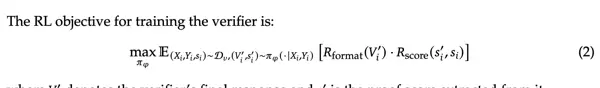
挑战与改进:引入元验证机制
初期发现,验证器在面对错误证明时,可能虚构“问题原因”以获得高分奖励,即出现“虚假诊断”现象。为此,研究引入元验证器(Meta-Verifier),对原始验证器的判断进行二次校验,形成双重验证机制。实验表明,加入元验证后,验证器的整体准确率从0.85显著提升至0.96。

证明生成器的设计与激励机制
设 Y 为证明生成器输出的证明,其对应预估得分为 R_Y = s;Z 为生成器内部进行的自我分析(可视作前置验证,Pre-verification),其得分为 R_Z = s'。整体奖励函数设计如下:
- s 与 s' 的差值:鼓励模型诚实地承认自身错误,若自我评估与实际评分一致则加分,反之谎报严谨性将受罚;
- R_Y + R_Z:最高奖励授予那些既能生成正确证明又能准确评估其质量的模型;
- R_meta(Z):鼓励模型在最终输出前尽可能多地发现并修复潜在问题。
总体目标是让模型不仅具备解题能力,还能主动反思、识别缺陷并如实报告。三者关系可类比为:会自省的学生 → 老师 → 督导,构成一个内外结合、层层把关的认知架构。

验证器与生成器的协同进化:自动化数据扩展
通过多轮验证与元验证过程,采用多数投票策略判定证明是否达到1分标准,或所提出的问题是否合理有效。该机制实现了训练数据的自动化扩展,减少了对外部人工标注的依赖,推动系统在封闭环境中实现自我增强。
实验设置与评测数据集
为全面评估模型性能,研究采用了多个权威数学竞赛数据集:
- IMO 2025(6题):国际数学奥林匹克竞赛,面向中学生的世界顶级赛事;
- CMO 2024(6题):中国数学奥林匹克全国决赛;
- Putnam 2024(12题):北美最具影响力的本科生数学竞赛;
- ISL 2024(31题):IMO候选试题库,涵盖广泛难度与题型;
- IMO-ProofBench(60题):由DeepMind构建,分为基础组(30题,覆盖IMO简单至中等难度)和高级组(30题,模拟完整IMO考试,最高达IMO最难级别)。
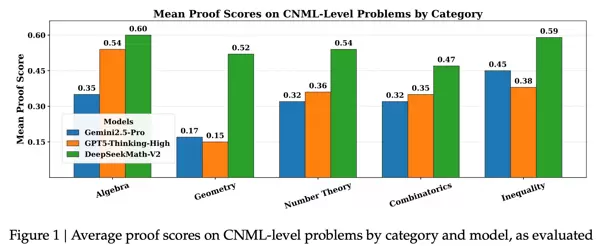
单次生成性能对比
在多项基准测试中,DeepSeekMath-V2 在单次生成场景下表现优于 GPT-5-Thinking-High 和 Gemini 2.5-Pro,展现出更强的首次推理准确性与逻辑完整性。
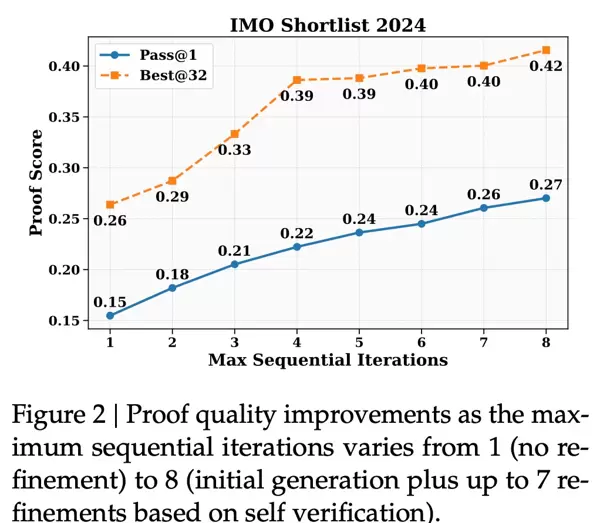
多次生成策略的效果
进一步实验表明,结合自我验证与迭代重生成机制,模型可通过多次尝试不断优化输出证明,显著提高最终通过验证的比例,体现出强大的自我修正能力。
由于面对的是较为复杂的难题,128K的token容量难以一次性完成完整解答,因此采用了多轮评估的方式,逐步优化和补充证明过程。随着迭代推进,评估得分也呈现出持续上升的趋势。
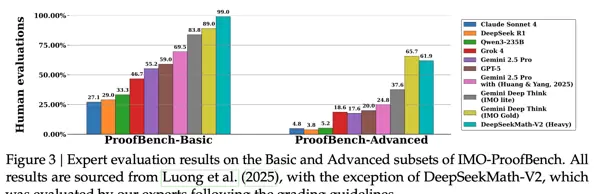
在IMO竞赛中已具备获得金牌的实力与水平。

参考文献:
- https://mp.weixin.qq.com/s/FctcBGr76_geN0FAVjXWQQ
以上内容基于个人理解撰写,若存在疏漏或错误,欢迎批评指正。




 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







