Fourier Basis Mapping: A Time-Frequency Learning Framework for Time Series Forecasting
研究背景
在时间序列分析中,傅里叶变换被广泛用于将信号从时域转换到频域,使模型能够从频率维度提取特征。然而,当前基于傅里叶变换的方法面临两个关键挑战:
- 起始周期不一致问题:傅里叶变换的实部和虚部分别对应余弦和正弦基函数的系数,单独处理这些分量而忽略其对应的基函数,会导致频率成分缺乏明确的物理解释;
- 序列长度依赖性问题:频率的定义依赖于输入序列的长度,不同长度下相同频率的实际含义可能不同,且传统方法往往忽视了时间信息,难以精确建模时频关系。
为解决上述问题,本文提出傅里叶基映射(FBM),通过引入傅里叶基函数展开与时空映射机制,融合时域与频域特征,实现对频率成分的清晰解释并保留时间结构特性。该方法具备“即插即用”能力,仅需替换或调整神经网络的初始投影层即可集成至多种架构,显著提升预测性能。

核心思路解析
傅里叶变换中的实部 $ H_R $ 和虚部 $ H_I $ 实质上是不同频率下余弦和正弦基函数的加权系数。现有方法通常直接操作频谱,未考虑基函数本身的时间结构,导致:
- 无法建立不同起始相位序列之间的可解释映射;
- 当输入长度不能被频率整除时,基函数表现出时间依赖性,缺失基函数建模会削弱模型对频率成分的理解能力。
而 FBM 明确引入正交余弦基 $ C $ 和正弦基 $ S $,将频谱系数与对应基函数相乘后叠加,重构出具有时间语义的时频表示:
$$ X_{\text{reconstruct}} = H_R \cdot C + H_I \cdot S $$这一过程不仅恢复了时间动态,还增强了频率特征的可解释性。因此,FBM 在统一的时频空间中进行建模,而非局限于单一的时间或频率空间。
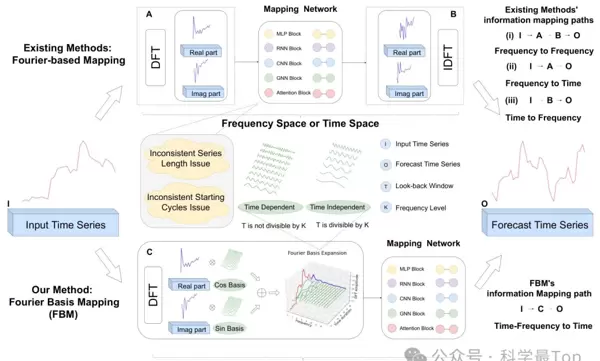
实例分析:揭示现有方法的局限性
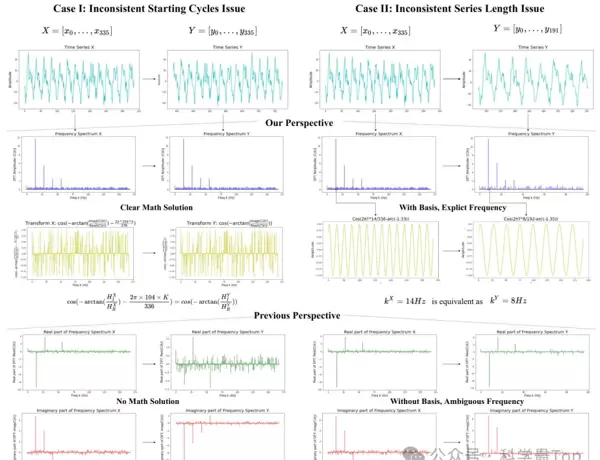
图2展示了两种典型场景,说明传统方法在面对周期偏移和长度变化时的不足。
Case I:相同频率与长度,但起始周期不同
对于两个同频同长但起始相位不同的序列 X 和 Y,其频谱幅值相近但相位不同。传统方法因缺乏基函数支持,难以建立两者间的数学映射关系。而 FBM 利用振幅与反正切相位信息,结合基函数可准确还原时间模式,实现有效对齐。
Case II:相同频率与起始点,但序列长度不同
以8Hz余弦信号为例,在不同长度序列中其实际波形覆盖周期数不同,导致物理意义发生变化。传统频域方法无法捕捉这种差异,而 FBM 引入的时间相关基函数能自适应地反映长度变化带来的影响,从而更精准建模频率行为。
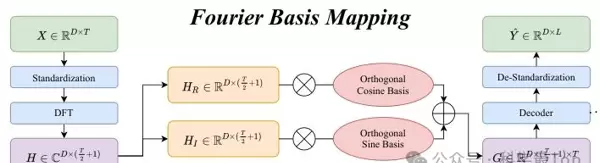
方法设计:FBM 架构详解
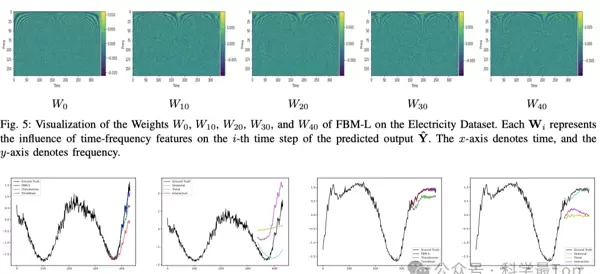
图3展示了傅里叶基映射(FBM)的整体网络结构。其核心思想是通过基函数重构生成富含时间信息的时频特征,具体实现方式如下:
- 将频率谱的实部 $ H_R $ 与正交余弦基 $ C $ 相乘;
- 将虚部 $ H_I $ 与正交正弦基 $ S $ 相乘;
- 将二者结果相加,得到最终的时频表示。
该表示既保留了原始频率成分的结构,又嵌入了时间位置信息,使得下游任务可在更丰富的时频空间中进行预测,解决了传统频域映射中存在的歧义性和不可逆问题。
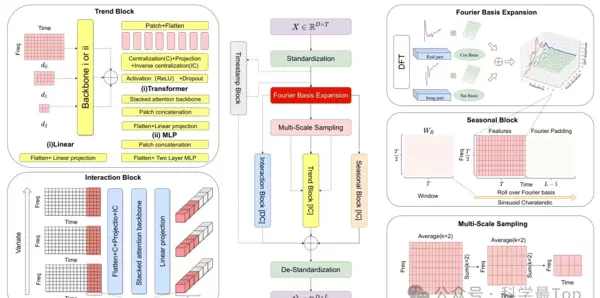
协同框架 FBM-S 的模块化设计
图4展示的是本文提出的完整预测框架 FBM-S,由三个功能模块组成,分别处理趋势、季节性及交互效应,并采用 ID(独立通道)与 DC(依赖通道)建模相结合的方式,兼顾局部与全局特征关联。
1. 季节性模块
专注于捕捉周期性模式。通过对扩展后的傅里叶基应用滚动窗口机制,充分利用正弦/余弦基函数的周期性质,高效识别多尺度季节成分。
2. 趋势模块
灵活支持线性模型、MLP 或 Transformer 等多种架构,用于建模非线性长期趋势。同时引入以下关键技术:
- 分块处理:基于时频特征的时间片段划分,增强局部建模能力;
- 中心化与逆中心化:在初始投影前后进行均值归一化与还原,优化特征分布;
- 多尺度下采样:结合平均核与求和核,提升模型对不同分辨率数据的适应性。
3. 交互模块
针对短期动态变化中的复杂交互行为,设计了掩码机制,用于建模输入与输出序列长度之间的依赖关系,过滤无关上下文信息。此外,引入中心化技术增强特征鲁棒性,有助于识别峰值、谷值等关键状态。
ID 与 DC 的结合策略使模型既能独立建模各变量特性,又能捕捉跨通道依赖,全面提升预测精度。
实验评估与结果分析
本文在12个真实世界时间序列数据集上进行了全面实验,涵盖长期与短期预测任务。对比方法包括六类主流模型:线性方法、基于Transformer、MLP、RNNs、CNNs以及傅里叶相关方法。
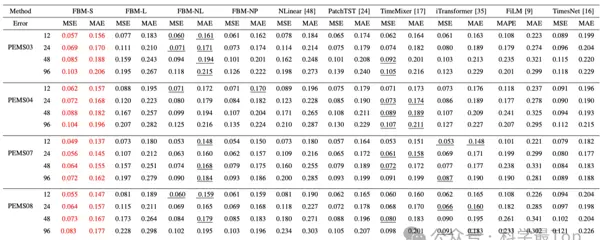
评估指标采用 MSE 和 MAE,测试 FBM 的多个变体(FBM-L、FBM-NL、FBM-NP)以及整体框架 FBM-S 的表现。实验结果显示:
- FBM 系列模型在大多数数据集上优于基线方法;
- FBM-S 表现尤为突出,验证了模块协同的有效性;
- 效率分析表明模型计算开销可控,具备实际部署潜力;
- 消融研究证实各组件(如基函数映射、中心化、多尺度采样等)均对性能有显著贡献。
综上所述,FBM 提供了一种新颖且高效的时频联合学习范式,通过显式引入傅里叶基函数,解决了传统频域方法在时间一致性与可解释性方面的缺陷,为时间序列预测提供了新的建模范式。





 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







