监督学习核心概念（Supervised Learning）

是 否 +2 论坛币

k人 参与回答

经管之家送您一份

应届毕业生专属福利!

求职就业群

赵安豆老师微信：zhaoandou666

经管之家联合CDA

送您一个全额奖学金名额~ !

立即领取

感谢您参与论坛问题回答

经管之家送您两个论坛币！

+2 论坛币

监督学习的基本原理与核心框架

监督学习是机器学习中最为基础和广泛应用的一类方法，其目标是从带有标签的训练数据中学习一个模型，使得该模型能够对未知样本做出准确预测。整个过程可归纳为三个关键组成部分：模型、策略与算法。

方法 = 模型 + 策略 + 算法

最终追求的是具备良好泛化能力的模型——即在未见数据上依然表现优异的模型。

1. 假设空间与模型形式

在监督学习中，所有可能的映射函数或条件概率分布构成的空间被称为假设空间（Hypothesis Space）。这个空间限定了我们寻找最优模型的范围。

1.1 模型的两种基本表达方式

模型可以分为两类主要形式：决策函数模型和条件概率模型，每种均可进一步表示为参数化形式。

模型类型	一般形式	参数化形式
决策函数模型	= {f ∣ Y = f(x)}	= {f ∣ Y = f_θ(x), θ ∈ }
条件概率模型	= {P ∣ P(Y|x)}	= {P ∣ P_θ(Y|x), θ ∈ }

其中，θ 表示模型的参数向量， 表示 n 维实数空间，代表参数的取值范围。

2. 学习策略：损失函数与风险最小化原则

学习策略的核心在于定义如何评估预测结果的好坏，并据此选择最优模型。这通常通过构建损失函数并最小化相应的风险函数来实现。

2.1 损失函数（Loss Function）

损失函数用于衡量单次预测的误差大小，记作 L(Y, f(x)) 或 L(Y, P(Y|x))，具体形式依据任务类型而定：

• 0-1 损失函数（适用于分类任务）：
  L(Y, f(x)) = {

  1,	Y ≠ f(x)
  0,	Y = f(x)

  }
• 平方损失函数（常用于回归问题）：
  L(Y, f(x)) = (Y f(x))
• 绝对损失函数（稳健回归）：
  L(Y, f(x)) = |Y f(x)|
• 对数损失函数（用于概率输出模型）：
  L(Y, P(Y|x)) = logP(Y|x)

总体而言，损失值越低，说明模型对该样本的预测效果越好。

2.2 风险函数（Risk Function）

风险函数是对期望损失的度量，反映模型在整个输入-输出联合分布上的平均表现：

R_exp(f) = [L(Y, f(X))] = ∫ L(y, f(x))P(x,y)dxdy

由于真实分布未知，无法直接计算期望风险，因此引入经验风险作为替代估计。

2.3 风险最小化准则

为了从数据中选出最优模型，常用以下两种最小化准则：

1. 经验风险最小化（Empirical Risk Minimization, ERM）
   使用训练集上的平均损失近似期望风险：
   R_emp(f) = (1/N) Σ L(y, f(x))
   适用于样本量充足的情况。
2. 结构风险最小化（Structural Risk Minimization, SRM）
   在经验风险基础上加入正则项，防止模型过于复杂导致过拟合：
   R_srm(f) = R_emp(f) + λ·J(f)
   适合小样本场景，有助于提升泛化性能。

2.4 训练误差与测试误差分析

• 训练误差（Training Error）：模型在训练集上的平均损失，反映拟合程度。
• 测试误差（Test Error）：模型在独立测试集上的损失，体现泛化能力。

理想情况下两者应接近；若训练误差很低但测试误差很高，则表明出现过拟合现象。

2.5 过拟合与正则化机制（以多项式回归为例）

以多项式回归为例，探讨过拟合的发生机理及缓解手段。

1. M 次多项式模型（M-th Order Polynomial Model）
   设模型形式为：f_θ(x) = θ + θx + θx + … + θ_M x^M
   当 M 过大时，模型可能过度拟合噪声，丧失泛化能力。
2. 经验风险最小化（无正则化）：过拟合的根源之一
   单纯最小化训练误差可能导致模型复杂度过高，完美拟合训练数据却在新数据上失效。
3. 正则化：控制模型复杂度的关键手段
   通过对参数施加惩罚项，限制模型自由度，从而抑制过拟合。

① L2 正则化（岭回归）

添加参数平方和作为惩罚项：
R_srm = R_emp + λ‖θ‖

② L1 正则化（Lasso 回归）

使用参数绝对值之和进行约束：
R_srm = R_emp + λ‖θ‖

L1 能促使部分系数变为零，具有特征选择功能；L2 则更倾向于均匀压缩参数。

核心对比与总结

方法	优点	缺点
ERM（经验风险最小化）	简单直观，大数据下有效	易导致过拟合，尤其在小样本时
SRM（结构风险最小化）	兼顾拟合与泛化，抗过拟合能力强	需调节正则系数 λ，增加调参成本

3. 泛化误差及其上界理论

3.1 泛化误差（Generalization Error）

泛化误差是指模型在真实数据分布下的期望损失，即：

R(f) = _{X,Y}[L(Y, f(X))]

它是衡量模型真正性能的标准，但由于真实分布未知，只能通过测试误差进行估计。

3.2 泛化误差上界（Generalization Error Bound）

在有限样本条件下，可通过统计学习理论推导出泛化误差的上界，揭示模型复杂度与样本数量之间的关系。

二分类问题中的泛化误差上界

对于二分类任务，在满足一定条件下，存在如下形式的泛化误差边界：

R(f) ≤ R_emp(f) + ε(d, N, δ)

其中 d 是模型容量（如VC维），N 是样本数，δ 是置信水平，ε 是与这些因素相关的偏差项。

证明基础：Hoeffding 不等式

Hoeffding 不等式为上述边界的推导提供了数学支撑。它指出：对于独立有界随机变量，其样本均值偏离真实期望的概率呈指数衰减。

基于此，可以证明当样本量足够大时，经验风险将趋近于期望风险，从而保证学习过程的有效性。

监督学习的整体流程与设计原则

• 确定模型类型：选择合适的函数族，如线性模型、神经网络等。
• 设定损失函数：根据任务性质选用 0-1 损失（分类）、平方损失（回归）或对数损失（概率建模）。
• 制定学习策略：
  • 数据丰富 → 采用经验风险最小化（ERM）
  • 数据稀缺 → 引入正则化，实施结构风险最小化（SRM）
• 评估模型性能：结合训练误差（看拟合程度）与测试误差（看泛化能力），警惕过拟合。
• 保障泛化能力：增加样本量、简化模型结构，均可降低泛化误差。
• 最终决策：选取结构风险最小的模型作为最终输出。

综上所述，监督学习的本质是在偏差与方差之间寻求平衡，通过合理建模与正则化手段，获得既拟合良好又具备强泛化能力的预测系统。

在机器学习中，评估模型性能的一个核心任务是衡量其预测的准确性。这通常通过风险的概念来形式化描述，主要包括期望风险、经验风险以及结构风险等不同层面。

期望风险（Expected Risk）
期望风险是从理论上刻画模型在整个数据分布上的平均损失情况。给定输入输出的联合概率分布 $ P(x, y) $，模型 $ f $ 的期望风险定义为：

$$ \mathcal{R}_{exp}(f) = \mathbb{E}_P[L(Y,f(x))] = \int_{X \times Y} L(Y,f(x)) P(x,y)\,dx\,dy $$

该值反映了模型在真实数据分布下的整体表现。理想情况下，我们希望选择使期望风险最小的函数作为最优模型。但由于真实分布 $ P(x, y) $ 通常是未知的，因此无法直接计算期望风险。

经验风险（Empirical Risk）
由于无法获取完整的数据分布，实践中常用训练集上的平均损失来近似期望风险，即经验风险：

$$ \mathcal{R}_{emp}(f) = \frac{1}{N} \sum_{i=1}^N L(y_i, f(x_i)) $$

当样本数量 $ N \to \infty $ 时，根据大数定律，经验风险会收敛于期望风险。然而在实际应用中，样本量有限，单纯最小化经验风险可能导致模型过度拟合训练数据，从而在新样本上泛化能力下降。

风险最小化准则

（1）经验风险最小化（ERM）
经验风险最小化原则认为：在假设空间 $ \mathcal{F} $ 中选择使经验风险最小的模型是最优策略。其优化目标为：

$$ \min_{f \in \mathcal{F}} \frac{1}{N} \sum_{i=1}^N L(y_i, f(x_i)) $$

这一方法适用于训练样本足够大的情形。但在小样本条件下，容易引发过拟合问题，因为模型可能会记住噪声或特例而失去泛化能力。

（2）结构风险最小化（SRM）
为了缓解过拟合现象，结构风险最小化引入了对模型复杂度的惩罚机制，相当于正则化的思想。结构风险的表达式如下：

$$ \mathcal{R}_{srm}(f) = \frac{1}{N} \sum_{i=1}^N L(y_i, f(x_i)) + \lambda J(f) $$

其中 $ J(f) $ 表示模型复杂度的度量（如权重的范数），$ \lambda \geq 0 $ 是控制正则化强度的超参数，用于平衡拟合精度与模型简洁性之间的关系。SRM 的优化目标是寻找使结构风险最小的模型：

$$ \min_{f \in \mathcal{F}} \frac{1}{N} \sum_{i=1}^N L(y_i, f(x_i)) + \lambda J(f) $$

这种方法在样本较少时尤为有效，能够提升模型的泛化性能。

[此处为图片3]

训练误差与测试误差

（1）训练误差（Training Error）
训练误差是指模型在训练数据集上的平均损失，形式上与经验风险一致：

$$ \mathcal{R}_{emp}(\hat{f}) = \frac{1}{N} \sum_{i=1}^N L(y_i, \hat{f}(x_i)) $$

它反映的是模型对已知数据的拟合程度，但不能完全代表其在未知数据上的表现。

（2）测试误差（Test Error）
测试误差衡量的是模型在独立测试集上的表现，定义为：

$$ E_{test} = \frac{1}{N'} \sum_{i=1}^{N'} L(y_i, \hat{f}(x_i)) $$

若采用 0-1 损失函数（分类任务中常见），则测试误差可写为：

$$ E_{test} = \frac{1}{N'} \sum_{i=1}^{N'} I(y_i \neq \hat{f}(x_i)) $$

相应的，测试准确率为：

$$ r_{test} = \frac{1}{N'} \sum_{i=1}^{N'} I(y_i = \hat{f}(x_i)) $$

测试误差更能体现模型的真实泛化能力，是模型选择的重要依据。

[此处为图片4]

过拟合与正则化实例：多项式回归分析

以 M 次多项式回归为例说明过拟合和正则化的作用。设模型形式为：

$$ f_M(x, w) = w_0 + w_1 x + w_2 x^2 + \cdots + w_M x^M $$

随着多项式阶数 $ M $ 增加，模型复杂度上升，可能完美拟合训练数据点，包括其中的噪声。此时虽然训练误差极低，但测试误差反而升高，表现出明显的过拟合现象。

通过引入正则化项（如 L2 正则），限制系数大小，可以有效抑制高阶项的影响，降低模型复杂度，从而改善泛化性能。这也体现了结构风险最小化在实践中的价值。

在多项式回归中，模型的预测函数通常表示为：

f_M(x,w) = w_0 + w_1x + w_2x^2 + \dots + w_Mx^M = \sum_{i=0}^M w_i x^i

其对应的参数化形式可写作：

f_M^*(x, w) = w_0^* + w_1^*x + w_2^*x^2 + \dots + w_M^*x^M = \sum_{i=0}^M w_i^* x^i

符号	含义	示例说明
M	多项式阶数（反映模型复杂度）	M=0 表示常数函数；M=1 对应线性模型（直线）；M=9 则为高阶曲线，拟合能力更强但易过拟合
w_i	多项式各项的系数（即待学习的模型参数）	w_0 为截距项，w_1 为一次项系数，这些参数需通过训练数据进行优化求解
f_M(x, w)	模型对输入 x 的预测输出值	目标是使该预测值尽可能接近真实标签 y，实现良好拟合

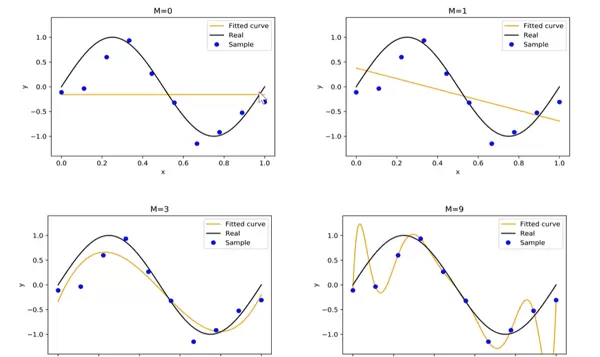
上图对比了不同阶数 M 下的拟合曲线表现，揭示出以下规律：

• M=0（常数函数）：表现为一条水平直线，完全无法捕捉数据的变化趋势，属于典型的欠拟合现象，说明模型复杂度过低。
• M=1（一次函数）：呈现为斜线，虽能反映大致上升或下降趋势，但仍无法适应非线性变化，仍处于欠拟合状态。
• M=3（三次多项式）：拟合曲线与真实趋势（通常以黑色实线表示）高度一致，既贴合数据又保持平滑，表现出良好的泛化性能，为理想情况。
• M=9（九次多项式）：虽然精确穿过所有训练样本点，但在区间内出现剧烈震荡，严重偏离真实函数走势，这是典型的过拟合——模型过度记忆噪声而非学习规律。

总体来看：

• 当 M 较小时，模型结构简单，容易发生欠拟合（拟合能力不足）；
• 随着 M 增大，模型复杂度提升，逐渐具备更强的表达能力，但也更易陷入过拟合；
• 最优策略是选择适中的 M 值，或引入正则化机制（如 L1/L2 正则），限制高阶项的影响，从而在拟合能力和泛化能力之间取得平衡。

经验风险最小化（无正则化）：过拟合的关键诱因之一

在平方误差损失下，经验风险函数定义如下：

L(w) = \frac{1}{2} \sum_{i=0}^N \left( \sum_{j=0}^M w_j x_i^j - y_i \right)^2

此公式代表无正则化条件下的优化目标，旨在最小化模型在训练集上的整体预测误差。其中：

• 系数 \frac{1}{2} 主要用于简化后续求导运算，不影响最优解的位置；
• 内部求和项 \sum_{j=0}^M w_j x_i^j 表示模型对第 i 个样本的预测结果；
• 与真实值 y_i 的差值被平方后累加，构成总损失。

问题在于：当 M 过大（例如 M=9）时，模型拥有极强的自由度，为了将训练误差降至最低，算法会不断调整参数 w_j，甚至使其取值极大，导致拟合曲线产生不必要的波动。这正是“高复杂度模型在缺乏约束时必然过拟合”的根本原因。

正则化：控制模型复杂度、防止过拟合的核心手段

正则化的思想是在原始损失函数基础上增加一个“复杂度惩罚项”，使得优化过程不仅关注误差最小化，也兼顾模型简洁性。常见的两种方法如下：

① L2 正则化（岭回归）

损失函数扩展为：

L(w) = \frac{1}{N} \sum_{i=1}^N (f(x_i;w)-y_i)^2 + \frac{\lambda}{2} \|w\|_2^2

其中 \|w\|_2^2 = \sum_j w_j^2，表示所有权重参数的平方和。

• 作用机制：通过对所有参数施加平方惩罚，迫使高阶项系数趋向于较小值，从而让曲线更加平滑；
• 特点：不会将系数完全压缩至零，而是整体缩小，保留全部特征；
• 调节参数 λ：λ 越大，惩罚力度越强，模型越趋于简单；若 λ 过大，则可能导致欠拟合。

② L1 正则化（Lasso 回归）

其形式为：

L(w) = \frac{1}{N} \sum_{i=1}^N (f(x_i;w)-y_i)^2 + \lambda \|w\|_1

其中 \|w\|_1 = \sum_j |w_j|，即所有参数绝对值之和。

• 作用机制：除压缩参数外，L1 正则还能促使部分不重要特征的系数变为零；
• 核心优势：实现自动特征选择，有效降低模型维度，特别适用于冗余特征较多的情形；
• 效果体现：得到稀疏解，提升模型可解释性。

两类正则化方法对比总结

正则化类型	惩罚形式	主要效果	适用场景
L2（岭回归）	参数平方和（\|w\|_2^2）	参数整体缩小，曲线更平滑	希望保留全部变量，仅抑制过拟合
L1（Lasso）	参数绝对值和（\|w\|_1）	产生稀疏解，部分系数归零	需要特征筛选、简化模型结构

关键要点总结

• 当 λ = 0 时，等同于未使用正则化，模型易出现过拟合；
• 当 λ 过大时，模型受到过度压制，可能无法充分拟合数据，导致欠拟合；
• 最佳 λ 值需通过交叉验证、验证集评估等方式确定，以实现偏差与方差的最佳权衡。

综上所述，过拟合（Over-Fitting）的本质是模型过于复杂，过度适应训练数据中的噪声与细节，丧失对新数据的泛化能力。通过合理选择模型复杂度并结合正则化技术，可以有效缓解这一问题，提升模型的实际应用价值。

在监督学习中，过拟合是一个普遍存在的挑战。其本质是指模型参数过多，导致模型对已知的训练数据预测效果极佳，甚至能够完美拟合，但在面对未知的新数据时表现显著下降。

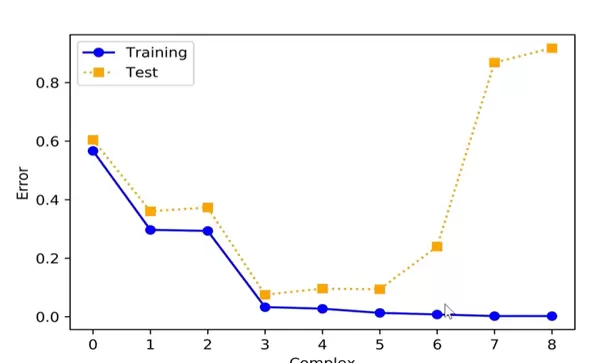
通过以下图表可以更清晰地理解这一现象（横轴表示模型复杂度，纵轴为误差）：

图表分析如下：

• 蓝色曲线（训练误差）：随着模型复杂度的增加，训练误差持续降低，最终可能趋近于零，说明模型已经“记住”了训练集中的每一个细节；
• 黄色曲线（测试误差）：当模型复杂度较低时，测试误差与训练误差同步下降；但一旦复杂度超过某一临界点，测试误差反而迅速上升，表明模型失去了对新样本的泛化能力。

造成这种现象的根本原因在于：当模型过于复杂时，它不仅学习到了数据背后的潜在规律，还过度捕捉了训练数据中的噪声和随机波动，从而削弱了其推广到新数据上的能力。

3. 泛化误差及其上界理论

3.1 泛化误差（Generalization Error）

泛化误差指的是模型在未见过的数据上的期望风险，是评估模型泛化性能的核心指标。数学表达式如下：

\(\mathcal{R}_{exp}(\hat{f}) = \mathbb{E}_P[L(Y,\hat{f}(x))] = \int_{X \times Y} L(y,\hat{f}(x)) P(x,y)dxdy\)

3.2 泛化误差上界（Generalization Error Bound）

该上界用于刻画经验风险与真实期望风险之间的差距，提供了一个概率意义上的误差边界。

针对二分类问题的泛化误差上界分析：

前提条件设定：

• 给定训练集 \(T = \{(x_1,y_1),(x_2,y_2),\dots,(x_N,y_N)\}\)，其中样本数量为 \(N\)，且所有样本独立同分布于联合分布 \(P(X,Y)\)；
• 输入空间 \(X \in \mathbb{R}^n\)，输出标签 \(Y \in \{-1,+1\}\)，采用0-1损失函数；
• 假设空间为有限集合 \(\mathcal{F}=\{f_1,f_2,\dots,f_d\}\)，共包含 \(d\) 个候选模型函数。

核心结论：

对于任意模型 \(f \in \mathcal{F}\)，至少以概率 \(1-\delta\)（其中 \(0 < \delta < 1\)）满足以下不等式：

\(\mathcal{R}(f) \leq \hat{\mathcal{R}}(f) + \varepsilon(d,N,\delta)\)

其中，误差项定义为：

\(\varepsilon(d,N,\delta) = \sqrt{\frac{1}{2N} \left( \log d + \log \frac{1}{\delta} \right)}\)

结论解析：

• 泛化误差由两部分构成：经验风险 \(\hat{\mathcal{R}}(f)\) 和一个与模型复杂度相关的修正项 \(\varepsilon\)；
• \(\varepsilon\) 随样本量 \(N\) 增大而减小，说明更多数据有助于缩小泛化误差；
• \(\varepsilon\) 与 \(\sqrt{\log d}\) 成正比，意味着假设空间越庞大（即候选模型越多），上界越大，泛化能力越难保证。

理论支撑：Hoeffding 不等式

该结论的证明依赖于 Hoeffding 不等式，形式如下：

\(P[\bar{X}-\mathbb{E}(\bar{X}) \geq t] \leq \exp \left( -\frac{2N^2 t^2}{\sum_{i=1}^n (b_i - a_i)^2} \right)\)

关键推导步骤：

• 令单个样本损失 \(X_i = L(y_i,f(x_i))\)，则样本平均损失 \(\bar{X} = \hat{\mathcal{R}}(f)\)，其期望 \(\mathbb{E}(\bar{X}) = \mathcal{R}(f)\)；
• 由于使用的是0-1损失，故 \(X_i \in [0,1]\)，满足Hoeffding条件；
• 代入后可得：\(P(\mathcal{R}(f) - \hat{\mathcal{R}}(f) \geq \varepsilon) \leq \exp(-2N\varepsilon^2)\)。

由此建立了经验风险与真实风险之间的概率联系，为泛化误差上界的推导提供了基础。

对假设空间中的所有函数应用联合界（Union Bound），可得不等式：

\[ P(\mathcal{R}(f) - \hat{\mathcal{R}}(f) \geq \varepsilon) \leq \exp(-2N\varepsilon^2) \]

进一步考虑整个函数空间的复杂度，引入假设空间大小相关的因子 \( d \)，令置信水平参数满足：

\[ \delta = d \exp(-2N\varepsilon^2) \]

对该式进行变换，解出误差界限 \( \varepsilon \)，得到：

\[ \varepsilon = \sqrt{\frac{1}{2N} \left( \log d + \log \frac{1}{\delta} \right)} \]

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

分享0 收藏0 回帖

关键词：Learning earning super Learn supe