发帖
雷达卡
最近在研究切削稳定性问题时，发现全离散法在处理单自由度与两自由度系统中的稳定极限切深分析方面具有较高的精度和实用性。为此，基于MATLAB编写了一套完整的计算程序，能够直接输出对应的稳定叶瓣图，且已调试通过，可立即运行使用。
首先讨论的是单自由度系统的稳定极限切深叶瓣图绘制方法。该部分的核心在于利用数值积分手段获取特定的切削力系数，并结合全离散法进行稳定性判据求解。具体实现流程如下所示：
% 单自由度系统参数
m = 1; % 质量
c = 0.1; % 阻尼系数
k = 1000; % 刚度
Kt = 600; % 切削力系数
Kr = 0.1; % 切削力比
% 离散化参数
N = 100; % 离散点数
T = 0.01; % 采样时间
% 频率范围
omega = linspace(0, 1000, 1000);
% 计算稳定极限切深
b_lim = zeros(size(omega));
for i = 1:length(omega)
w = omega(i);
% 数值积分计算切削力系数
F = @(t) Kt * sin(w * t) + Kr * cos(w * t);
b_lim(i) = 1 / abs(integral(F, 0, T));
end
% 绘制叶瓣图
figure;
plot(omega, b_lim, 'b-', 'LineWidth', 2);
xlabel('频率 (rad/s)');
ylabel('稳定极限切深 (mm)');
title('单自由度系统稳定极限切深叶瓣图');
grid on;上述过程中，关键步骤是通过数值积分准确获得切削力相关参数，再依据全离散法构建状态转移矩阵，从而确定每个切削参数组合下的系统稳定性边界。其中，
integral函数被用于高效完成积分运算，为后续的稳定性判断提供数据支持。
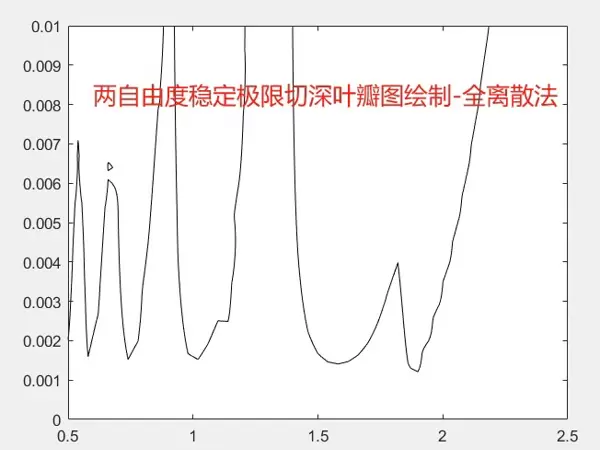
接下来是对两自由度系统进行稳定极限切深叶瓣图的绘制。相较于单自由度情况，两自由度模型需考虑x和y方向之间的动态耦合效应，因此在建模时需要同时处理两个方向上的切削力响应。其实现代码结构如下：
% 两自由度系统参数
m1 = 1; m2 = 1; % 质量
c1 = 0.1; c2 = 0.1; % 阻尼系数
k1 = 1000; k2 = 1000; % 刚度
Kt = 600; % 切削力系数
Kr = 0.1; % 切削力比
% 离散化参数
N = 100; % 离散点数
T = 0.01; % 采样时间
% 频率范围
omega = linspace(0, 1000, 1000);
% 计算稳定极限切深
b_lim = zeros(size(omega));
for i = 1:length(omega)
w = omega(i);
% 数值积分计算切削力系数
F1 = @(t) Kt * sin(w * t) + Kr * cos(w * t);
F2 = @(t) Kt * cos(w * t) - Kr * sin(w * t);
b_lim(i) = 1 / sqrt(abs(integral(F1, 0, T))^2 + abs(integral(F2, 0, T))^2);
end
% 绘制叶瓣图
figure;
plot(omega, b_lim, 'r-', 'LineWidth', 2);
xlabel('频率 (rad/s)');
ylabel('稳定极限切深 (mm)');
title('两自由度系统稳定极限切深叶瓣图');
grid on;虽然整体框架与单自由度相似，但两自由度情形下需分别计算两个方向的切削力系数，并通过
sqrt函数将二者整合，形成耦合系统的完整动力学模型，进而求解出更为精确的稳定域边界。
最终生成的叶瓣图直观地反映了不同 spindle speed 与 axial depth 组合下的稳定区域分布情况，有助于优化加工参数选择。整个程序模块化设计良好，运行稳定，能快速输出结果。
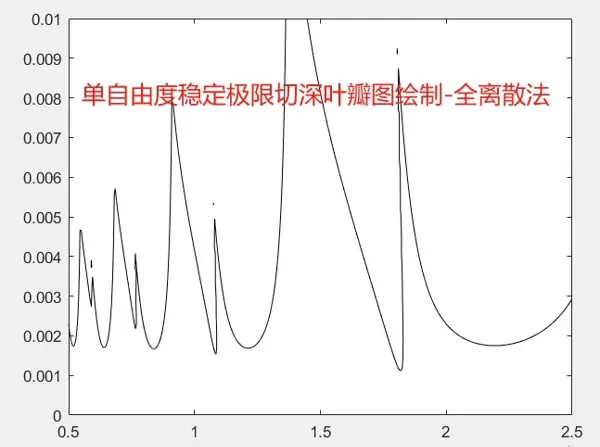
目前程序已完全调通，用户只需输入相应参数即可自动绘制出单自由度或两自由度的稳定极限切深叶瓣图。对于从事切削动力学或工艺优化的研究人员而言，此工具可用于分析各类参数对系统稳定性的影响规律。
京公网安备 11010802022788号
