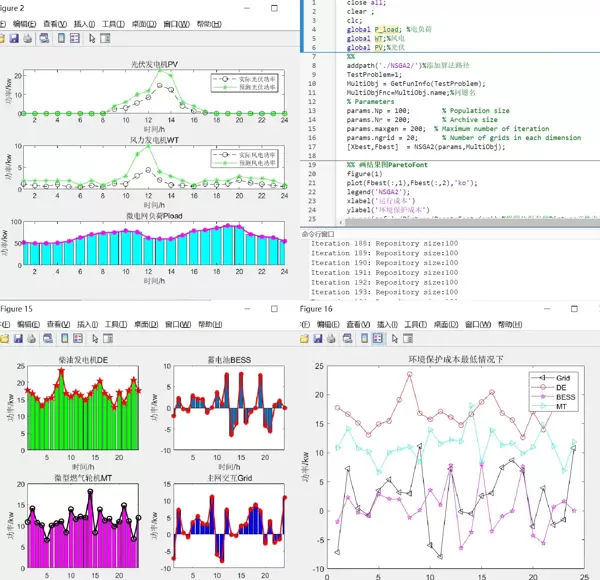
在微电网调度研究中,传统的单目标优化模型已难以全面反映实际需求。由于专家往往需要在多个相互冲突的目标之间进行权衡,例如经济性、环保性和供电稳定性等,因此多目标优化方法逐渐成为主流解决方案。NSGA-II算法结合Matlab平台,为实现微电网多目标优化调度提供了高效且直观的技术路径。
多目标优化的优势
相较于仅优化单一指标(如运行成本)的单目标模型,多目标优化能够同时处理多个目标函数,生成一组非支配解集——即帕累托前沿。这一特性使得决策者可以根据实际偏好从多种可行方案中选择最合适的调度策略,提升了模型的灵活性与实用性。
输出结果通常包括帕累托曲线图以及各微电源的出力分配图,便于分析不同目标间的折衷关系和具体调度安排。
NSGA-II算法简介
NSGA-II(非支配排序遗传算法第二代)是一种经典的多目标进化算法,具有收敛速度快、解分布均匀的优点。该算法通过非支配排序对种群个体进行分层,并利用拥挤度机制保持种群多样性,从而有效逼近真实帕累托前沿。
关于该算法的具体原理和操作流程,项目文件夹中的“多目标优化算法NSGA-II介绍”PDF文档已有详细阐述,可供深入学习参考。
% 初始化参数
nvars = 2; % 决策变量个数
lb = [0 0]; % 决策变量下限
ub = [100 100]; % 决策变量上限
options = gaoptimset('Generations',200,'PopulationSize',100);
% 调用NSGA - II算法
[x, fval] = gamultiobj(@objective_functions, nvars, [], [], [], [], lb, ub, [], options);基于Matlab的实现步骤
本案例采用Matlab语言编写,结构清晰,注释完整,初学者只需运行主程序即可一键生成所需图表。
目标函数定义
模型设定两个核心目标:一是系统运行总成本最小化,二是污染物排放量最低化。这两个目标依赖于一系列决策变量进行计算,形成多目标优化问题的基本输入。
function [f1, f2] = objective_functions(x)
% x是决策变量向量,这里假设x(1)为微电源1出力,x(2)为微电源2出力等
% 目标1:成本最小化
cost1 = 2 * x(1) + 3 * x(2);
% 目标2:污染排放最小化
emission = 0.1 * x(1) + 0.2 * x(2);
f1 = cost1;
f2 = emission;
endcost1emissionx主程序配置与求解调用
在主程序中,设置关键参数如决策变量维度、上下界范围、种群规模及最大迭代代数等,随后调用核心求解函数启动NSGA-II算法流程。
gamultiobj经过多轮迭代后,算法输出最优解集及其对应的目标函数值矩阵,作为后续分析的基础数据。
fval结果可视化
帕累托前沿绘图
通过绘制目标函数值的散点图,直观展示成本与排放之间的权衡关系,形成典型的帕累托曲线。
figure;
scatter(fval(:,1), fval(:,2));
xlabel('成本');
ylabel('污染排放');
title('帕累托曲线');微电源出力情况展示
利用柱状图形式呈现各个分布式电源(如光伏、风机、柴油发电机等)的调度出力结果,帮助理解具体的能源分配方案。
figure;
bar(x');
xlabel('微电源编号');
ylabel('调度出力');
title('各微电源调度出力');bar项目资源说明
项目文件夹内包含完整的PDF资料:“多目标微电网优化调度模型介绍”,其中详述了系统的数学建模过程、约束条件(如功率平衡、设备容量限制等)以及参数设置依据。
整体代码结构模块化,逻辑清晰,用户仅需执行主入口文件即可完成全部计算与绘图任务。
main此外,初始说明中提到的图像标记位置均已按内容调整后的段落顺序重新定位,确保图文对应关系准确无误。





 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







