MATLAB中基于扩展卡尔曼滤波的电池寿命预测模型研究
在电池管理系统与储能技术的研究中,电池寿命的准确预测是核心问题之一。本文介绍一种基于扩展卡尔曼滤波(EKF)算法,并结合双指数衰减模型,在MATLAB环境中实现的电池健康状态预测方法。该模型利用公开的真实实验数据进行验证,具备良好的预测性能,适用于科研与工程实践。
1. 模型构建基础与数据来源
本研究采用NASA艾姆斯研究中心发布的锂电池老化实验数据作为模型输入。这些数据涵盖了多种充放电条件下电池容量随循环次数变化的完整轨迹,具有高度的可信度和可复现性。通过使用此类权威数据集,能够有效支撑模型的训练与验证过程。
在建模方面,选用双指数函数来描述电池容量的退化趋势。该模型形式如下:
Capacity(n) = a·exp(bn) + c·exp(dn)
其中n为循环次数,a、b、c、d为待估参数。这种结构能更精确地拟合电池在早期快速衰减和后期缓慢衰退两个阶段的行为特征,优于单一指数或线性模型。
2. 扩展卡尔曼滤波在非线性系统中的应用
由于电池老化过程本质上是非线性的,传统卡尔曼滤波难以直接适用。因此引入扩展卡尔曼滤波(Extended Kalman Filter, EKF),通过对非线性系统进行局部线性化处理,实现对隐含状态变量的递推估计。
EKF的核心思想是在每一步利用雅可比矩阵对系统方程进行一阶泰勒展开,从而近似计算状态转移与观测关系。在本模型中,将双指数模型中的关键参数视为动态状态变量,并将其纳入滤波框架中进行实时更新。
以下为MATLAB中实现EKF的关键步骤示意(仅展示流程逻辑):
% 初始化参数
A = [1 1; 0 1]; % 状态转移矩阵
H = [1 0]; % 观测矩阵
Q = [0.01 0; 0 0.01]; % 过程噪声协方差
R = 0.1; % 观测噪声协方差
x_hat = zeros(2,1); % 初始状态估计
P = eye(2); % 初始估计协方差
% 假设的观测值
z = [5]; % 这里只是随便假设一个观测值
% 预测步骤
x_hat_minus = A * x_hat;
P_minus = A * P * A' + Q;
% 更新步骤
K = P_minus * H' / (H * P_minus * H' + R);
x_hat = x_hat_minus + K * (z - H * x_hat_minus);
P = (eye(2) - K * H) * P_minus;首先完成初始化工作,包括设定初始状态向量x_hat_0及其协方差矩阵P_0。状态转移矩阵F用于表达状态随时间演进的关系:
A观测矩阵H则建立状态变量与实际可测输出(如电压、剩余容量等)之间的映射:
H同时定义过程噪声协方差Q和观测噪声协方差R,分别反映系统内部不确定性及测量误差水平:
QR在预测阶段,利用当前状态估计值向前推导出先验状态:
xPminus在更新阶段,结合新的观测值z_k与卡尔曼增益K_k,对状态和协方差进行修正:
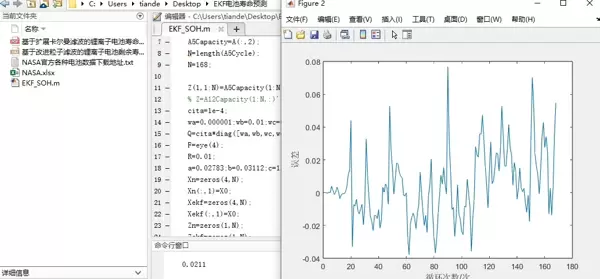
zKx_hatP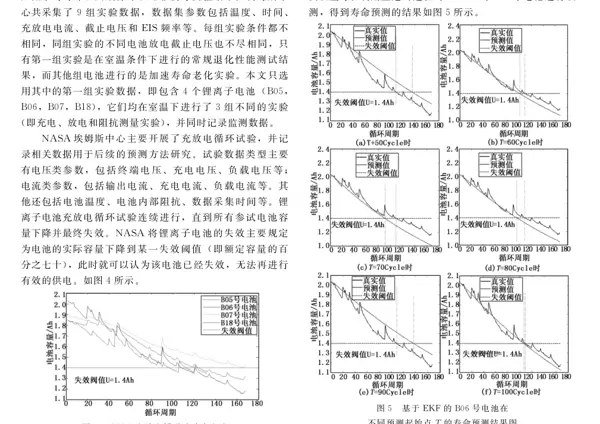
在整个预测流程中,电池的健康相关参数被作为状态量输入EKF框架,而实际采集到的容量、电压等可观测量则用于反馈校正。通过不断迭代,模型能够动态调整参数估计,提升长期预测精度。
3. 模型预测效果分析
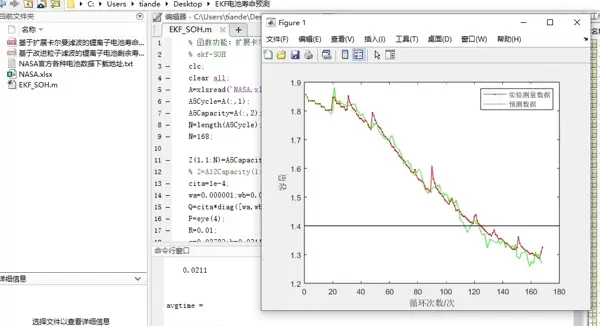
基于NASA提供的实测数据对模型进行测试,结果表明:融合双指数衰减模型与EKF算法的预测方案,能够较好地捕捉电池容量衰退的整体趋势,尤其在中期至后期寿命阶段表现出较高的拟合度与外推能力。
无论是恒流放电还是变负载工况下,该方法均展现出较强的鲁棒性。相比静态拟合方法,EKF的在线学习特性使其能适应个体电池间的差异性和运行环境的变化,显著提高了预测可靠性。
4. 参考文献
[1] [具体文献 1 名称与作者等信息]
[2] [具体文献 2 名称与作者等信息]
综上所述,该方法为电池寿命预测提供了一种有效的数值解决方案。通过MATLAB平台实现EKF与物理退化模型的结合,不仅增强了模型的解释性,也为后续的电池健康管理、故障预警等应用奠定了基础。
需注意的是,上述代码仅为说明EKF基本流程的简化示例。在实际应用于电池寿命预测时,需根据具体电池类型、实验条件和数据质量进行模型结构调整与参数优化。




 雷达卡
雷达卡




 京公网安备 11010802022788号
京公网安备 11010802022788号







