Matlab 基于光流场的交通流量分析与应用

是 否 +2 论坛币

k人 参与回答

经管之家送您一份

应届毕业生专属福利!

求职就业群

赵安豆老师微信：zhaoandou666

经管之家联合CDA

送您一个全额奖学金名额~ !

立即领取

感谢您参与论坛问题回答

经管之家送您两个论坛币！

+2 论坛币

Matlab 实现基于光流场的交通流量分析与运动目标检测

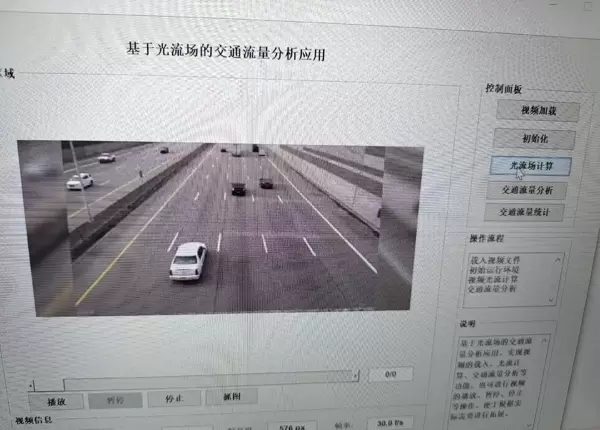
随着智能交通系统的快速发展，对交通流量进行精确监测变得愈发重要。利用光流场技术，可以有效识别视频中的运动目标，如车流或人流，为交通管理提供数据支持。本文将介绍其基本原理，并展示如何使用 Matlab 完成相关算法实现。

光流法的基本原理

光流描述的是图像序列中像素点在时间维度上的运动变化，可理解为“亮度模式的流动”。它能够反映场景中物体的运动方向和速度。通过分析连续帧之间的光流分布，即可判断出哪些区域存在运动目标。

光流方法依赖一个核心假设：在短时间内，图像中某一点的灰度值保持不变。设图像在时刻 $t$ 的亮度为 $I(x, y, t)$，经过微小时间 $\Delta t$ 后，该点移动至 $(x + \Delta x, y + \Delta y)$，则有：

\[ I(x, y, t) = I(x + \Delta x, y + \Delta y, t + \Delta t) \]

对该式进行泰勒展开并忽略高阶项，整理后可得光流的基本约束方程：

\[ \frac{\partial I}{\partial x}u + \frac{\partial I}{\partial y}v + \frac{\partial I}{\partial t} = 0 \]

其中 $u = \frac{\Delta x}{\Delta t}$、$v = \frac{\Delta y}{\Delta t}$ 分别表示光流在水平和垂直方向的分量。由于这是一个包含两个未知数的单一方程，无法直接求解，因此需要引入额外约束条件。

HS 光流法详解

Horn-Schunck（简称 HS）方法是一种广泛应用的全局光流计算模型。它在原有约束基础上增加了光流场的平滑性假设，即相邻像素间的光流变化应尽可能连续和平缓。

为此，HS 方法构建了一个能量函数 $E$，由两部分构成：

• 数据项：衡量光流方程的拟合程度，表达式为： \[ E_d = \sum_{x,y}\left(\frac{\partial I}{\partial x}u + \frac{\partial I}{\partial y}v + \frac{\partial I}{\partial t}\right)^2 \]
• 平滑项：保证光流场的空间一致性，定义如下： \[ E_s = \alpha^2 \sum_{x,y} \left( \left(\frac{\partial u}{\partial x}\right)^2 + \left(\frac{\partial u}{\partial y}\right)^2 + \left(\frac{\partial v}{\partial x}\right)^2 + \left(\frac{\partial v}{\partial y}\right)^2 \right) \]

总能量函数为两者之和：

\[ E = E_d + E_s \]

通过变分法最小化该能量函数，可迭代求解出每个像素点的光流分量 $u$ 和 $v$，从而获得完整的光流场。

Matlab 程序实现流程

以下是一个基于 HS 光流法的简易 Matlab 实现框架，适用于任意运动目标检测任务，包括交通流、行人等视频内容。

1. 视频读取与初始化

首先加载待处理的视频文件，并获取总帧数以便后续逐帧处理：

videoFileReader = VideoReader('your_video_file.mp4');
numFrames = videoFileReader.NumberOfFrames;

VideoReader

该步骤利用 Matlab 内置的 VideoReader 类完成视频解析，确保兼容多种常见格式。

2. 光流参数设置

设定 HS 算法的关键参数：

alpha = 0.012;   % 平滑系数
nIter = 10;      % 迭代优化次数

alpha

参数 alpha 控制光流场的平滑程度——值越小，结果越平滑，但可能损失局部细节；nIter 决定迭代优化的轮数，影响精度与计算效率。

nIter

3. 帧间处理循环

对视频中的每一对连续帧执行光流计算：

for k = 1:numFrames - 1
    % 读取当前帧与下一帧
    frame1 = read(videoFileReader, k);
    frame2 = read(videoFileReader, k + 1);

    % 转换为灰度图像
    gray1 = rgb2gray(frame1);
    gray2 = rgb2gray(frame2);

    % （后续调用 HS 光流算法计算 u, v）
end

此循环结构实现了从原始彩色视频到灰度序列的转换，为光流计算做好准备。实际应用中可在内部集成自定义的 HS 光流求解模块，提取运动矢量场。

% 读取视频
videoFileReader = VideoReader('your_video_file.mp4');
numFrames = videoFileReader.NumberOfFrames;

% 初始化光流参数
alpha = 0.012; % 平滑参数
nIter = 10;    % 迭代次数

for k = 1:numFrames - 1
    % 读取当前帧和下一帧
    frame1 = read(videoFileReader, k);
    frame2 = read(videoFileReader, k + 1);
    
    % 将帧转换为灰度图
    gray1 = rgb2gray(frame1);
    gray2 = rgb2gray(frame2);
    
    % 计算图像梯度
    [Ix, Iy, It] = computeGradient(gray1, gray2);
    
    % 初始化光流
    u = zeros(size(gray1));
    v = zeros(size(gray1));
    
    for iter = 1:nIter
        % 计算光流的平滑项
        ux = imfilter(u, [-0.25 0 0.25], 'conv','replicate');
        uy = imfilter(u, [-0.25; 0; 0.25], 'conv','replicate');
        vx = imfilter(v, [-0.25 0 0.25], 'conv','replicate');
        vy = imfilter(v, [-0.25; 0; 0.25], 'conv','replicate');
        
        % 更新光流
        denominator = Ix.^2 + Iy.^2 + alpha^2 * (ux.^2 + uy.^2 + vx.^2 + vy.^2);
        u = (Iy.^2 * u - Ix.* Iy.* v - Ix.* It)./ denominator;
        v = (-Ix.* Iy.* u + Ix.^2 * v - Iy.* It)./ denominator;
    end
    
    % 这里可以根据光流结果进行运动目标检测相关操作，比如设定阈值筛选明显运动的区域
    % 简单可视化光流
    figure;
    imagesc(frame1);
    hold on;
    [X, Y] = meshgrid(1:size(u, 2), 1:size(u, 1));
    quiver(X, Y, u, v, 'r');
    hold off;
end

function [Ix, Iy, It] = computeGradient(im1, im2)
    % 使用高斯滤波器平滑图像
    im1 = imgaussfilt(im1, 1.5);
    im2 = imgaussfilt(im2, 1.5);
    
    % 计算x和y方向的梯度
    Ix = imfilter(im1, [-0.25 0 0.25], 'conv','replicate');
    Iy = imfilter(im1, [-0.25; 0; 0.25], 'conv','replicate');
    
    % 计算时间方向的梯度
    It = im2 - im1;
end

整个流程适用于各类动态场景的运动分析，具备良好的通用性和扩展性。

该算法通过逐帧读取视频数据，每次连续获取两帧图像（当前帧与下一帧），并将其转换为灰度图像。由于光流法通常在灰度空间中进行计算，这种处理方式既能有效降低计算复杂度，又不会丢失关键的运动信息。

gray2 = rgb2gray(frame2);

梯度计算函数实现

以下为用于计算图像空间和时间梯度的 MATLAB 函数：

function [Ix, Iy, It] = computeGradient(im1, im2)
% 使用高斯滤波对图像进行平滑处理
im1 = imgaussfilt(im1, 1.5);
im2 = imgaussfilt(im2, 1.5);

% 计算 x 和 y 方向的空间梯度
Ix = imfilter(im1, [-0.25 0 0.25], 'conv','replicate');
Iy = imfilter(im1, [-0.25; 0; 0.25], 'conv','replicate');



% 时间维度上的梯度由两帧图像相减得到
It = im2 - im1;
end

首先调用高斯滤波函数对输入图像进行预处理，以削弱噪声干扰。随后利用类似 Sobel 算子的卷积核模板，通过 imfilter 函数分别提取图像在水平和垂直方向的空间梯度分量。而时间方向的梯度则直接采用前后两帧灰度图之差来估算。

imgaussfilt

imfilter

光流场迭代更新过程

核心迭代部分依据 Horn-Schunck 模型的能量最小化原理，逐步优化光流场估计值：

for iter = 1:nIter
    % 计算光流场 u 和 v 在空间上的梯度（平滑项）
    ux = imfilter(u, [-0.25 0 0.25], 'conv','replicate');
    uy = imfilter(u, [-0.25; 0; 0.25], 'conv','replicate');
    vx = imfilter(v, [-0.25 0 0.25], 'conv','replicate');
    vy = imfilter(v, [-0.25; 0; 0.25], 'conv','replicate');

    % 更新光流向量 u 和 v
    denominator = Ix.^2 + Iy.^2 + alpha^2 * (ux.^2 + uy.^2 + vx.^2 + vy.^2);
    u = (Iy.^2 .* u - Ix .* Iy .* v - Ix .* It) ./ denominator;
    v = (-Ix .* Iy .* u + Ix.^2 .* v - Iy .* It) ./ denominator;
end

在每一次迭代中，系统首先对当前光流场 u 和 v 进行空间梯度计算，作为正则化平滑项。然后结合已知的图像梯度 Ix、Iy 和 It，按照 HS 模型的解析公式同步更新每个像素点的光流矢量，使整体能量函数趋于最小。

结果可视化方法

为了直观展示计算所得的光流场分布，程序使用如下代码进行图形绘制：

figure;
imagesc(frame1);
hold on;
[X, Y] = meshgrid(1:size(u, 2), 1:size(u, 1));
quiver(X, Y, u, v, 'r');
hold off;

该部分将第一帧图像作为背景显示，并利用 meshgrid 构建坐标网格，再通过 quiver 函数叠加绘制红色箭头，形象地表示各位置处的光流方向与大小。

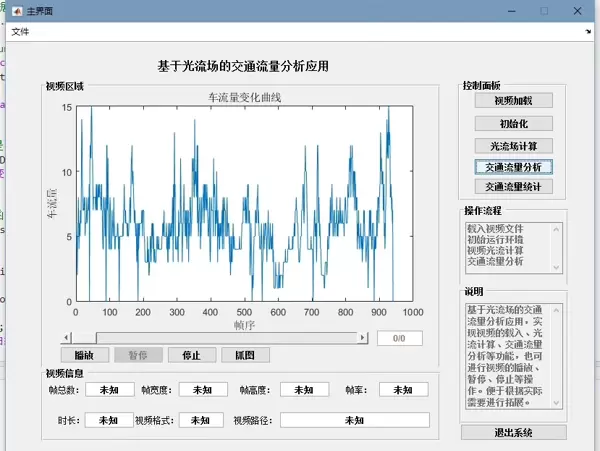
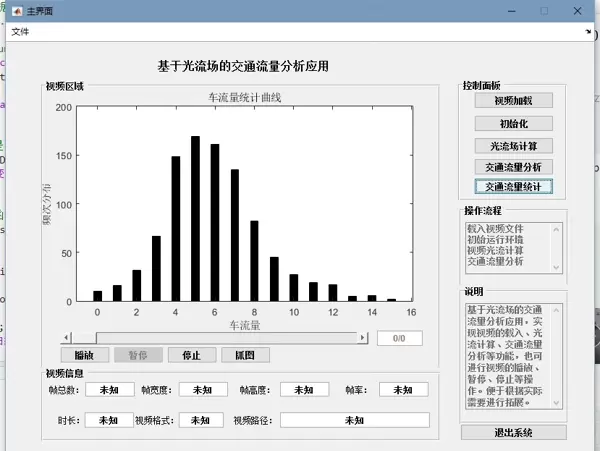
quiver

上述流程完整实现了基于 Horn-Schunck 光流法的运动分析框架，适用于多种动态场景视频，包括车流、人流等目标的运动检测。所构建的光流场不仅反映了物体移动趋势，也为后续智能交通系统的流量统计、行为识别等高级应用提供了可靠的数据支持。

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

分享0 收藏0 回帖

关键词：MATLAB matla atlab 交通流量 Mat

相关内容：Matlab交通流量分析