朴素贝叶斯实战：用Python实现西瓜分类器

是 否 +2 论坛币

k人 参与回答

经管之家送您一份

应届毕业生专属福利!

求职就业群

赵安豆老师微信：zhaoandou666

经管之家联合CDA

送您一个全额奖学金名额~ !

立即领取

感谢您参与论坛问题回答

经管之家送您两个论坛币！

+2 论坛币

1. 为什么选择朴素贝叶斯？引言

本文将带您完成一个基于朴素贝叶斯算法的机器学习实战项目——构建西瓜分类器，用于判断西瓜是好瓜还是坏瓜。那么，为何要选择朴素贝叶斯作为入门算法呢？原因如下：

• 原理清晰直观：算法建立在条件概率基础上，无需复杂的数学推导，易于理解。
• 计算高效：尤其适合小样本数据集，训练和预测速度都非常快。
• 应用广泛且实用：在文本分类、垃圾邮件识别等场景中表现优异。
• 鲁棒性强：即使特征之间并非完全独立，模型仍能取得不错的分类效果。

2. 项目目标与数据说明

2.1 数据集概况

本项目采用《机器学习》（周志华著）中的经典西瓜数据集，共包含17个已标注样本：

• 好瓜：8个样本
• 坏瓜：9个样本

每个样本包含8个特征，分为两类：

• 离散型特征（6个）：色泽、根蒂、敲声、纹理、脐部、触感
• 连续型特征（2个）：密度、含糖率

给定一个新西瓜的特征：
色泽=青绿，根蒂=蜷缩，敲声=浊响，纹理=清晰，
脐部=凹陷，触感=硬滑，密度=0.697，含糖率=0.460

预测这个西瓜是好瓜还是坏瓜？

2.2 问题定义

我们的任务是：根据给定的西瓜特征，判断其属于“好瓜”或“坏瓜”类别。这是一类典型的二分类问题，适用于朴素贝叶斯方法进行建模。

3. 算法核心：朴素贝叶斯理论基础

3.1 贝叶斯公式解析

朴素贝叶斯的核心依赖于贝叶斯定理，其数学表达式如下：

P(类别|特征) = P(特征|类别) × P(类别) ÷ P(特征)

其中各部分含义为：

• P(类别|特征)：后验概率，即在已知特征条件下属于某类别的概率，是我们最终需要求解的目标。
• P(特征|类别)：条件概率，表示在某个类别下观察到该特征的概率。
• P(类别)：先验概率，反映各类别在整体数据中的初始分布情况。
• P(特征)：证据因子，对所有类别下该特征出现的总概率进行归一化处理。

3.2 “朴素”的由来

所谓“朴素”，源于模型的一个强假设：所有特征之间相互独立。这意味着联合条件概率可以拆解为各个特征条件概率的乘积：

P(特征1,特征2,...,特征n|类别) = P(特征1|类别) × P(特征2|类别) × ... × P(特征n|类别)

尽管现实中这一假设往往不成立，但它极大简化了计算过程，使得模型在低资源环境下依然可用，并保持较高的分类性能。

4. 实现细节：从数据到预测

4.1 数据预处理

首先对原始数据进行结构化整理，提取特征并划分训练集。确保离散特征以类别形式存储，连续特征保留数值精度。

# 好瓜（是）的样本（8个）
good_melon = {
    '色泽': ['青绿', '乌黑', '乌黑', '青绿', '浅白', '青绿', '乌黑', '乌黑'],
    '根蒂': ['蜷缩', '蜷缩', '蜷缩', '蜷缩', '蜷缩', '稍蜷', '稍蜷', '稍蜷'],
    # ... 其他特征类似
    '密度': [0.697, 0.774, 0.634, 0.608, 0.556, 0.403, 0.481, 0.437],
    '含糖率': [0.460, 0.376, 0.264, 0.318, 0.215, 0.237, 0.149, 0.211]
}

4.2 离散特征处理：拉普拉斯平滑

直接统计频率可能导致某些未出现的特征组合概率为0，从而影响整体预测。为解决此问题，引入拉普拉斯平滑技术：

def discrete_prob(feature, value, data, total_samples):
    count = feature_values.count(value)  # 统计出现次数
    # 关键：分子+1，分母+特征的可能取值数
    prob = (count + 1) / (total_samples + 2)
    return prob

具体操作：

• 分子加1：防止任何条件概率为零
• 分母加上该特征可能取值的数量：保证调整后的概率总和仍为1

4.3 连续特征建模：正态分布假设

对于密度和含糖率这类连续变量，无法使用频数统计。我们假设它们在每一类别下服从正态分布：

def continuous_prob(feature, value, data):
    values = data[feature]
    mean = np.mean(values)      # 计算均值
    std = np.std(values, ddof=1)  # 计算标准差
    prob = norm.pdf(value, loc=mean, scale=std)  # 正态分布概率密度
    return prob

注意：

• 这里计算的是概率密度值，而非概率本身
• 使用最大似然估计法估算均值与方差

pdf

prob

4.4 后验概率计算流程

综合离散与连续特征，分别计算属于“好瓜”和“坏瓜”的后验概率（省略分母项），然后比较大小得出分类结果。

# 步骤1：计算先验概率
p_good = 8 / 17  # 好瓜的概率
p_bad = 9 / 17   # 坏瓜的概率

# 步骤2：计算条件概率乘积（"朴素"的体现）
p_feature_good = 1.0
for feat in ['色泽', '根蒂', '敲声', '纹理', '脐部', '触感']:
    p_feature_good *= discrete_prob(feat, test_sample[feat], good_melon, 8)
# 乘以连续特征的概率密度
p_feature_good *= continuous_prob('密度', test_sample['密度'], good_melon)
p_feature_good *= continuous_prob('含糖率', test_sample['含糖率'], good_melon)

# 步骤3：计算后验概率（正比于）
p_good_final = p_good * p_feature_good

5. 结果展示与分析

运行完整代码后，得到如下输出：

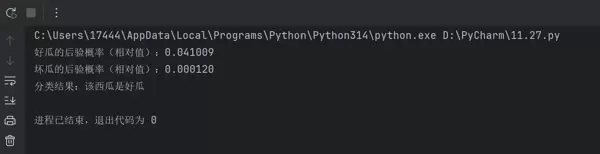
结果解读：

• 为何是相对值？ 因为我们忽略了相同的分母项

  P(特征)

  ，仅需比较分子即可确定类别归属。
• 为何好瓜概率显著更高？ 测试样本的多个离散特征（如色泽、纹理等）在好瓜类别中频繁出现，匹配度高。
• 分类是否正确？ 是的！该测试样本正是训练集中第一个被标记为“好瓜”的实例。

6. 可能的问题与优化方向

6.1 存在的局限性

• 连续特征未必符合正态分布
• 特征独立性假设在实际中较难满足
• 拉普拉斯平滑中，不同特征的取值数量可能差异较大，简单加常数可能不够精确

6.2 潜在改进策略

可通过以下方式提升模型性能：

• 使用更灵活的概率密度估计方法（如核密度估计）替代正态假设
• 引入半朴素贝叶斯模型，允许部分特征间存在依赖关系
• 采用更精细的平滑策略（如加λ平滑）

# 改进1：更准确的离散特征取值统计
def get_feature_values(data, feature):
    """统计某个特征所有可能的取值"""
    return set(data[feature])

# 改进2：核密度估计替代正态分布
from scipy.stats import gaussian_kde
def kde_prob(value, data):
    kde = gaussian_kde(data)  # 核密度估计
    return kde.evaluate(value)[0]

7. 总结

通过本次实践，我们深入掌握了朴素贝叶斯算法的关键知识点：

• 基本原理：基于贝叶斯公式与特征独立假设进行概率推理
• 特征处理技巧：
  • 离散特征 → 使用拉普拉斯平滑避免零概率
  • 连续特征 → 假设服从正态分布并计算概率密度
• 全流程实现能力：涵盖数据准备、特征处理、概率计算到最终预测
• 优势总结：
  • 实现简单，运行效率高
  • 对小规模数据适应性强
  • 对缺失值具有一定的容忍性
• 主要局限：
  • 特征独立假设可能不符合现实
  • 需要合理设定先验概率

import numpy as np
from scipy.stats import norm  # 正态分布概率密度

# ---------------------- 1. 训练数据整理 ----------------------
# 好瓜（是）的样本（8个）
good_melon = {
    '色泽': ['青绿', '乌黑', '乌黑', '青绿', '浅白', '青绿', '乌黑', '乌黑'],
    '根蒂': ['蜷缩', '蜷缩', '蜷缩', '蜷缩', '蜷缩', '稍蜷', '稍蜷', '稍蜷'],
    '敲声': ['浊响', '沉闷', '浊响', '沉闷', '浊响', '浊响', '浊响', '浊响'],
    '纹理': ['清晰', '清晰', '清晰', '清晰', '清晰', '清晰', '稍糊', '清晰'],
    '脐部': ['凹陷', '凹陷', '凹陷', '凹陷', '凹陷', '稍凹', '稍凹', '稍凹'],
    '触感': ['硬滑', '硬滑', '硬滑', '硬滑', '硬滑', '软粘', '软粘', '硬滑'],
    '密度': [0.697, 0.774, 0.634, 0.608, 0.556, 0.403, 0.481, 0.437],
    '含糖率': [0.460, 0.376, 0.264, 0.318, 0.215, 0.237, 0.149, 0.211]
}

# 坏瓜（否）的样本（9个）
bad_melon = {
    '色泽': ['乌黑', '青绿', '浅白', '浅白', '青绿', '浅白', '乌黑', '浅白', '青绿'],
    '根蒂': ['稍蜷', '硬挺', '硬挺', '蜷缩', '稍蜷', '稍蜷', '稍蜷', '蜷缩', '蜷缩'],
    '敲声': ['沉闷', '清脆', '清脆', '浊响', '浊响', '沉闷', '浊响', '浊响', '沉闷'],
    '纹理': ['稍糊', '清晰', '模糊', '模糊', '稍糊', '稍糊', '清晰', '模糊', '稍糊'],
    '脐部': ['稍凹', '平坦', '平坦', '平坦', '凹陷', '凹陷', '稍凹', '平坦', '稍凹'],
    '触感': ['硬滑', '软粘', '硬滑', '软粘', '硬滑', '硬滑', '软粘', '硬滑', '硬滑'],
    '密度': [0.666, 0.243, 0.245, 0.343, 0.639, 0.657, 0.360, 0.593, 0.719],
    '含糖率': [0.091, 0.267, 0.057, 0.099, 0.161, 0.198, 0.370, 0.042, 0.103]
}

# 测试样本（测1）
test_sample = {
    '色泽': '青绿',
    '根蒂': '蜷缩',
    '敲声': '浊响',
    '纹理': '清晰',
    '脐部': '凹陷',
    '触感': '硬滑',
    '密度': 0.697,
    '含糖率': 0.460
}


# ---------------------- 2. 计算离散特征的条件概率（拉普拉斯平滑） ----------------------
def discrete_prob(feature, value, data, total_samples):
    """
    计算离散特征的条件概率（拉普拉斯平滑）
    feature: 特征名（如'色泽'）
    value: 特征值（如'青绿'）
    data: 对应类别（好/坏瓜）的特征数据
    total_samples: 对应类别的样本总数
    """
    feature_values = data[feature]
    count = feature_values.count(value)
    # 拉普拉斯平滑：分子+1，分母+特征的可能取值数（这里简化为2，实际需统计所有可能值）
    prob = (count + 1) / (total_samples + 2)
    return prob


# ---------------------- 3. 计算连续特征的概率密度（正态分布） ----------------------
def continuous_prob(feature, value, data):
    """
    计算连续特征的概率密度（假设服从正态分布）
    feature: 特征名（如'密度'）
    value: 特征值（如0.697）
    data: 对应类别（好/坏瓜）的特征数据
    """
    values = data[feature]
    mean = np.mean(values)
    std = np.std(values, ddof=1)  # 样本标准差（无偏）
    prob = norm.pdf(value, loc=mean, scale=std)  # 正态分布概率密度
    return prob


# ---------------------- 4. 计算后验概率 ----------------------
# 先验概率（好瓜8个，坏瓜9个，总样本17个）
p_good = 8 / 17
p_bad = 9 / 17

# 计算“好瓜”的条件概率乘积
p_feature_good = 1.0
# 离散特征
for feat in ['色泽', '根蒂', '敲声', '纹理', '脐部', '触感']:
    p_feature_good *= discrete_prob(feat, test_sample[feat], good_melon, 8)
# 连续特征
p_feature_good *= continuous_prob('密度', test_sample['密度'], good_melon)
p_feature_good *= continuous_prob('含糖率', test_sample['含糖率'], good_melon)
# 好瓜的后验概率（正比于 p(是) * p(特征|是)）
p_good_final = p_good * p_feature_good


# 计算“坏瓜”的条件概率乘积
p_feature_bad = 1.0
# 离散特征
for feat in ['色泽', '根蒂', '敲声', '纹理', '脐部', '触感']:
    p_feature_bad *= discrete_prob(feat, test_sample[feat], bad_melon, 9)
# 连续特征
p_feature_bad *= continuous_prob('密度', test_sample['密度'], bad_melon)
p_feature_bad *= continuous_prob('含糖率', test_sample['含糖率'], bad_melon)
# 坏瓜的后验概率（正比于 p(否) * p(特征|否)）
p_bad_final = p_bad * p_feature_bad


# ---------------------- 5. 输出结果 ----------------------
print(f"好瓜的后验概率（相对值）：{p_good_final:.6f}")
print(f"坏瓜的后验概率（相对值）：{p_bad_final:.6f}")
if p_good_final > p_bad_final:
    print("分类结果：该西瓜是好瓜")
else:
    print("分类结果：该西瓜是坏瓜")

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

分享0 收藏0 回帖

关键词：python 朴素贝叶斯 贝叶斯 分类器 Continuous

相关内容：朴素贝叶斯西瓜分类实现