Guest post by Gergely Daróczi. If you like this content, you can buy the full 396 paged e-book for 5 USD until January 8, 2016 as part of Packt’s “$5 Skill Up Campaign” athttp://bit.ly/mastering-R
Feature extraction tends to be one of the most important steps in machine learning and data science projects, so I decided to republish a related short section from my intermediate book on how to analyze data with R. The 9th chapter is dedicated to traditional dimension reduction methods, such as Principal Component Analysis, Factor Analysis and Multidimensional Scaling — from which the below introductory examples will focus on that latter.
Multidimensional Scaling (MDS) is a multivariate statistical technique first used in geography. The main goal of MDS it is to plot multivariate data points in two dimensions, thus revealing the structure of the dataset by visualizing the relative distance of the observations. Multidimensional scaling is used in diverse fields such as attitude study in psychology, sociology or market research.
Although the MASS package provides non-metric methods via the isoMDS function, we will now concentrate on the classical, metric MDS, which is available by calling the cmdscale function bundled with the stats package. Both types of MDS take a distance matrix as the main argument, which can be created from any numeric tabular data by the dist function.
But before such more complex examples, let’s see what MDS can offer for us while working with an already existing distance matrix, like the built-in eurodist dataset:
> as.matrix(eurodist)[1:5, 1:5] Athens Barcelona Brussels Calais CherbourgAthens 0 3313 2963 3175 3339Barcelona 3313 0 1318 1326 1294Brussels 2963 1318 0 204 583Calais 3175 1326 204 0 460Cherbourg 3339 1294 583 460 0The above subset (first 5-5 values) of the distance matrix represents the travel distance between 21 European cities in kilometers. Running classical MDS on this example returns:
> (mds <- cmdscale(eurodist)) [,1] [,2]Athens 2290.2747 1798.803Barcelona -825.3828 546.811Brussels 59.1833 -367.081Calais -82.8460 -429.915Cherbourg -352.4994 -290.908Cologne 293.6896 -405.312Copenhagen 681.9315 -1108.645Geneva -9.4234 240.406Gibraltar -2048.4491 642.459Hamburg 561.1090 -773.369Hook of Holland 164.9218 -549.367Lisbon -1935.0408 49.125Lyons -226.4232 187.088Madrid -1423.3537 305.875Marseilles -299.4987 388.807Milan 260.8780 416.674Munich 587.6757 81.182Paris -156.8363 -211.139Rome 709.4133 1109.367Stockholm 839.4459 -1836.791Vienna 911.2305 205.930These scores are very similar to two principal components (discussed in the previous, Principal Component Analysis section), such as running prcomp(eurodist)$x[, 1:2]. As a matter of fact, PCA can be considered as the most basic MDS solution.
Anyway, we have just transformed (reduced) the 21-dimensional space into 2 dimensions, which can be plotted very easily — unlike the original distance matrix with 21 rows and 21 columns:
> plot(mds)[color=rgb(255, 255, 255) !important]
Does it ring a bell? If not yet, the below image might be more helpful, where the following two lines of code also renders the city names instead of showing anonymous points:
> plot(mds, type = 'n')> text(mds[, 1], mds[, 2], labels(eurodist))[color=rgb(255, 255, 255) !important]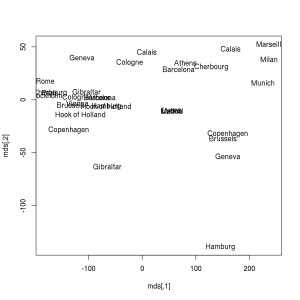
Although the y axis seems to be flipped (which you can fix by multiplying the second argument of text by-1), but we have just rendered a map of some European cities from the distance matrix — without any further geographical data. I hope you find this rather impressive!
Please find more data visualization tricks and methods in the 13th, Data Around Us chapter, from which you can learn for example how to plot the above results over a satellite map downloaded from online service providers. For now, I will only focus on how to render this plot with the new version of ggplot2to avoid overlaps in the city names, and suppressing the not that useful x andy axis labels and ticks:
> library(ggplot2)> ggplot(as.data.frame(mds), aes(V1, -V2, label = rownames(mds))) ++ geom_text(check_overlap = TRUE) + theme_minimal() + xlab('') + ylab('') ++ scale_y_continuous(breaks = NULL) + scale_x_continuous(breaks = NULL)[color=rgb(255, 255, 255) !important]
But let’s get back to the original topic and see how to apply MDS on non-geographic data, which was not prepared to be a distance matrix. We will use the mtcars dataset in the following example resulting in a plot with no axis elements:
> mds <- cmdscale(dist(mtcars))> plot(mds, type = 'n', axes = FALSE, xlab = '', ylab = '')> text(mds[, 1], mds[, 2], rownames(mds))[color=rgb(255, 255, 255) !important]
The above plot shows the 32 cars of the original dataset scattered in a two dimensional space. The distance between the elements was computed by MDS, which took into account all the 11 original numeric variables, and it makes vert easy to identify the similar and very different car types. We will cover these topics in more details in the next chapter, which is dedicated toClassification and Clustering.
This article first appeared in the “Mastering Data Analysis with R” book, and is now published with the permission of Packt Publishing.
To leave a comment for the author, please follow the link and comment on their blog: R – R-statistics blog.
R-bloggers.com offers daily e-mail updates about R news and tutorials on topics such as: Data science, Big Data,R jobs, visualization (ggplot2, Boxplots, maps, animation), programming (RStudio, Sweave, LaTeX, SQL,Eclipse, git, hadoop, Web Scraping) statistics (regression, PCA, time series, trading) and more...




 雷达卡
雷达卡

















 京公网安备 11010802022788号
京公网安备 11010802022788号







