- 阅读权限
- 255
- 威望
- 0 级
- 论坛币
- 57 个
- 通用积分
- 6.2197
- 学术水平
- 0 点
- 热心指数
- 0 点
- 信用等级
- 0 点
- 经验
- 1122 点
- 帖子
- 75
- 精华
- 0
- 在线时间
- 474 小时
- 注册时间
- 2011-12-10
- 最后登录
- 2025-12-28
博士生
还不是VIP/贵宾
- 威望
- 0 级
- 论坛币
 - 57 个
- 通用积分
- 6.2197
- 学术水平
- 0 点
- 热心指数
- 0 点
- 信用等级
- 0 点
- 经验
- 1122 点
- 帖子
- 75
- 精华
- 0
- 在线时间
- 474 小时
- 注册时间
- 2011-12-10
- 最后登录
- 2025-12-28
 | 开心 2022-1-7 19:40:23 |
|---|
签到天数: 178 天 连续签到: 1 天 [LV.7]常住居民III |
经管之家送您一份
应届毕业生专属福利!
 求职就业群
求职就业群
感谢您参与论坛问题回答
经管之家送您两个论坛币!
+2 论坛币
R语言非线性回归入门作者 Lionel Hertzog 在一簇散点中拟合一条回归线(即线性回归)是数据分析的基本方法之一。有时,线性模型能很好地拟合数据,但在某些(很多)情形下,变量间的关系未必是线性的。这时,一般有三类方法解决这个问题: (1) 通过变换数据使得其关系线性化, (2) 用多项式或者比较复杂的样条来拟合数据, (3) 用非线性函数来拟合数据从标题你应该已经猜到非线性回归是本文的重点什么是非线性回归在非线性回归中,分析师通常采用一个确定的函数形式和相应的参数来拟合数据。最常用的参数估计方法是利用非线性最小二乘法(R中的nls函数)。该方法使用线性函数来逼近非线性函数,并且通过不断迭代这个过程来得到参数的最优解(本段来自维基百科)。非线性回归的良好性质之一是估计出的参数都有清晰的解释(如Michaelis-Menten模型的Vmax是指最大速率),而变换数据后得到的线性模型其参数往往难以解释。非线性最小二乘拟合首先,我们以Michaelis-Menten方程为例。# 生成一些仿真数据set.seed(20160227) x <- seq(0, 50, 1)y <- ((runif(1, 10, 20)*x)/(runif(1, 0, 10)+x)) + rnorm(51, 0, 1)# 对于一些简单的模型,nls函数可以自动找到合适的参数初值m <- nls(y ~ a*x/(b+x))# 计算模型的拟合优度cor(y, predict(m))[1 0.9496598# 将结果可视化plot(x, y) lines(x, predict(m), lty = 2, col = "red", lwd = 3)输出的图片如下:
选择适宜的迭代初值在非线性回归中,找到合适的迭代初值对于整个模型算法的收敛性而言至关重要。假如你设定的参数初值完全脱离了其潜在的取值范围,迭代算法可能不收敛或者返回一些没有意义的参数值。比如返回一个大小为1000的增长率,但其真值却是1.04。寻找合适初值的最好办法是“紧盯着”数据,绘制相应图表并结合你对方程的理解来确定参数的合适初值。# 生成仿真数据,并且此次对于参数没有先验信息y <- runif(1, 5, 15)*exp(-runif(1, 0.01, 0.05)*x)+rnorm(51, 0, 0.5)# 可视化数据并选择一些参数初值plot(x, y)# 通过这个散点图确定参数a, b的初值a_start <- 8 # 参数a是x = 0时y的取值b_start<- 2*log(2)/a_start # b 是衰减速率# 拟合模型m <- nls(y ~ a*exp(-b*x), start = list(a = a_start, b = b_start))# 计算拟合优度cor(y, predict(m))[1 0.9811831# 将结果可视化lines(x, predict(m), col = "red", lty = 2, lwd = 3)输出的图片如下
使用自启动函数不同的科学研究领域会对同一个模型设定不同的参数形式(即不同的方程),比如研究人口增长的逻辑斯蒂模型,在生态学中一般采用如下形式: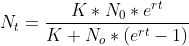
等式中的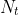 代表时间t时的个体数, 代表时间t时的个体数, 是个体增长速率, 是个体增长速率,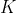 是环境承载能力。我们可以将这个等式改写为微分方程的形式: 是环境承载能力。我们可以将这个等式改写为微分方程的形式: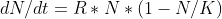
library(deSolve)# 利用逻辑斯蒂模型生成人口增长的仿真数据,并用nls估计参数log_growth <- function(Time, State, Pars) { with(as.list(c(State, Pars)), { dN <- R*N*(1-N/K) return(list(c(dN))) })}# 逻辑斯蒂增长的参数pars <- c(R = 0.2, K = 1000)# 设定初值N_ini <- c(N = 1)# 常微分方程的时间阶段(下标t)times <- seq(0, 50, by = 1)# 常微分方程out <- ode(N_ini, times, log_growth, pars)# 添加一些随机波动N_obs <- out[, 2]+rnorm(51, 0, 50)# 个体数值不能小于1N_obs <- ifelse(N_obs<1, 1, N_obs)# 画图plot(times, N_obs)这部分代码只是生成了带有随机误差的仿真数据,接下来的部分会展现估计参数初值的技巧。R语言中有一个估计逻辑斯蒂方程参数的内建函数(SSlogis),但它使用的是如下方程: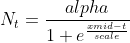
# 寻找方程的参数SS <- getInitial(N_obs ~ SSlogis(times, alpha, xmid, scale), data = data.frame(N_obs = N_obs, times = times))我们可使用getInitial函数来对模型参数做一个基于数据的初步估计。然后把该函数的输出作为一个向量化参数传递给自启动函数(SSlogis),同时也将无引号的三个参数名赋值给逻辑斯蒂方程(译者注:即alpha,xmid,scale三个参数)。然而,由于SSlogis的参数设定有些不同,我们需要对SSlogis的输出值做一些处理,使得其与逻辑斯蒂方程中的形式一致。
输出图形如下:
修改SSlogis输出的参数结构确实有些繁琐,不过值得一试。在后续的文章中,除了非线性最小二乘法,我们将利用更为可靠和强大的极大似然估计法来拟合模型。它能使你构建你能想到的任何模型。
![二维码]()
扫码加我 拉你入群
请注明:姓名-公司-职位
以便审核进群资格,未注明则拒绝
|
|
|


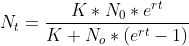
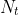 代表时间t时的个体数,
代表时间t时的个体数, 是个体增长速率,
是个体增长速率,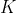 是环境承载能力。我们可以将这个等式改写为微分方程的形式:
是环境承载能力。我们可以将这个等式改写为微分方程的形式: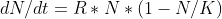
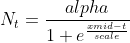

 加好友,备注cda
加好友,备注cda 京公网安备 11010802022788号
论坛法律顾问:王进律师
知识产权保护声明
免责及隐私声明
京公网安备 11010802022788号
论坛法律顾问:王进律师
知识产权保护声明
免责及隐私声明





