python机器学习: lasso回归

是 否 +2 论坛币

k人 参与回答

经管之家送您一份

应届毕业生专属福利!

求职就业群

赵安豆老师微信：zhaoandou666

经管之家联合CDA

送您一个全额奖学金名额~ !

立即领取

感谢您参与论坛问题回答

经管之家送您两个论坛币！

+2 论坛币

CDA数据分析师：数据科学、人工智能从业者的在线大学。
数据科学（Python/R/Julia）数据分析、机器学习、深度学习

上节我们介绍了线性回归和Ridge回归，并介绍了两种回归的优缺点。本节我们重点学习下lasso回归的方法和优缺点。

和岭回归（Ridge）回归一样，lasso回归也是一种正则化的线性回归，且也是约束系数使其接近于0，不过其用到的方法不同，岭回归用到的是L2正则化，而lasso回归用到的是L1正则化（L1是通过稀疏参数（减少参数的数量）来降低复杂度，即L1正则化使参数为零，L2是通过减小参数值的大小来降低复杂度，即L2正则化项使得值最小时对应的参数变小）。

下面我们来看将lasso正则化运用到波士顿房价数据集上的效果，对应代码如下：

1. import mglearn
   
2. 
   
3. from sklearn.model_selection import train_test_split
   
4. 
   
5. import matplotlib.pyplot as plt
   
6. 
   
7. x, y = mglearn.datasets.load_extended_boston
   
8. 
   
9. x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=0)
   
10. 
    
11. from sklearn.linear_model import Lasso
    
12. 
    
13. lasso = Lasso.fit(x_train, y_train)
    
14. 
    
15. print("Training set score: {:.2f}".format(lasso.score(x_train, y_train)))
    
16. 
    
17. print("Test set score: {:.2f}".format(lasso.score(x_test, y_test)))
    
18. 
    
19. print("Number of features used: {}".format(np.sum(lasso.coef_!=0)))
    
20. 
    
21. #我们增大max_iter的值，否则模型会警告我们，应该增大max_iter
    
22. 
    
23. #下面代码则是打印各种alpha参数下的预测分数
    
24. 
    
25. lasso01 = Lasso(alpha=0.1, max_iter=100000).fit(x_train, y_train)
    
26. 
    
27. lasso001 = Lasso(alpha=0.01, max_iter=100000).fit(x_train, y_train)
    
28. 
    
29. print("training set score: {:.2f}".format(lasso001.score(x_train, y_train)))
    
30. 
    
31. print("Test set score: {:.2f}".format(lasso001.score(x_test, y_test)))
    
32. 
    
33. print("Number of features used: {}".format(np.sum(lasso001.coef_!=0)))
    
34. 
    
35. lasso00001 = Lasso(alpha=0.0001, max_iter=100000).fit(x_train, y_train)
    
36. 
    
37. print("training set score: {:.2f}".format(lasso00001.score(x_train, y_train)))
    
38. 
    
39. print("Test set score: {:.2f}".format(lasso00001.score(x_test, y_test)))
    
40. 
    
41. print("Number of features used: {}".format(np.sum(lasso00001.coef_!=0)))
    
42. 
    
43. #绘制对应的图形
    
44. 
    
45. plt.plot(lasso.coef_, 's', label="Lasso alpha=1")
    
46. 
    
47. plt.plot(lasso001.coef_, '^', label="Lasso alpha=0.01")
    
48. 
    
49. plt.plot(lasso00001.coef_, 'v', label="Lasso alpha=0.0001")
    
50. 
    
51. plt.plot(lasso01.coef_, 'v', label="Ridge alpha=0.1")
    
52. 
    
53. plt.legend(ncol=2, loc=(0, 1.05))
    
54. 
    
55. plt.ylim(-25, 25)
    
56. 
    
57. plt.xlabel("Coefficient index")
    
58. 
    
59. plt.ylabel("Cofficient magnitude")

复制代码

上述代码运行结果如下：

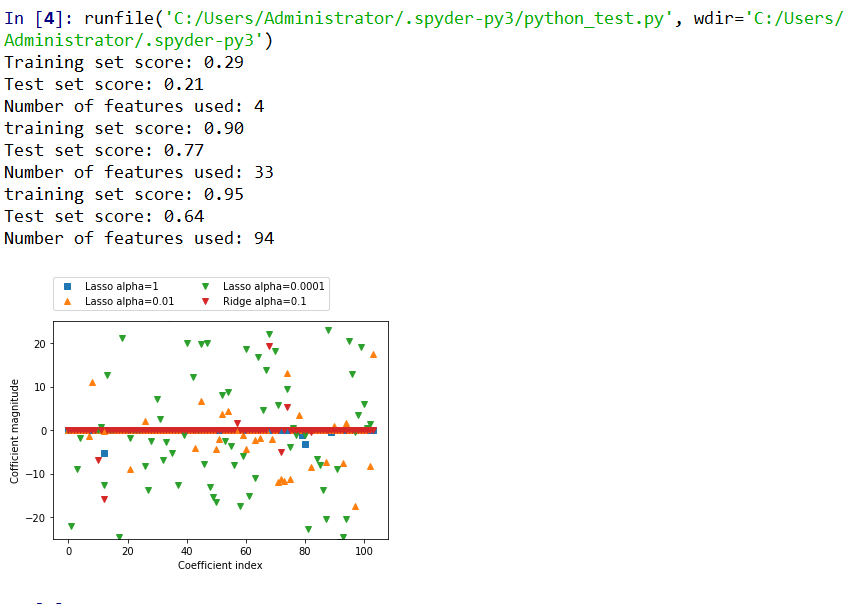
不同alpha值得lasso和岭回归（ridge）的系数比较

由上述代码我们可以看出，当使用特征数比较少时，lasso的训练集和测试集表现都很差，这表示存在欠拟合。通过调整alpha值，可以控制系数趋向于0的强度。当我们将alpha值变小，我们可以拟合一个比较复杂的模型，此时，训练集和测试集反而表现得更好，当我们将特征值从4个上升到33个是，训练集和测试集已经表现得比较好了。不过，如果将alpha值设置得太小的时候，训练集就会远大于测试集了，这是就出现了过拟合的情况。

在实践中，岭回归（Ridge）和lasso我们首选岭回归。不过如果特征数过多，但是其中只有几个特征是重要的，则选择lasso效果会更好。同时，lasso由于其模型更加便于理解（因为它只选择一部分输入特征），所以有时候用lasso回归效果也不错。当然，如果我们能够将两者进行优势互补，则会达到更佳的效果，在scikit-learn中提过了ElasticNet类，就是结合了这两种回归的惩罚项。在实践中效果会更好，不过需要同时调节L1和L2正则化参数，在以后章节中我们会介绍到。

扫码加我 拉你入群

请注明：姓名-公司-职位

以便审核进群资格，未注明则拒绝

分享0 收藏1 回帖

关键词：python LASSO 机器学习 scikit-learn coefficient

谢谢好贴！